A Semi-supervised Graph Attentive Network for Financial Fraud Detection 个人总结
A Semi-supervised Graph Attentive Network for Financial Fraud Detection 个人总结
写在前面:为方便阅读,尽量使用中文总结,对于翻译无把握或专有词汇,在中文后附上原文字段。此外,水平有限,对文章理解有偏差部分恳请大家海涵, 指正。
顺便,移步去GitHub看看憋>﹏<
0. 原作信息
@inproceedings{wang2019semi,
title={A Semi-supervised Graph Attentive Network for Financial Fraud Detection},
author={Wang, Daixin and Lin, Jianbin and Cui, Peng and Jia, Quanhui and Wang, Zhen and Fang, Yanming and Yu, Quan and Zhou, Jun and Yang, Shuang and Qi, Yuan},
booktitle={2019 IEEE International Conference on Data Mining (ICDM)},
pages={598--607},
year={2019},
organization={IEEE}
}
1. Contribution 本文贡献
-
设计semi-supervised GNN,利用有标签、无标签数据。(通过设计不同 L o s s Loss Loss实现)
-
使用Hieranchical Attention,增加模型可解释性
-
在花呗的异构数据上很work。
2. Background 背景信息
-
任务: 欺诈检测,Fraud Detection
可视作分类任务,由于异常点的采集,标注极其耗费人力物力,数据集常为少量有标签数据(labeled data),及大量无标签数据(unlabeled data).
模型需要具备解释性, 能向部署方, 被检测者说明检测的判别标准.
-
过往检测方式
- 基于规则, Rule-based
- 原理: 假定欺诈活动基于一定可观测的模式
- 缺点: 耗费人力手工设定, 依赖专家知识; 容易被攻击
- 基于统计特征的机器学习模型
- 如SVM, 树模型等
- 缺点: 未利用用户间交互信息
- 图表示学习的尝试
- 黑箱模型,缺乏解释性
- 基于规则, Rule-based
-
综上,欺诈检测建模有如下灵魂三问:
- 如何处理不平衡的数据,利用无标签的数据? (semi-supervised)
- 如何利用用户间交互,及不同类别的特征? (heterogenous graph)
- 如何保证模型可解释性?
3. The Model Semi-GNN 模型
3.1 Problem Definition and Notations 问题定义及注记
-
图的构建
- 重点研究User用户类型节点, 图中有标签数据<<无标签数据
- 异构图(文中记为multiview graph), G v = { U ∪ S v , E v } , v ∈ { 1 , … , m } G^{v}=\left\{U \cup S^{v}, E^{v}\right\}, v \in\{1, \ldots, m\} Gv={U∪Sv,Ev},v∈{1,…,m}, v v v即view
- view由具体业务确定, 本文中部分view是从用户特征处理产生的, 以增加结构信息. (详见实验部分数据集处理)
-
注记:
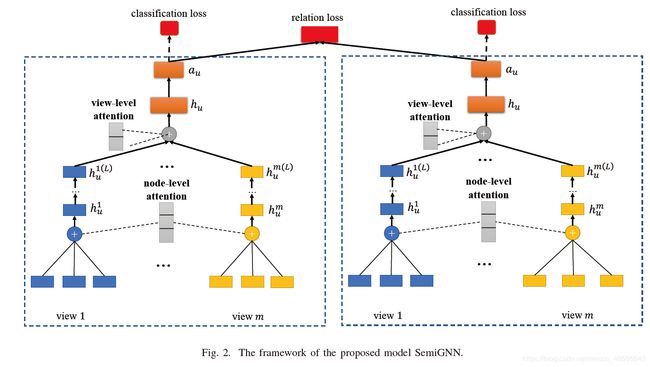
3.2 Overview 整体架构
node level(聚合各view内信息) → view level(整合views信息,得到对user的embedding) → relation loss ( 对有/无标签数据不同损失)
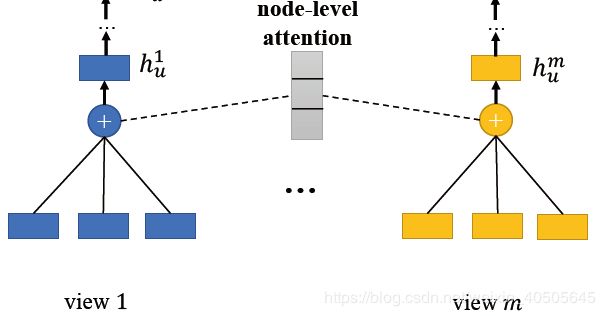
3.3 Node Level
对于节点u, i在view v中的特征表示, 设为 e u i v e_{u i}^{v} euiv
∵ 不同邻居节点对节点u的影响不同, 引入Attention来自主学习邻居节点的权重,
α u i v = exp ( e u i v ⋅ H u i v ) ∑ k ∈ N u v exp ( e u k v ⋅ H u k v ) \alpha_{u i}^{v}=\frac{\exp \left(e_{u i}^{v} \cdot H_{u i}^{v}\right)}{\sum_{k \in \mathcal{N}_{u}^{v}} \exp \left(e_{u k}^{v} \cdot H_{u k}^{v}\right)} αuiv=∑k∈Nuvexp(eukv⋅Hukv)exp(euiv⋅Huiv), 其中 H u v H^v_u Huv为可学习的参数矩阵.
∴ 对于节点u在viewv下的embedding,有:
h u v = ∑ k ∈ N u ( A ) α u k e u k h_{u}^{v}=\sum_{k \in \mathcal{N}_{u}^{(A)}} \alpha_{u k} e_{u k} huv=∑k∈Nu(A)αukeuk
3.4 View Level
-
MLP
个人理解即预处理, 但用MLP来映射总觉得有点偏, em, intuition?
由node-level得到的 h v u h^u_v hvu是属于各自view内(异构)的embedding, 为了聚合各个view时能更好的利用相互关联性(capture the multiview correlations), 首先用MLP将之映射到高维的语义空间(high-level semantic space).
即有,
h u v ( l ) = Relu ( h u v ( l − 1 ) W l v + b l v ) , v ∈ { 2 , … , m } h_{u}^{v(l)}=\operatorname{Relu}\left(h_{u}^{v(l-1)} W_{l}^{v}+b_{l}^{v}\right), v \in\{2, \ldots, m\} huv(l)=Relu(huv(l−1)Wlv+blv),v∈{2,…,m} -
View-Attention
不同view对User的embedding影响也不同,同样,引入Attention来自适应.
α u v = exp ( h u v ( L ) ⋅ ϕ u v ) ∑ k ∈ { 1 , … , m } exp ( h u k ( L ) ⋅ ϕ u k ) , v ∈ { 1 , … , m } \alpha_{u}^{v}=\frac{\exp \left(h_{u}^{v(L)} \cdot \phi_{u}^{v}\right)}{\sum_{k \in\{1, \ldots, m\}} \exp \left(h_{u}^{k(L)} \cdot \phi_{u}^{k}\right)}, v \in\{1, \ldots, m\} αuv=∑k∈{1,…,m}exp(huk(L)⋅ϕuk)exp(huv(L)⋅ϕuv),v∈{1,…,m}
最后, 连接在attention加权后各view节点表示,得到User的embedding.
h u = ∥ i = 1 m ( α u v ⋅ h u v ( L ) ) h_{u}=\|_{i=1}^{m}\left(\alpha_{u}^{v} \cdot h_{u}^{v(L)}\right) hu=∥i=1m(αuv⋅huv(L))
m为view个数,||为连接.
3.5 Loss 损失函数设计
- 标签数据
使用softmax
-
无标签数据
现象: 欺诈常呈团伙聚集, 标注为负样本的用户, 其邻居节点也可疑.
基于上述假设, 受DeepWalk启发, 作者设计的Loss希望:
邻近节点的表示是相似的, 同时不同节点的表示差异较大. (encourages nearby nodes having similar representaions while makes the representations of disparate nodes distinct)
听起来, 和聚类的要求是一致的, 更替了表述而已. 但为了实现上述期望, Loss的设计还是相当巧妙的.
↓↓↓
L graph = ∑ u ∈ U ∑ v ∈ N u ∪ N e g u − log ( σ ( a u T a v ) ) − Q ⋅ E q ∼ P n e g ( u ) log ( σ ( a u T a q ) ) \begin{aligned} \mathcal{L}_{\text {graph}}=& \sum_{u \in U} \sum_{v \in \mathcal{N}_{u} \cup N e g_{u}}-\log \left(\sigma\left(a_{u}^{T} a_{v}\right)\right) \\ &-Q \cdot E_{q \sim P_{n e g}(u)} \log \left(\sigma\left(a_{u}^{T} a_{q}\right)\right) \end{aligned} Lgraph=u∈U∑v∈Nu∪Negu∑−log(σ(auTav))−Q⋅Eq∼Pneg(u)log(σ(auTaq))
其中, N u \mathcal{N}_{u} Nu为节点u的邻居, N e g u \mathcal{N}_{eg_u} Negu为节点u的被标记为负样本的邻居, σ取sigmoid(), P n e g ( u ) ∝ d u 0.75 P_{n e g}(u) \propto d_{u}^{0.75} Pneg(u)∝du0.75 为负样本的采样分布, Q为采样的负样本数量(本文取3).
我们来按照每一项理解一下,
-
− log ( σ ( a u T a v ) ) -\log \left(\sigma\left(a_{u}^{T} a_{v}\right)\right) −log(σ(auTav))
u,v为邻居, 我们希望两个节点的表示是相近的. 若 a u , a v a_u,a_v au,av相近, 则其乘积 a u T a v a^T_ua_v auTav较大, 取sigmoid()后接近1, 取对数后损失小, 符合我们设计Loss的期望.同理, 若 a u , a v a_u,a_v au,av相差较大, 则Loss较大, 给出惩罚
-
− Q ⋅ E q ∼ P n e g ( u ) log ( σ ( a u T a q ) ) -Q \cdot E_{q \sim P_{n e g}(u)} \log \left(\sigma\left(a_{u}^{T} a_{q}\right)\right) −Q⋅Eq∼Pneg(u)log(σ(auTaq))
与上同理, 若邻居中有负样本, 则节点u也可疑, 其节点表示应与负样本节点相近.
注意, 邻居节点v在模型中为random walk path上的点.
-
综上, 我们得到了整个模型的Loss,
L S e m i G N N = α ⋅ L s u p + ( 1 − α ) ⋅ L g r a p h + λ L r e g \mathcal{L}_{S e m i G N N}=\alpha \cdot \mathcal{L}_{s u p}+(1-\alpha) \cdot \mathcal{L}_{g r a p h}+\lambda \mathcal{L}_{r e g} LSemiGNN=α⋅Lsup+(1−α)⋅Lgraph+λLreg
3.6 模型分析
模型主要特点:
- 综合使用异构多维的数据(multiview)
- 可能有较好的解释性(attention)
- 是归纳方法(inductive method), 训练完成后可部署于平台
- 可并行训练的
4. Experiment 实验
4.1 Dataset 数据集
花呗内部数据: 大约4,000,000 有标签用户, 总共100, 000, 000用户.
预处理后, 保留有约90% 的用户, 这些用户的相关view数据确实较少.
预处理后构建了如下4个图(3种view):
- user-relation(用户间关系)
- user-app
- user-nick
- user-address
4.2 实验任务
- user default prediction 用户违约预测
- user attributes prediction 用户特征预测 (本文为用户职业预测)
4.3 实验结果
超越baseline小几个点.
user default prediction:
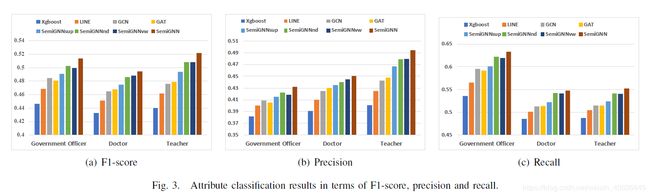
user attributes prediction :
SemiGNNsup为只使用有标签数据的对照组.
结果表明, 在3.6模型分析中提到的优越性, 有助于提升模型性能.
作者后继还对模型参数敏感性, 不同view对性能的重要性进行了简要分析.
-1. One More Thing
个人思考:
-
文章亮点:
- semi-supervised learning 的Loss第一次接触, 略开眼界. 接下来对欺诈检测做进一步了解, 对比各类半监督方案.
- 异构处理. 实质上异构数据是单独处理, 再通过Attention连接来做embedding, 从结果来尚算喜人.
-
一点疑惑:
-
文章中的XGBoost估计没有精调? 在用户职业预测上, 由于有地址信息这一强特征, 个人猜测应该能达到更好的结果. 故模型和业务部署的baseline的差距有多大呢.
-
模型的可解释性仍是薄弱.
文中对模型可解释性的分析, 仅是基于对若干只采用单一view的模型性能做分析, 进而比较attention系数的差异.
-