时间序列分析 - AirPassenger

时间序列分析 - AirPassengers

加载pandas、matplotlib等包，处理时间序列

import pandas as pd
import numpy as np
import matplotlib.pylab as plt

%matplotlib inline
# 解决坐标轴刻度负号乱码
plt.rcParams['axes.unicode_minus'] = False
# 解决中文乱码问题
plt.rcParams['font.sans-serif'] = ['Simhei']

from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 20, 6

import warnings
warnings.filterwarnings("ignore")

data = pd.read_csv('AirPassengers.csv')
data.head()

	Month	#Passengers
0	1949-01	112
1	1949-02	118
2	1949-03	132
3	1949-04	129
4	1949-05	121

data.dtypes

Month          object
#Passengers     int64
dtype: object

data.columns

Index(['Month', '#Passengers'], dtype='object')

Month 是object类型，在时间序列分析中，我们需要现将数据转化为时间序列

第一种方法：将Month以索引读入，转化为时间格式

# 读取数据，pd.read_csv默认生成DataFrame对象，需将其转换成Series对象
df = pd.read_csv('AirPassengers.csv', encoding='utf-8', index_col='Month')
df.head()

	#Passengers
Month
1949-01	112
1949-02	118
1949-03	132
1949-04	129
1949-05	121

df.index = pd.to_datetime(df.index)  # 将字符串索引转换成时间索引
df.head()

	#Passengers
Month
1949-01-01	112
1949-02-01	118
1949-03-01	132
1949-04-01	129
1949-05-01	121

ts = df['#Passengers']  # 生成pd.Series对象
# 查看数据格式
ts.head()

Month
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
Name: #Passengers, dtype: int64

ts.head().index

DatetimeIndex(['1949-01-01', '1949-02-01', '1949-03-01', '1949-04-01',
               '1949-05-01'],
              dtype='datetime64[ns]', name='Month', freq=None)

第二种方法：以时间格式读入Month，并将其设置为索引（推荐）

# pd.read_csv?

dateparse = lambda dates: pd.datetime.strptime(dates, '%Y-%m')
dateparse('1962-01')

datetime.datetime(1962, 1, 1, 0, 0)

df = pd.read_csv('AirPassengers.csv', parse_dates=['Month'], index_col='Month', date_parser=dateparse)
df.head()

	#Passengers
Month
1949-01-01	112
1949-02-01	118
1949-03-01	132
1949-04-01	129
1949-05-01	121

df.shape

(144, 1)

# 检查索引格式
df.index

DatetimeIndex(['1949-01-01', '1949-02-01', '1949-03-01', '1949-04-01',
               '1949-05-01', '1949-06-01', '1949-07-01', '1949-08-01',
               '1949-09-01', '1949-10-01',
               ...
               '1960-03-01', '1960-04-01', '1960-05-01', '1960-06-01',
               '1960-07-01', '1960-08-01', '1960-09-01', '1960-10-01',
               '1960-11-01', '1960-12-01'],
              dtype='datetime64[ns]', name='Month', length=144, freq=None)

# convert to time series:
ts = df['#Passengers']
ts.head(10)

Month
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
1949-06-01    135
1949-07-01    148
1949-08-01    148
1949-09-01    136
1949-10-01    119
Name: #Passengers, dtype: int64

检索时间序列

检索特定时间的序列值

# 1. 检索特定时间的序列值
ts['1949-01-01']

112

# 2. 导入datetime的datetime模块，生成索引检索特定时间的序列值
from datetime import datetime
ts[datetime(1949,1,1)]

112

获取一定时间区间的序列值

# 1. 切片，指定区间
ts['1949-01-01':'1949-05-01']

Month
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
Name: #Passengers, dtype: int64

# 2. 切片，从开始到指定时间点
ts[:'1949-05-01']

Month
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
Name: #Passengers, dtype: int64

Note: ends included here

# 所有1949年的数据
ts['1949']

Month
1949-01-01    112
1949-02-01    118
1949-03-01    132
1949-04-01    129
1949-05-01    121
1949-06-01    135
1949-07-01    148
1949-08-01    148
1949-09-01    136
1949-10-01    119
1949-11-01    104
1949-12-01    118
Name: #Passengers, dtype: int64

min(ts.index), max(ts.index)

(Timestamp('1949-01-01 00:00:00'), Timestamp('1960-12-01 00:00:00'))

平稳性检验

绘制时序图

plt.plot(ts);

[外链图片转存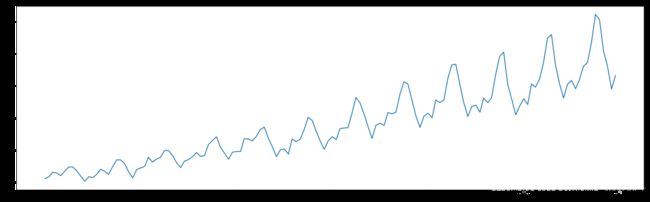(img-y6tQm2EE-1562729474892)(output_30_0.png)]

平稳性检验

# 移动平均
# pd.rolling_mean?

from statsmodels.tsa.stattools import adfuller

def test_stationarity(timeseries):
    # Determing rolling statistics
    rolmean = timeseries.rolling(window=12, center=False).mean()
    rolstd =  timeseries.rolling(window=12, center=False).std()
    
    # Plot rolling statistics:
    orig = plt.plot(timeseries, color='blue', label='Original')
    mean = plt.plot(rolmean, color='red', label='Rolling Mean')
    std = plt.plot(rolstd, color='black', label = 'Rolling Std')
    plt.legend(loc='best')
    plt.title('Rolling Mean & Standard Deviation')
    plt.show(block=False)
    
    # Perform Dickey-Fuller test:
    print('Results of Dickey-Fuller Test:')
    dftest = adfuller(timeseries, autolag='AIC')
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
    for key,value in dftest[4].items():
        dfoutput['Critical Value ({})'.format(key)] = value
    print(dfoutput)

test_stationarity(ts)

[外链图片转存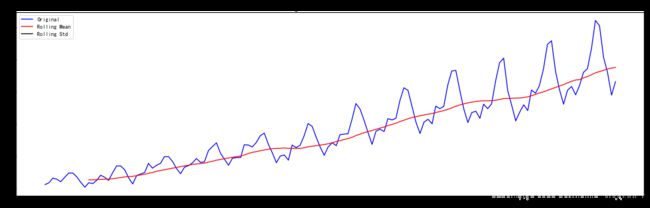(img-FSxx9adZ-1562729474893)(output_34_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                   0.815369
p-value                          0.991880
#Lags Used                      13.000000
Number of Observations Used    130.000000
Critical Value (1%)             -3.481682
Critical Value (5%)             -2.884042
Critical Value (10%)            -2.578770
dtype: float64

p = 0.991880 > 0.05 序列非平稳, 同时也可以注意到均值和方差很不稳定

# acorr_ljungbox?

from statsmodels.stats.diagnostic import acorr_ljungbox

# 白噪声检验：Ljung-Box test
def randomness(ts, lags=10):
    rdtest = acorr_ljungbox(ts,lags=lags)
    # 对上述函数求得的值进行语义描述
    rddata = np.c_[range(1,lags+1),rdtest[1:][0]]
    rdoutput = pd.DataFrame(rddata,columns=['lags','p-value'])
    return rdoutput.set_index('lags')

randomness(ts)

	p-value
lags
1.0	1.393231e-30
2.0	4.556318e-54
3.0	5.751088e-74
4.0	2.817731e-91
5.0	7.360195e-107
6.0	4.264008e-121
7.0	1.305463e-134
8.0	6.496271e-148
9.0	5.249370e-162
10.0	1.100789e-177

p = 1.3932314e-30 < 0.05，序列为非白噪声序列

平稳性处理 - 估计和消除趋势

消除趋势的第一个诀窍是对数变换。因为，能清楚地看到我们的数据呈现一个显著的上升趋势。因此，我们可以应用log变换。当然还有其他的变换方式，如：平方根，立方根等等。

[外链图片转存失败(img-lWuJFawA-1562729474893)(log 函数曲线.jpg)]

对数变换(log transform)

ts_log = np.log(ts)

# Plot original ts and log(ts):
plt.subplot(211)
plt.title('Original')
plt.plot(ts,label='Original ts')
plt.legend(loc='best')
plt.subplot(212)
plt.title('Log')
plt.plot(ts_log, label='Log(ts)')
plt.legend(loc='best')
plt.tight_layout()

[外链图片转存(img-zYLSvexy-1562729474894)(output_44_0.png)]

平滑法/移动平均法(Moving average)

moving_avg = ts_log.rolling(window=12,center=False).mean()  # 窗口为12
plt.plot(ts_log, label='Original')
plt.plot(moving_avg, color='red', label='Moving average')
plt.title('Moving average(12)')
plt.legend(loc='best');

[外链图片转存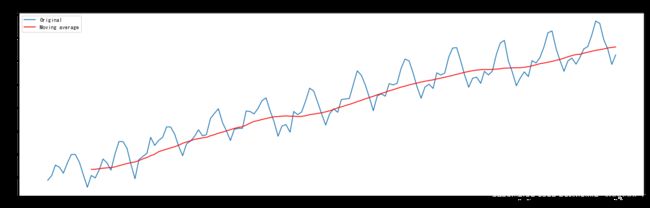(img-gWMOPmSo-1562729474894)(output_46_0.png)]

# 移除移动平均值
ts_log_moving_avg_diff = ts_log - moving_avg
ts_log_moving_avg_diff.head(24)

Month
1949-01-01         NaN
1949-02-01         NaN
1949-03-01         NaN
1949-04-01         NaN
1949-05-01         NaN
1949-06-01         NaN
1949-07-01         NaN
1949-08-01         NaN
1949-09-01         NaN
1949-10-01         NaN
1949-11-01         NaN
1949-12-01   -0.065494
1950-01-01   -0.093449
1950-02-01   -0.007566
1950-03-01    0.099416
1950-04-01    0.052142
1950-05-01   -0.027529
1950-06-01    0.139881
1950-07-01    0.260184
1950-08-01    0.248635
1950-09-01    0.162937
1950-10-01   -0.018578
1950-11-01   -0.180379
1950-12-01    0.010818
Name: #Passengers, dtype: float64

ts_log_moving_avg_diff.dropna(inplace=True)
ts_log_moving_avg_diff.head()

Month
1949-12-01   -0.065494
1950-01-01   -0.093449
1950-02-01   -0.007566
1950-03-01    0.099416
1950-04-01    0.052142
Name: #Passengers, dtype: float64

test_stationarity(ts_log_moving_avg_diff)

[外链图片转存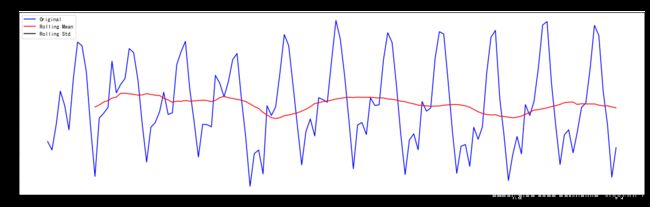(img-yPo4GPsI-1562729474895)(output_49_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                  -3.162908
p-value                          0.022235
#Lags Used                      13.000000
Number of Observations Used    119.000000
Critical Value (1%)             -3.486535
Critical Value (5%)             -2.886151
Critical Value (10%)            -2.579896
dtype: float64

p = 0.022235 < 0.05 我们可以说在95%的置信度下该序列平稳，均值和方差比平滑法相对稳定

然而，这种特殊方法的一个缺点是，必须严格定义时间周期。在这种情况下，我们可以取年平均，但在复杂的情况下，比如预测股票价格，很难通过这种方法达到平稳。所以我们取一个“加权移动平均”(weighted moving average)，该方法中最近的时序值被赋予更高的权重。有很多方法可以分配权重。最常用的是指数加权移动平均，权重被分配到所有之前的值。

指数加权平滑法(exponentially weighted moving average)

# ts_log.ewm?

expwighted_avg = ts_log.ewm(min_periods=0, ignore_na=False, halflife=12, adjust=True).mean()
plt.plot(ts_log, label='Original')
plt.plot(moving_avg, color='red', label='Moving average')
plt.plot(expwighted_avg, color='green', label='Weighted Moving average')
# expwighted_avg.plot(style='k--')
plt.title('Moving Average(12) & weighted Moving Average(12)')
plt.legend(loc='best');

[外链图片转存(img-jej2P1qZ-1562729474895)(output_53_0.png)]

# 移除指数加权移动平均值
ts_log_ewma_diff = ts_log - expwighted_avg
test_stationarity(ts_log_ewma_diff)

[外链图片转存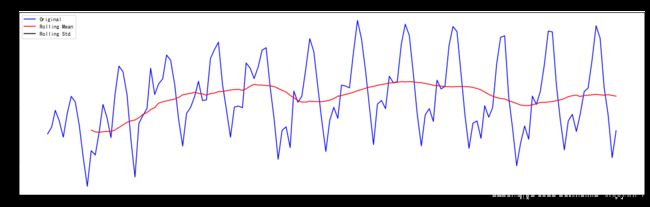(img-spwk5QIJ-1562729474895)(output_54_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                  -3.601262
p-value                          0.005737
#Lags Used                      13.000000
Number of Observations Used    130.000000
Critical Value (1%)             -3.481682
Critical Value (5%)             -2.884042
Critical Value (10%)            -2.578770
dtype: float64

p = 0.005737 现在可以说在99%的置信度下该序列平稳，均值和方差更加稳定

并且注意这里没有产生缺失值

消除趋势和季节因素

前面提到的方法不是对所有的问题都能做到很好的解决，尤其是在有比较明显的季节性因素存在的时候。下面我们会讲到两个常用而且有效地方法来消除趋势项和季节性因素：

• 差分：以一定的时间间隔做差分
• 分解：对趋势和季节性进行建模，并将它们从模型中移除

差分

# 一阶差分
ts_log_diff = ts_log - ts_log.shift()
plt.plot(ts_log_diff);

[外链图片转存(img-OJI8GEMZ-1562729474896)(output_58_0.png)]

ts_log_diff.dropna(inplace=True)
test_stationarity(ts_log_diff)

[外链图片转存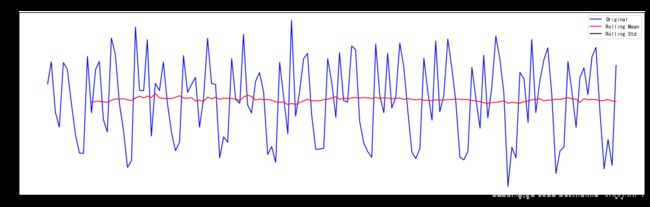(img-7tziORx9-1562729474896)(output_59_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                  -2.717131
p-value                          0.071121
#Lags Used                      14.000000
Number of Observations Used    128.000000
Critical Value (1%)             -3.482501
Critical Value (5%)             -2.884398
Critical Value (10%)            -2.578960
dtype: float64

p = 0.071121 可以说在90%的置信度下该序列平稳，均值和方差很稳定

分解

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)

trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid

plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()

[外链图片转存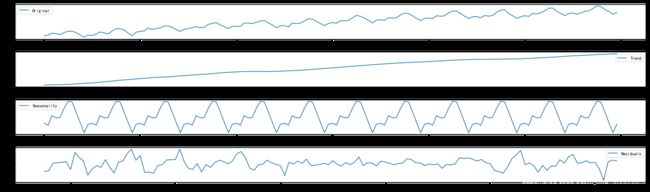(img-4GU2jwWs-1562729474896)(output_62_0.png)]

# 检验残差的平稳性
ts_log_decompose = residual
ts_log_decompose.dropna(inplace=True)
test_stationarity(ts_log_decompose)

[外链图片转存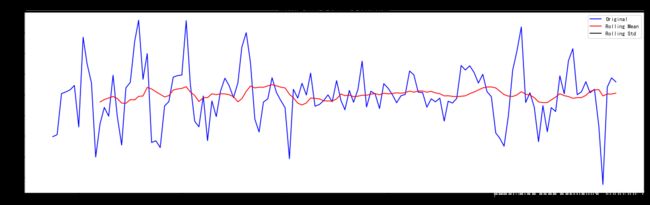(img-RBRWLtFc-1562729474896)(output_63_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                -6.332387e+00
p-value                        2.885059e-08
#Lags Used                     9.000000e+00
Number of Observations Used    1.220000e+02
Critical Value (1%)           -3.485122e+00
Critical Value (5%)           -2.885538e+00
Critical Value (10%)          -2.579569e+00
dtype: float64

模型拟合

ARMA

from statsmodels.tsa.arima_model import ARIMA

ACF & PACF Plots

# ACF and PACF plots:
from statsmodels.tsa.stattools import acf, pacf  

# ts_log_diff， log变换后做一阶差分后的时序
lag_acf = acf(ts_log_diff, nlags=30)
lag_pacf = pacf(ts_log_diff, nlags=30, method='ols')

# Plot ACF:
plt.subplot(121)    
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Autocorrelation Function')

# Plot PACF:
plt.subplot(122)
plt.plot(lag_pacf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_log_diff)),linestyle='--',color='gray')
plt.title('Partial Autocorrelation Function')
plt.tight_layout()

[外链图片转存(img-v5iIBEYw-1562729474897)(output_68_0.png)]

可以看到ACF和PACF分别在2阶的时候第一次落到置信区间内

# 其实，statsmodels提供了更加方便的话ACF，PACF的函数
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

# 自相关和偏相关图，默认阶数为31阶
def draw_acf_pacf(ts, lags=31):
    f = plt.figure(facecolor='white',figsize=(20,4))
    ax1 = f.add_subplot(121)
    plot_acf(ts, lags=31, ax=ax1)
    ax2 = f.add_subplot(122)
    plot_pacf(ts, lags=31, ax=ax2)
    plt.show()

draw_acf_pacf(ts)

[外链图片转存(img-0IlJORmw-1562729474897)(output_72_0.png)]

draw_acf_pacf(ts_log_diff)

[外链图片转存(img-zyzeAv4N-1562729474897)(output_73_0.png)]

AR Model:

model = ARIMA(ts_log, order=(2, 1, 0))
results_AR = model.fit(disp=-1)
plt.plot(ts_log_diff)
plt.plot(results_AR.fittedvalues, color='red')
plt.title('RSS: {:.4f}'.format(sum((results_AR.fittedvalues-ts_log_diff)**2)));

[外链图片转存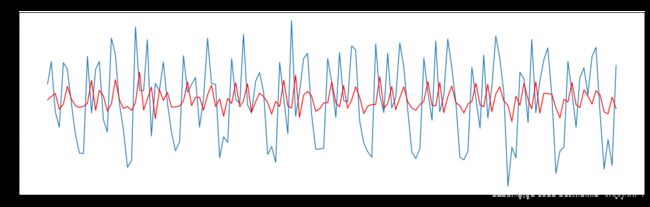(img-5qz998lw-1562729474898)(output_75_0.png)]

MA Model

model = ARIMA(ts_log, order=(0, 1, 2))  
results_MA = model.fit(disp=-1)  
plt.plot(ts_log_diff)
plt.plot(results_MA.fittedvalues, color='red')
plt.title('RSS: {:.4f}'.format(sum((results_MA.fittedvalues-ts_log_diff)**2)));

[外链图片转存(img-VHpE4QzO-1562729474898)(output_77_0.png)]

ARIMA Model:

model = ARIMA(ts_log, order=(2, 1, 2))  
results_ARIMA = model.fit(disp=-1)
print(results_ARIMA.summary())

                             ARIMA Model Results                              
==============================================================================
Dep. Variable:          D.#Passengers   No. Observations:                  143
Model:                 ARIMA(2, 1, 2)   Log Likelihood                 149.640
Method:                       css-mle   S.D. of innovations              0.084
Date:                Mon, 03 Sep 2018   AIC                           -287.281
Time:                        16:39:28   BIC                           -269.504
Sample:                    02-01-1949   HQIC                          -280.057
                         - 12-01-1960                                         
=======================================================================================
                          coef    std err          z      P>|z|      [0.025      0.975]
---------------------------------------------------------------------------------------
const                   0.0096      0.003      3.697      0.000       0.005       0.015
ar.L1.D.#Passengers     1.6293      0.039     41.868      0.000       1.553       1.706
ar.L2.D.#Passengers    -0.8946      0.039    -23.127      0.000      -0.970      -0.819
ma.L1.D.#Passengers    -1.8270      0.036    -51.303      0.000      -1.897      -1.757
ma.L2.D.#Passengers     0.9245      0.036     25.568      0.000       0.854       0.995
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            0.9106           -0.5372j            1.0573           -0.0848
AR.2            0.9106           +0.5372j            1.0573            0.0848
MA.1            0.9881           -0.3245j            1.0400           -0.0505
MA.2            0.9881           +0.3245j            1.0400            0.0505
-----------------------------------------------------------------------------

plt.plot(ts_log_diff)
plt.plot(results_ARIMA.fittedvalues, color='red')
plt.title('RSS: {:.4f}'.format(sum((results_ARIMA.fittedvalues-ts_log_diff)**2)));

[外链图片转存(img-ak6oboSI-1562729474898)(output_80_0.png)]

将预测值转化为变换前的值:

predictions_ARIMA_diff = pd.Series(results_ARIMA.fittedvalues, copy=True)
predictions_ARIMA_diff.head()

Month
1949-02-01    0.009580
1949-03-01    0.017491
1949-04-01    0.027670
1949-05-01   -0.004521
1949-06-01   -0.023889
dtype: float64

predictions_ARIMA_diff.tail()

Month
1960-08-01   -0.041176
1960-09-01   -0.092350
1960-10-01   -0.094013
1960-11-01   -0.069924
1960-12-01   -0.008127
dtype: float64

# 消除一阶差分的影响
predictions_ARIMA_diff_cumsum = predictions_ARIMA_diff.cumsum()
predictions_ARIMA_diff_cumsum.head()

Month
1949-02-01    0.009580
1949-03-01    0.027071
1949-04-01    0.054742
1949-05-01    0.050221
1949-06-01    0.026331
dtype: float64

ts_log.iloc[0]

4.718498871295094

# 将1949-01-01的值添加回来，并以此为基数，变换回差分前
predictions_ARIMA_log = pd.Series(ts_log.iloc[0], index=ts_log.index)
predictions_ARIMA_log = predictions_ARIMA_log.add(predictions_ARIMA_diff_cumsum, fill_value=0)
predictions_ARIMA_log.head()

Month
1949-01-01    4.718499
1949-02-01    4.728079
1949-03-01    4.745570
1949-04-01    4.773241
1949-05-01    4.768720
dtype: float64

plt.plot(ts_log)
plt.plot(predictions_ARIMA_log);

[外链图片转存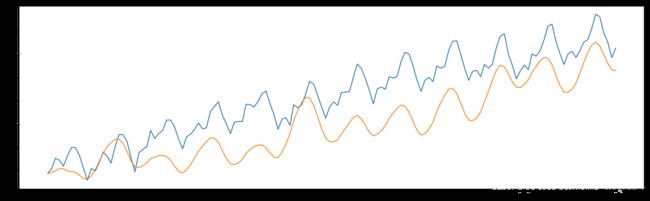(img-U5LE6Pad-1562729474899)(output_87_0.png)]

predictions_ARIMA = np.exp(predictions_ARIMA_log)
predictions_ARIMA.head()

Month
1949-01-01    112.000000
1949-02-01    113.078122
1949-03-01    115.073413
1949-04-01    118.301983
1949-05-01    117.768360
dtype: float64

plt.plot(ts)
plt.plot(predictions_ARIMA)
plt.title('RMSE: {:.4f}'.format(np.sqrt(sum((predictions_ARIMA-ts)**2)/len(ts))));

[外链图片转存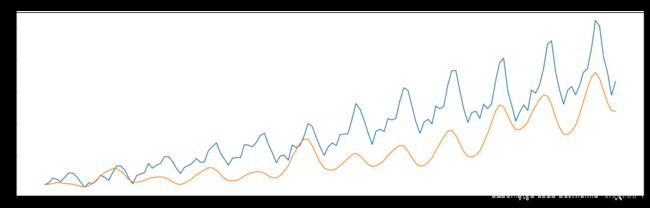(img-mVcPVaXi-1562729474899)(output_89_0.png)]

SARMAX

import statsmodels.api as sm

draw_acf_pacf(ts)

[外链图片转存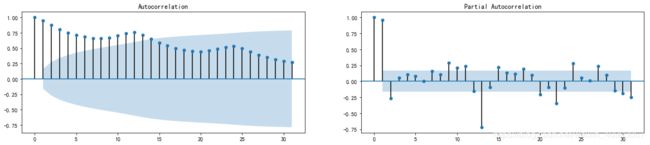(img-EFwoHjxx-1562729474899)(output_92_0.png)]

# Fit the model
mod = sm.tsa.statespace.SARIMAX(ts_log, order=(1,1,1), seasonal_order=(1,0,0,12), simple_differencing=True)
res = mod.fit(disp=False)
print(res.summary())

                                 Statespace Model Results                                 
==========================================================================================
Dep. Variable:                      D.#Passengers   No. Observations:                  143
Model:             SARIMAX(1, 0, 1)x(1, 0, 0, 12)   Log Likelihood                 237.983
Date:                            Mon, 03 Sep 2018   AIC                           -467.965
Time:                                    16:39:36   BIC                           -456.114
Sample:                                02-01-1949   HQIC                          -463.149
                                     - 12-01-1960                                         
Covariance Type:                              opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
ar.L1         -0.4712      0.285     -1.652      0.099      -1.030       0.088
ma.L1          0.2038      0.312      0.653      0.514      -0.408       0.815
ar.S.L12       0.9275      0.028     33.439      0.000       0.873       0.982
sigma2         0.0018      0.000      9.367      0.000       0.001       0.002
===================================================================================
Ljung-Box (Q):                       52.52   Jarque-Bera (JB):                 2.94
Prob(Q):                              0.09   Prob(JB):                         0.23
Heteroskedasticity (H):               0.50   Skew:                             0.22
Prob(H) (two-sided):                  0.02   Kurtosis:                         3.54
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

# In-sample one-step-ahead predictions, and out-of-sample forecasts
nforecast = 12
predict = res.get_prediction(end=mod.nobs + nforecast)

# 消除一阶差分的影响
pred_log = pd.Series(ts_log.iloc[0], index=ts_log[[0]].index)
pred_log = pred_log.add(predict.predicted_mean, fill_value=0).cumsum()
# 对数还原
pred_ARIMA = np.exp(pred_log)

# Graph
fig, ax = plt.subplots(figsize=(12,6))
ax.xaxis.grid()
ax.plot(ts, 'k.')
# Plot
ax.plot(pred_ARIMA[:-nforecast-1], 'b')
ax.plot(pred_ARIMA[-nforecast-1:], 'k--', linestyle='--', linewidth=2)
ax.set(title='RMSE: {:.4f}'.format(np.sqrt(sum((pred_ARIMA[:-nforecast-1]-ts)**2)/len(ts))));

[外链图片转存(img-5VgKJk1E-1562729474899)(output_96_0.png)]

进一步调优

# log变换，平滑，一阶差分
ts_log = np.log(ts)
rol_mean = ts_log.rolling(window=12).mean()
rol_mean.dropna(inplace=True)
ts_diff_1 = rol_mean.diff(1)
ts_diff_1.dropna(inplace=True)
test_stationarity(ts_diff_1)

[外链图片转存(img-NF1IHiw2-1562729474900)(output_98_0.png)]

Results of Dickey-Fuller Test:
Test Statistic                  -2.709577
p-value                          0.072396
#Lags Used                      12.000000
Number of Observations Used    119.000000
Critical Value (1%)             -3.486535
Critical Value (5%)             -2.886151
Critical Value (10%)            -2.579896
dtype: float64

# 二阶差分
ts_diff_2 = ts_diff_1.diff(1)
ts_diff_2.dropna(inplace=True)

from statsmodels.tsa.arima_model import ARMA

# 拟合模型
model = ARMA(ts_diff_2, order=(1, 1))
result_arma = model.fit(disp=-1, method='css')

# 预测值
result_arma.fittedvalues.head()

Month
1950-03-01    0.000536
1950-04-01    0.000283
1950-05-01    0.000801
1950-06-01    0.000844
1950-07-01   -0.001620
dtype: float64

print(result_arma.summary())

                              ARMA Model Results                              
==============================================================================
Dep. Variable:            #Passengers   No. Observations:                  131
Model:                     ARMA(1, 1)   Log Likelihood                 548.413
Method:                           css   S.D. of innovations              0.004
Date:                Mon, 03 Sep 2018   AIC                          -1088.826
Time:                        16:39:41   BIC                          -1077.356
Sample:                    03-01-1950   HQIC                         -1084.165
                         - 12-01-1960                                         
=====================================================================================
                        coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------------
const              4.899e-06      0.000      0.028      0.977      -0.000       0.000
ar.L1.#Passengers     0.1630      0.259      0.630      0.530      -0.345       0.671
ma.L1.#Passengers    -0.5404      0.229     -2.355      0.020      -0.990      -0.091
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            6.1335           +0.0000j            6.1335            0.0000
MA.1            1.8504           +0.0000j            1.8504            0.0000
-----------------------------------------------------------------------------

# AIC，BIC
result_arma.aic, result_arma.bic

(-1088.8260693802756, -1077.3559315784532)

# AR，MA模型参数估计
result_arma.arparams, result_arma.maparams

(array([0.16304032]), array([-0.54041254]))

# 预测值
predict_ts = result_arma.predict()
predict_ts.head(), predict_ts.tail()

(1950-03-01    0.000536
 1950-04-01    0.000283
 1950-05-01    0.000801
 1950-06-01    0.000844
 1950-07-01   -0.001620
 Freq: MS, dtype: float64, 1960-08-01   -0.000151
 1960-09-01    0.001367
 1960-10-01    0.000365
 1960-11-01   -0.000800
 1960-12-01    0.001147
 Freq: MS, dtype: float64)

样本外预测

forecast方法(Out-of-sample forecasts):

arma_model.forecast(steps=1, exog=None, alpha=0.05)

参数：

• step:预测步长
• exog:外生变量（armax）
• alpha:预测的置信水平

返回：

• forecast:预测值，数组
• stderr:标准差，数组
• conf_int:预测值的执行区间，二维数组

# result_arma.forecast?

result_arma.forecast(1) # 1步预测

(array([0.00093721]), array([0.00356176]), array([[-0.00604371,  0.00791813]]))

result_arma.forecast(1)[0] # 1步预测

array([0.00093721])

result_arma.forecast(10)[0] # 10步预测

array([9.37208646e-04, 1.56903477e-04, 2.96822730e-05, 8.94008713e-06,
       5.55827452e-06, 5.00690271e-06, 4.91700687e-06, 4.90235022e-06,
       4.89996060e-06, 4.89957099e-06])

predict方法

可以用来预测任意的样本内和样本外的时间步长。

arma_model.predict(start=None, end=None, exog=None, dynamic=False)

参数：

• start:预测开始时间(可以是时间格式也可以是可以转化为时间格式的字符串)或训练数据的索引,1阶差分从1开始，以此类推
• end:预测开始时间(可以是时间格式也可以是可以转化为时间格式的字符串)或训练数据的索引,1阶差分从1开始，以此类推
• exog:外生变量（armax）
• dynamic:False，样本内滞后值会被用作预测，True，样本内预测值被用来代替滞后值

返回：

• predict : 预测值，数组

# result_arma.predict?

from pandas import datetime

start_index = datetime(1961, 1, 1)
end_index = datetime(1961, 12, 1)
pred = result_arma.predict(start=start_index, end=end_index)
pred.head(), pred.tail()

(1961-01-01    0.000937
 1961-02-01    0.000157
 1961-03-01    0.000030
 1961-04-01    0.000009
 1961-05-01    0.000006
 Freq: MS, dtype: float64, 1961-08-01    0.000005
 1961-09-01    0.000005
 1961-10-01    0.000005
 1961-11-01    0.000005
 1961-12-01    0.000005
 Freq: MS, dtype: float64)

# 变换过后的实际值和预测值
plt.figure(figsize=(8,5))
result_arma.plot_predict();

[外链图片转存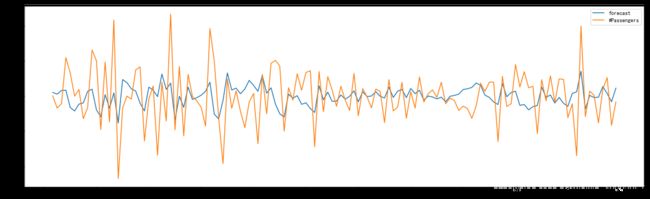(img-8UGOYSwh-1562729474900)(output_115_1.png)]

# 还原

# 一阶差分还原
diff_shift_ts = ts_diff_1.shift(1)
diff_recover_1 = predict_ts.add(diff_shift_ts)
# 再次一阶差分还原
rol_shift_ts = rol_mean.shift(1)
diff_recover = diff_recover_1.add(rol_shift_ts)
# 移动平均还原
rol_sum = ts_log.rolling(window=11).sum()
rol_recover = diff_recover * 12 - rol_sum.shift(1)
# 对数还原
log_recover = np.exp(rol_recover)
log_recover.head()

1949-01-01   NaN
1949-02-01   NaN
1949-03-01   NaN
1949-04-01   NaN
1949-05-01   NaN
dtype: float64

log_recover.tail(15)

1959-10-01    406.530462
1959-11-01    350.627418
1959-12-01    388.688005
1960-01-01    425.142956
1960-02-01    397.935468
1960-03-01    467.625349
1960-04-01    426.505252
1960-05-01    478.137753
1960-06-01    531.118845
1960-07-01    619.599772
1960-08-01    633.334409
1960-09-01    510.229116
1960-10-01    448.515536
1960-11-01    406.112839
1960-12-01    442.372193
dtype: float64

log_recover.dropna(inplace=True)
log_recover.head(), log_recover.tail()

(1950-03-01    141.859017
 1950-04-01    138.263428
 1950-05-01    127.851420
 1950-06-01    140.882557
 1950-07-01    160.203376
 dtype: float64, 1960-08-01    633.334409
 1960-09-01    510.229116
 1960-10-01    448.515536
 1960-11-01    406.112839
 1960-12-01    442.372193
 dtype: float64)

ts1 = ts[log_recover.index]  # 过滤没有预测的记录

plt.figure(facecolor='white')
log_recover.plot(color='green', label='Predict')
ts.plot(color='grey', label='Original')
plt.legend(loc='best')
plt.title('RMSE: {:.4f}'.format(np.sqrt(sum((log_recover-ts1)**2)/ts1.size)));

[外链图片转存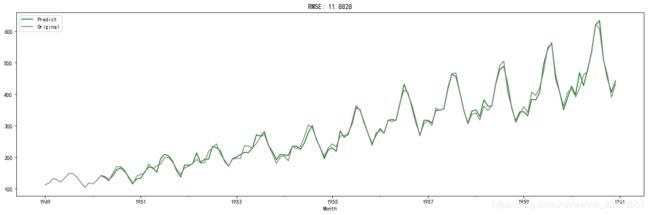(img-qJfRRaNQ-1562729474900)(output_119_0.png)]

# 差分操作
def diff_ts(ts, d):
    global shift_ts_list
    #  动态预测第二日的值时所需要的差分序列
    global last_data_shift_list
    shift_ts_list = []
    last_data_shift_list = []
    tmp_ts = ts
    for i in d:
        last_data_shift_list.append(tmp_ts[-i])
        print(last_data_shift_list)
        shift_ts = tmp_ts.shift(i)
        shift_ts_list.append(shift_ts)
        tmp_ts = tmp_ts - shift_ts
    tmp_ts.dropna(inplace=True)
    return tmp_ts

# 还原操作
def predict_diff_recover(predict_value, d):
    if isinstance(predict_value, float):
        tmp_data = predict_value
        for i in range(len(d)):
            tmp_data = tmp_data + last_data_shift_list[-i-1]
    elif isinstance(predict_value, np.ndarray):
        tmp_data = predict_value[0]
        for i in range(len(d)):
            tmp_data = tmp_data + last_data_shift_list[-i-1]
    else:
        tmp_data = predict_value
        for i in range(len(d)):
            try:
                tmp_data = tmp_data.add(shift_ts_list[-i-1])
            except:
                raise ValueError('What you input is not pd.Series type!')
        tmp_data.dropna(inplace=True)
    return tmp_data

# 模型调优
def proper_model(data_ts, maxLag):
    import sys
    init_bic = sys.maxsize
    init_p = 0
    init_q = 0
    init_properModel = None
    for p in np.arange(maxLag):
        for q in np.arange(maxLag):
            model = ARMA(data_ts, order=(p, q))
            try:
                results_ARMA = model.fit(disp=-1, method='css')
            except:
                continue
            bic = results_ARMA.bic
            if bic < init_bic:
                init_p = p
                init_q = q
                init_properModel = results_ARMA
                init_bic = bic
    print("最优模型的BIC为：{}；p为：{}；q为：{}".format(init_bic, init_p, init_q))
    return init_bic, init_p, init_q, init_properModel

diffed_ts = diff_ts(ts_log, d=[12, 1])
bic, p, q, properModel = proper_model(diffed_ts, 3)
predict_ts = properModel.predict()
diff_recover_ts = predict_diff_recover(predict_ts, d=[12, 1])
log_recover = np.exp(diff_recover_ts)

[6.0330862217988015]
[6.0330862217988015, 0.06453852113757197]
最优模型的BIC为：-439.3965513369529；p为：0；q为：1

ts1 = ts[log_recover.index]  # 过滤没有预测的记录

plt.figure(facecolor='white')
log_recover.plot(color='green', label='Predict')
ts1.plot(color='grey', label='Original')
plt.legend(loc='best')
plt.title('RMSE: {:.4f}'.format(np.sqrt(sum((log_recover-ts1)**2)/ts1.size)));

[外链图片转存(img-yMDA3YDr-1562729474901)(output_122_0.png)]

实时预测

from dateutil.relativedelta import relativedelta

def _add_new_data(ts, dat, type='day'):
    if type == 'day':
        new_index = ts.index[-1] + relativedelta(days=1)
    elif type == 'month':
        new_index = ts.index[-1] + relativedelta(months=1)
    ts[new_index] = dat

def add_today_data(model, ts,  data, d, type='day'):
    _add_new_data(ts, data, type)  # 为原始序列添加数据
    # 为滞后序列添加新值
    d_ts = diff_ts(ts, d)
#     model.add_today_data(d_ts[-1], type)
    return d_ts

def forecast_next(model,dta):
    if model == None:
        raise ValueError('No model fitted before')
    fc = model.forecast(1)[0]  # 1步预测
    return predict_diff_recover(fc, [12, 1])

ts_train = ts_log[:'1956-12']
ts_test = ts_log['1957-1':]

diffed_ts = diff_ts(ts_train, [12, 1])
forecast_list = []

for i, dta in enumerate(ts_test):
    if i % 7 == 0:
        bic, p, q, properModel = proper_model(diffed_ts, 3)
    forecast_data = forecast_next(properModel, dta)
    forecast_list.append(forecast_data)
    diffed_ts = add_today_data(properModel, ts_train, dta, [12, 1], type='month')

[5.648974238161206]
[5.648974238161206, 0.0959639882617438]
最优模型的BIC为：-258.1964284797439；p为：0；q为：1
[5.6240175061873385]
[5.6240175061873385, 0.10359840066442683]
[5.75890177387728]
[5.75890177387728, 0.08309275856153686]
[5.746203190540153]
[5.746203190540153, 0.11602895697475013]
[5.762051382780177]
[5.762051382780177, 0.10599928923432156]
[5.924255797414532]
[5.924255797414532, 0.11006640669523904]
[6.023447592961033]
[6.023447592961033, 0.12074951662147981]
[6.003887067106539]
[6.003887067106539, 0.11858981262632273]
最优模型的BIC为：-287.52098131248624；p为：0；q为：1
[5.872117789475416]
[5.872117789475416, 0.14244219056235874]
[5.723585101952381]
[5.723585101952381, 0.1292970884857345]
[5.602118820879701]
[5.602118820879701, 0.1257396779944786]
[5.723585101952381]
[5.723585101952381, 0.11819295572771082]
[5.752572638825633]
[5.752572638825633, 0.09352605801082348]
[5.707110264748875]
[5.707110264748875, 0.07637297878457439]
[5.87493073085203]
[5.87493073085203, 0.05494111803130153]
最优模型的BIC为：-316.12436720936176；p为：0；q为：1
[5.8522024797744745]
[5.8522024797744745, 0.016713480973741035]
[5.872117789475416]
[5.872117789475416, 0.0]
[6.045005314036012]
[6.045005314036012, 0.022285044789434494]
[6.142037405587356]
[6.142037405587356, 0.03034071705267216]
[6.1463292576688975]
[6.1463292576688975, 0.05440672220716447]
[6.0014148779611505]
[6.0014148779611505, 0.0782291716064627]
[5.849324779946859]
[5.849324779946859, 0.0]
最优模型的BIC为：-341.4698836569178；p为：0；q为：1
[5.720311776607412]
[5.720311776607412, 0.03399760854141931]
[5.817111159963204]
[5.817111159963204, 0.016260520871780315]
[5.8289456176102075]
[5.8289456176102075, 0.002971770389157413]
[5.762051382780177]
[5.762051382780177, 0.05715841383994835]
[5.8916442118257715]
[5.8916442118257715, 0.07275935428242786]
[5.8522024797744745]
[5.8522024797744745, 0.11470894777596108]
[5.8944028342648505]
[5.8944028342648505, 0.1292117314800061]
最优模型的BIC为：-368.1436197652257；p为：0；q为：1
[6.075346031088684]
[6.075346031088684, 0.1458518770125634]
[6.19644412779452]
[6.19644412779452, 0.0816329544968708]
[6.22455842927536]
[6.22455842927536, 0.1098311591534955]
[6.0014148779611505]
[6.0014148779611505, 0.10159104387973894]
[5.883322388488279]
[5.883322388488279, 0.13631217612508362]
[5.736572297479192]
[5.736572297479192, 0.12549079695431598]
[5.820082930352362]
[5.820082930352362, 0.1550719143465793]
最优模型的BIC为：-396.06450849453194；p为：0；q为：1
[5.886104031450156]
[5.886104031450156, 0.18380413675417717]
[5.834810737062605]
[5.834810737062605, 0.14698219034864568]
[6.0063531596017325]
[6.0063531596017325, 0.13389682292276106]
[5.981414211254481]
[5.981414211254481, 0.031517760320404875]
[6.040254711277414]
[6.040254711277414, 0.151983831742168]
[6.156978985585555]
[6.156978985585555, 0.11672427430814114]
[6.306275286948016]
[6.306275286948016, 0.12528776131045127]
最优模型的BIC为：-415.59182822959184；p为：0；q为：1
[6.326149473155099]
[6.326149473155099, 0.12666480579116346]
[6.137727054086234]
[6.137727054086234, 0.08073051291421507]
[6.008813185442595]
[6.008813185442595, 0.0927543934922479]
[5.8916442118257715]
[5.8916442118257715, 0.12458485755405402]
[6.003887067106539]
[6.003887067106539, 0.07450252729792073]
[6.0330862217988015]
[6.0330862217988015, 0.06453852113757197]

predict_ts = pd.Series(data=forecast_list, index=ts['1957-1':].index)
log_recover = np.exp(predict_ts)
# original_ts = ts['1957-1':]

ts1 = ts[log_recover.index]  # 过滤没有预测的记录
plt.figure(facecolor='white')
log_recover.plot(color='green', label='Predict')
ts.plot(color='grey', label='Original')
plt.legend(loc='best')
plt.title('RMSE: {:.4f}'.format(np.sqrt(sum((log_recover-ts1)**2)/ts1.size)));

[外链图片转存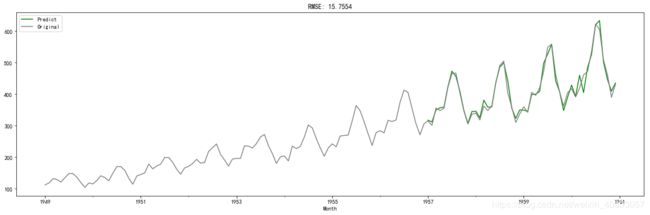(img-PoHYPx3v-1562729474901)(output_127_0.png)]

plt.figure(facecolor='white')
log_recover.plot(color='green', label='Predict')
ts['1957-1':].plot(color='grey', label='Original')
plt.legend(loc='best')
plt.title('RMSE: {:.4f}'.format(np.sqrt(sum((log_recover-ts1)**2)/ts1.size)));