机器学习笔记006 | 更加准确的拟合，更加快速地收敛

1 更加准确的拟合

假如我们有一些房价的数据，其落点是这样的：

房价

对于这样的一些价格和面积数据，如果通过线性回归的方式，不管预测的直线怎么放，你都会发现不能很好的拟合已有的数据。

这时候，为了更好地拟合数据，我们可以使用多项式回归（polynomial regression）。

例如二次多项式：h_θ(x) = θ₀ + θ₁x + θ₂x²

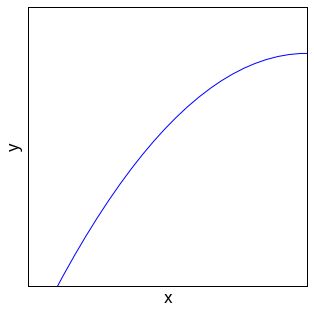
其曲线可能是这样的：

例如三次多项式：h_θ(x) = θ₀ + θ₁x + θ₂x² + θ₃x³

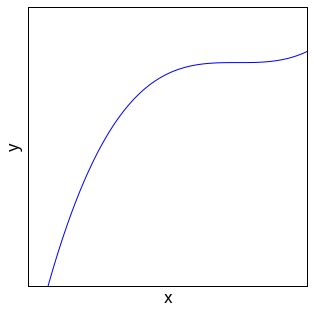
其曲线可能是这样的：

例如平方根多项式：

其曲线可能是这样的：

使用这些曲线进，相比一条直线，能够更加准确地对数据进行拟合。

不过这时候，对特征进行缩放或者归一，就非常重要。

例如三次多项式：

h_θ(x) = θ₀ + θ₁x + θ₂x² + θ₃x³

其实是可以看作：

h_θ(x) = θ₀ + θ₁x₁ + θ₂x₂ + θ₃x₃

如果说x = 1000，那么：

x₁ = x¹ = 1000
x₂ = x² = 1000 000
x₃ = x³ = 1000 000 000

这样的特征数据范围就非常大，如果不对特征进行归一化处理，那么梯度下降需要迭代的次数就非常多。

2 更加快速地收敛

怎么判定梯度下降算法有没有正常运行呢？

我们期盼的结果，是梯度下降算法步骤每一次的执行，得到的代价函数的值都应该是更小的。

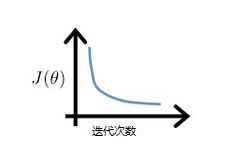
也就是说随着迭代运行的次数增加，代价函数的曲线应该是向下走的，例如这样：

如果运行的结果是这样的：

那就意味着，随着迭代次数的增加，代价函数的值反而越来越大了。

这就违背了使用梯度下降算法的初衷——我们希望找到让代价函数最小的参数组合。

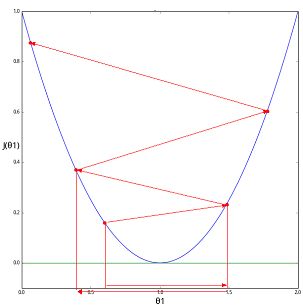
还记得之前在《机器学习笔记003 | 梯度下降算法》发的一个图片么：

学习速率α太大

因为学习速率α太大，所以随着算法的运行，得到的代价函数是越来越大的。

这时候，我们需要做的，就是要把学习速率α缩小。

当然也不能太小，如果太小，又需要执行非常多步才能找到答案：

学习速率α太小

那么怎么才能找到合适的学习速率α呢？

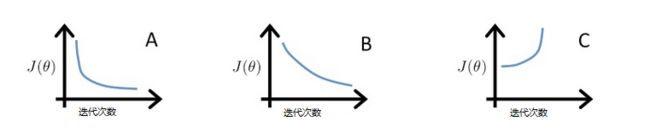
在此之前，我们可以先看看，对于代价函数来说，什么样的走势才是比较合适的：

在图C中，代价函数的结果是在上升的，所以学习速率α太大了。

图形A和图形B虽然都能够收敛，但是图形B显然收敛的速度要慢于图形A，也就是说图形B的学习速率α太小了。

在这三者中间，图形A的学习速率α是最合适的。

所以回到上面的问题，怎么寻找最合适的学习速率α？

我们可以进行多个范围的尝试，例如先 0.01, 0.1, 1 这样的一组学习速率。

然后把图形画出来，最终我们发现 0.1 可能对应着图形A， 0.01 可能对应着图形B，1可能对应着图形C，也就是说 0.1 是此时我们找到最合适的值。

然后以它为中心点，将学习速率重新调整为 0.03, 0.1, 0.3，再次进行尝试，如此反复。

我们想要做的，是通过不断的尝试来缩小学习速率α的范围，然后找到最合适或者相对合适的值。

文章转载自公众号：止一之路