【论文笔记】问答系统(一):基于图卷积(GCN)文本模型的跨模态信息检索
刚开始摸索NLP中的问答系统,于是对刚开始读的一些论文做了笔记,共享一下。笔记首次分享于公众号“专知”,为人工智能从业者服务,提供专业可信的人工智能知识与技术服务。有喜欢的朋友微信搜索“专知"?
Abstract
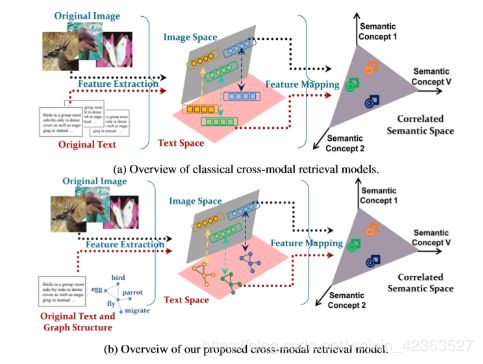
作者针对跨模态信息检索的耦合特征学习提出了一个双路径神经网络。其中的一条路径利用图卷积网络(GCN)进行基于图形表示的文本建模,另一条路径使用具有非线性层的神经网络。这个模型通过训练成对相似性损失函数来最大化匹配图文对的相似性,最小化不匹配对的相似性。实验显示,作者提出的模型相比最先进的方法有更出色的表现,而且精度提高了17%。
1 Introduction
随着网络科技的发展,在线多媒体的形势越来越多样化,用户获取的信息可能存在于不同的模态中,对此,传统的单模式信息检索技术就显得格外苍白,因此人们就逐渐采用跨模态信息检索的技术。
特征表示是跨模型信息检索的基石,对于图片,作者采用卷积神经网络进行预训练获取数据特征。对于文本,作者在文章中提到采用vector-space模型来学习高维语义,然而,用字频向量表示文本的时候,却没有考虑词之间关系。Zhang 等在他们的论文中,通过计算文本中所有词的word2vec向量的平均向量来表示文本。虽然这种词向量从相邻单词中获取更多信息,但它仍然忽略了文本中固有的全局结构信息,并且仅将该单词视为“flat”特征。
基于上述研究,为了获取文本词之间语义关系,作者采用图卷积(GCN)。基于GCN,作者提出了一个双路径神经网络,被命名为 Graph-In-Network (GIN),文本建模路径中采用GCN;图像建模路径中采用卷积神经网络,并采用成对相似性损失函数[Kumar BG et al., 2016]。
作者他们本文的主要工作有三点:
- 提出了一种跨模态检索模型,通过图卷积对文本数据进行建模,实现了不规则图形结构数据与常规网格结构数据之间的跨模型检索
- 模型可以共同学习文本和图像特征以及图文相似性度量,并提供了一种端到端的训练模式
- 在4个数据集上结果显示,他们的模型优于现有的方法
2 Methodology
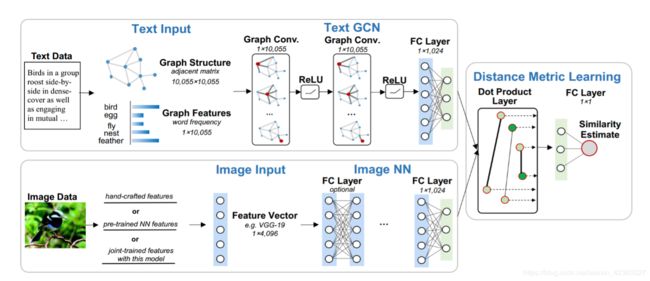
2.1 Text Modeling
文本建模中,有两个主要步骤,图结构 和GCN建模。
-
Graph Construction:
通过特征图将结构信息与语义信息结合在一起。假如给一组文本,从该语料库中获取words,并用 W = [ w 1 , w 2 , . . . , w n ] W=[w_1,w_2,...,w_n] W=[w1,w2,...,wn]表示,然后用预训练的word2vec嵌入表示。
我们用 G = ( V , E ) G=(V,E) G=(V,E)来表示图结构,每个顶点 v i ∈ V v_i ∈ V vi∈V对应一个词,每条边$e_{ij} ∈E $ 被定义为两字词之间的word2vec similarity:

这里, N k ( w ) N_k(w) Nk(w)表示K个最近邻居的集合,是通过计算词之间的 word2vec嵌入的cosine 的相似度。k是相邻参数的个数,试验中设置为8。图结构的参数用邻接矩阵 A ∈ R N × N A∈R^{N\times N} A∈RN×N。
对于图特征,我们将每个文本用词袋向量表示,词 w i w_i wi的频率用一个一维向量表示。这样,就将结构信息(词的相似关系)跟语义信息(词向量表示)在一个特征图中结合起来了。
-
GCN Modeling:
图卷积(GCN)将传统的卷积神经网络推广到不规则结构图中,这种思想基于图谱论。图卷积在频域作乘法处理,通过从频域到时域的逆变换获得特征图。假如给定一个文本, F i n F_{in} Fin表示图特征向量的输入, F o u t F_{out} Fout表示图卷积输出向量。首先, F i n F_{in} Fin要经过傅里叶变换,这个变换基于图拉普拉斯的[归一化][https://blog.csdn.net/StreamRock/article/details/82754539], L = I N − D − 1 / 2 A D − 1 / 2 L=I_N-D^{-1/2}AD^{-1/2} L=IN−D−1/2AD−1/2 , I N I_N IN 为单位矩阵, D D D 为图结构G的度矩阵。 L L L 进行特征分解, L = U Λ U T L=U Λ U^T L=UΛUT , U U U 为特征向量矩阵。Λ 为对角矩阵,其对角线上的元素为对应的特征值。对 F i n F_{in} Fin进行傅里叶变换:
[Defferrard et al., 2016] 提出了一个多项式滤波器 g θ g_\theta gθ:
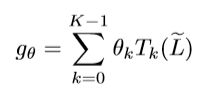
公式中, T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x T_k(x)=2xT_{k-1}(x)-T_{k-2}(x), T_0(x)=1, T_1(x)=x Tk(x)=2xTk−1(x)−Tk−2(x),T0(x)=1,T1(x)=x
![]()
λ m a x \lambda_{max} λmax为 L L L的最大特征值,因此可以将卷积计算表示为 F o u t = g θ F i n F_{out}=g_{\theta}F_{in} Fout=gθFin 。对于一个文本,第i个图特征输入 f i n , i ∈ F i n f_{in,i}∈F_{in} fin,i∈Fin 指的是顶点 v i v_i vi 的词频,第i个特征的输出 f o u t , i ∈ F o u t f_{out,i}∈F_{out} fout,i∈Fout 表示为:
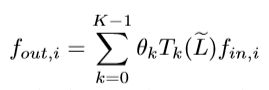
K作者在这里设置为3,就是卷积核的receptive filed,也就是说每次卷积会将中心顶点K-hop的特征进行加权求和。
作者提出的GCN模型中有2层图卷积,每层都采用ReLU激活函数,最后一层全连接层的维度与文本维度相同。
2.2 Image Modeling
图模型中,作者采用了一组全连接层,经过实验发现,模型中仅保留最后一层没有进行特征微调的语义映射层效果最好。
2.3 Objective Function
双路径模型(GIN)的最后一层,将前面两条路径的输出作为输入进行点乘运算,其输出为文本对的相似性分数。作者定义的损失函数,通过最大化匹配对的平均相似分数 u + u^+ u+,最小化非匹配对的平均相似分数 u − u^- u− ,同时最小化匹配对的相似性分数的方差 σ 2 + \sigma^{2+} σ2+ 和非匹配对的相似性分数方差 σ 2 − \sigma^{2-} σ2−, 将损失降到最小:
![]()
λ , m \lambda,m λ,m 为参数,实验中分别为0.6,0.35。
文本 T i T_i Ti 与图片 I i I_i Ii 是同一类时:
![]()
文本 T i T_i Ti 与图片 I i I_i Ii 是不同类时:
![]()
其中,作者选择 Q 1 + Q 2 = 200 Q_1 + Q_2 = 200 Q1+Q2=200 个文本对进行训练。
3 Experimental Studies
3.1 Datasets
作者分别在4个英文数据集( English Wikipedia, NUS-WIDE, Pascal VOC, and TVGraz)以及中文 Wikipedia 数据集上进行实验。
3.2 Evaluation and Implementation
基于4个数据集,实验同时对比12个模型,对实验结果MAP进行评估。实验设置40000个图文匹配的正样本与40000个不匹配的负样本,dropout为0.2,学习率为0.001,Adam优化器,正则化0.005,参数 λ , m \lambda,m λ,m 分别为0.6,0.35,进行50个epoch训练。
3.3 Experimental Results
- 文本查询图片实验中,在相同数据集上,GIN相比其他模型,MAP都要高,原因是模型通过图结构的形式表示出了词之间的语义关系。
- 图片查询文本的实验中,GIN似乎没有特别出色,原因在于作者采用的现成的图像特征向量,如果图像特征提取的神经网络用于模型中,实验结果会更好。
- 两组实验的平均MAP,GIN的结果相当好。
4 Conclusion
作者提出的跨模态检索模型(GIN)将不规则图结构的文本表示与图像结合,共同学习特征和语义空间。经过实验并对比其他数据集,作者提出的模型具有更好的性能。
GCN源码分析
代码结构:
gcn
||______________________init.py
||____ __inits.py
||__________layers.py
||___________metrics.py
||_________models.py
||_________train.py
||__________utils.py
def load_data(dataset_str):
names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph']
objects = []
for i in range(len(names)):
with open("data/ind.{}.{}".format(dataset_str, names[i]), 'rb') as f:
if sys.version_info > (3, 0):
objects.append(pkl.load(f, encoding='latin1'))
else:
objects.append(pkl.load(f))
x, y, tx, ty, allx, ally, graph = tuple(objects)
test_idx_reorder = parse_index_file("data/ind.{}.test.index".format(dataset_str))
test_idx_range = np.sort(test_idx_reorder)
if dataset_str == 'citeseer': #citeseer数据中含有离散的点,将其表示为零向量
test_idx_range_full = range(min(test_idx_reorder), max(test_idx_reorder)+1)
tx_extended = sp.lil_matrix((len(test_idx_range_full), x.shape[1]))
tx_extended[test_idx_range-min(test_idx_range), :] = tx
tx = tx_extended
ty_extended = np.zeros((len(test_idx_range_full), y.shape[1]))
ty_extended[test_idx_range-min(test_idx_range), :] = ty
ty = ty_extended
features = sp.vstack((allx, tx)).tolil()
features[test_idx_reorder, :] = features[test_idx_range, :]#获取特征
adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))#获取无向图
labels = np.vstack((ally, ty))
labels[test_idx_reorder, :] = labels[test_idx_range, :]
idx_test = test_idx_range.tolist()
idx_train = range(len(y))
idx_val = range(len(y), len(y)+500)
train_mask = sample_mask(idx_train, labels.shape[0])
val_mask = sample_mask(idx_val, labels.shape[0])
test_mask = sample_mask(idx_test, labels.shape[0])
y_train = np.zeros(labels.shape)
y_val = np.zeros(labels.shape)
y_test = np.zeros(labels.shape)
y_train[train_mask, :] = labels[train_mask, :]
y_val[val_mask, :] = labels[val_mask, :]
y_test[test_mask, :] = labels[test_mask, :]
return adj, features, y_train, y_val, y_test, train_mask, val_mask, test_mask#将特征归一化并转成元组形式
def preprocess_features(features)
#设计计算公式$D^{-1/2}(A+I)D^{-1/2}$
def normalize_adj(adj)
def preprocess_adj(adj)
#定义切比雪夫多项式
def chebyshev_polynomials(adj, k)
#定义一个Model基类
class Model(object)
#定义MLP
class MLP(Model)
#定义两层GCN,采用交叉熵损失与正则项
class GCN(Model)
#定义一个layer基类
class Layer(object)
#定义Dense Layer类
class Dense(Layer)
#定义GCN中,下面代码是实现公式$D^{-1}AXW+b$
class GraphConvolution(Layer):
……
supports = list()
for i in range(len(self.support)):
if not self.featureless:
pre_sup = dot(x, self.vars['weights_' + str(i)],
sparse=self.sparse_inputs)
else:
pre_sup = self.vars['weights_' + str(i)]
support = dot(self.support[i], pre_sup, sparse=True)
supports.append(support)
output = tf.add_n(supports)
# bias
if self.bias:
output += self.vars['bias']
return self.act(output)
f.support[i], pre_sup, sparse=True)
supports.append(support)
output = tf.add_n(supports)
# bias
if self.bias:
output += self.vars['bias']
return self.act(output)