吴恩达机器学习课后作业第一周ex1答案详解
吴恩达机器学习ex1
前言:此次机器学习是本人第一次接触matlab 所以以下的代码中会有对于一些matlab函数的解释
ex1_m:
Par1:

图中部分命令解释:
pause:表示程序执行到此处时停止,用于按任意键可以继续执行
上图函数 warmUpExercise() 函数表示求出一个 5 x 5 的单位矩阵
Part2:
Part2部分是对 ex1data1.txt文件中的样例来绘制相关的图像,直观的看出样例的分布情况

上图表示的是ex1data1.txt中的样例,第一列表示样例的特征值,第二列表示样例的结果
图中部分命令解释:
data = load(‘ex1data1.txt’):表示将ex1data1.txt中的数据以矩阵的形式存放在data中
X = data(:,2):表示将data中的第一列的全部的数据存放在X中
m = length(y):length()函数表示求取vector的长度,如何函数中的参数为矩阵,则只会求矩阵有多少列
plotData(X,y):

图中部分命令解释:
figure:表示创建一个绘图的窗口
plot():表示绘制一个2D图像,前两个参数X,Y的数据分别对应到2D图像中X和Y轴上的数据,rx中r表示使用red颜色,x表示以 ‘X’ 标志绘制点,‘MarkerSize’ 10 表示将点的大小设置为10
ylabel(‘Profit in $10000s’):表示在y轴附上说明
Part3:
Part3主要是利用梯度下降的方法求出最佳的theta,使得代价函数J的值最小
1、computeCost()用于计算代价函数J
根据ex1data1.txt对应的样例,我们设置hypothesis函数为:
h θ = θ T x = θ 0 + θ 1 x h_{\theta }=\theta ^{T}x=\theta _{0}+\theta _{1}x hθ=θTx=θ0+θ1x
代价函数为:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( X ( i ) ) − Y ( i ) ) 2 J\left( \theta \right) =\dfrac {1}{2m}\sum ^{m}_{i=1}\left( h_{\theta }\left( X^{\left( i\right) }\right) -Y^{\left( i\right) }\right) ^{2} J(θ)=2m1i=1∑m(hθ(X(i))−Y(i))2
computeCost()函数:

部分命令解释:
(X * thera - Y) .^2中的 .^2表示矩阵对应的每一个数都取平方值
sum():表示对矩阵中的每一个数求和
2、gradientDescent.m:用梯度下降的方法求最佳的theta值,使代价函数的值最小
利用梯度下降求theta的公式如下:
θ j : = θ j − α ∗ ∂ ∂ θ j J ( θ ) \theta _{j}:=\theta _{j}-\alpha \ast \dfrac {\partial }{\partial \theta _{j}}J\left( \theta \right) θj:=θj−α∗∂θj∂J(θ)
对theta求偏导数的过程如下:
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( θ T X ( i ) − y ( i ) ) x j ( i ) \dfrac {\partial }{\partial \theta _{j}}J\left( \theta \right) =\dfrac {1}{m}\sum ^{m}_{i=1}\left( \theta ^{T}X^{\left( i\right) }-y^{\left( i\right) }\right) x^{\left( i\right) }_{j} ∂θj∂J(θ)=m1i=1∑m(θTX(i)−y(i))xj(i)
gradientDescent函数如下:

使用梯度下降求出最佳的theta之后,利用plot函数画出theta拟合的图像:

图像如下:

之后利用求出的theta值就可以进行预测
Part4:
Part4主要对代价函数中各个参数进行可视化操作,观察各个参数对应的代价函数的值
代价函数J随参数theta变化的3D图像:

surf():绘制3D图像,theta0,theta1分别表示第一和第二个参数,J_val表示此时参数对应的代价函数值
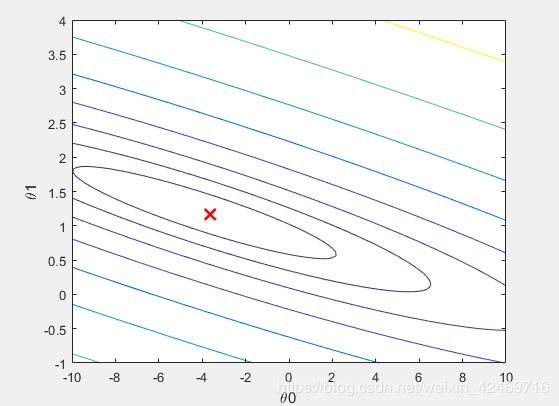
代价函数J随参数theta变化的等高线图像:

contour():用于绘制等高线图像
logspace(a,b,n):生成n个点,在10^a 和 10^b之间
ex1_multi.m:
Part1:
介绍:此部分主要是对示例的特征值进行特征收缩处理,使用的场景:当示例中的特征值相差的级别较大时,此时会导致梯度下降算法收敛的速度过于缓慢,比如下图中的数据,此时前两列为特征值,特征值1的数量级为10^ 3,而特征值2的数量级为10^1,此时就会造成梯度下降的速度过于缓慢,可以采用特征收缩的方法使其特征尺度都尽量收缩到[-1,1]之间。

特征收缩的公式:
x i = ( x i − u i ) σ i x_{i}=\dfrac {\left( x_{i}-u_{i}\right) }{\sigma_{i} } xi=σi(xi−ui)
上述公式中的 u i u_{i} ui指的是特征值 x i x_{i} xi的平均值, σ i \sigma_{i} σi指的是特征值 x i x_{i} xi 的标准差。
1、formalNormalize()函数
此函数用于进行特征收缩:

Part2:
此部分主要是根据经过特征收缩之后的特征值利用梯度下降的方法来求出最佳的 θ \theta θ 值,同时,此部分利用 plot函数画出代价函数J随迭次次数增加的变化曲线图,根据此曲线图,可以判断梯度下降的公式是否正确
1、gradientDescentMult()函数

上图中theta值的每次迭代利用了矩阵来求解,写成矩阵形式的迭代公式如下:
θ : = θ − α ∗ 1 m ∗ x T ∗ ( θ T x − y ) \theta := \theta - \alpha * \dfrac{1}{m} * x^{T} * \left( \theta^{T}x - y\right) θ:=θ−α∗m1∗xT∗(θTx−y)
代价函数J的变化曲线如下:

从上图中可以看出,梯度下降正常运行
Part3:
此部分主要是使用正规方程来求解最佳的 θ \theta θ值
正规方程如下:
θ = ( x T x ) − 1 x T y \theta = \left(x^{T}x\right)^{-1}x^{T}y θ=(xTx)−1xTy
上述公式的推导这位大佬已给出:正规方程 θ \theta θ推导详细过程
1、normalEqn():
![]()
使用上述代码就可以求解出最佳的 θ \theta θ值,之后就可以利用此值进行预测
正规方程与梯度下降的比较
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择适合的学习率 α \alpha α | 不需要 |
| 需要进行多次迭代 | 一次运算便可得出 |
| 当特征数量n较大时也能很好的适用 | 需要计算 ( x T x ) − 1 \left(x^{T}x\right)^{-1} (xTx)−1,当特征值n较大时,运算代价过大,因为矩阵逆的计算时间复杂度为 O ( n 3 ) O\left(n^{3}\right) O(n3),通常n小于10000时可以使用 |
| 适合于各种类型的模型 | 只适用于线性模型,不适用于逻辑回归模型等其他模型 |