主成分分析 (PCA) 的Python实现

一句话概括主成分分析

主成分分析是采取一种数学降维的方法，找出几个综合变量来代替原来众多的变量，使这些综合变量能尽可能地代表原来变量的信息量，而且彼此之间互不相关。这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。

---

主成分分析步骤

1. 对原始数据进行标准化处理
2. 计算标准化数据协方差矩阵
3. 求协方差矩阵的特征值和特征向量
4. 将特征值按照从大到小的顺序排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵
5. 将样本点投影到选取的特征向量上

---

Python代码实现

导入相关的Python库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

创建主成分分析类，包含函数 $fit()$ 和 $transform()$：

• $fit()$ 为pca模型训练函数，输入参数分别用来训练的原始数据（Dataframe格式）和设定的降维后特征数$k$
• $transform()$ 为模型拟合函数，将训练好的pca模型对需要转化的原始数据进行pca降维，输入参数为需要降维的Dataframe，输出值为pca降维后的Dataframe

class PCA:
    def __init__(self):
        self.val_ = []
        self.vec_ = np.array([])
        
    def fit(self, df, k):
        if k>df.shape[1]:
            print('k must lower than feature number')
        else:
            df_scale = (df - df.mean()) / df.std()      # z-score标准化
            df_cov = np.cov(df_scale.T)                 # 协方差矩阵
            val, vec = np.linalg.eig(df_cov)            # 协方差矩阵特征值、特征向量
            index = np.argsort(-val)[:k]                # 求出特征向量从大到小排列的索引
            val = val[index]                            # 特征值从大到小重新排列
            vec = vec[:,index]                          # 特征值相应的特征向量也重新排列
            self.val_, self.vec_ = val, vec
            
    def transform(self, df):
        col_names = df.columns
        final = np.dot(df-df.mean(), vec.T)             # m*n维的原始数据矩阵与n*k特征向量矩阵点乘即为降维后的结果
        return pd.DataFrame(final, columns=[str(i)+'_pca' for i in col_names])

为了验证算法是否成功实现PCA，创建数据进行验证
由于二维数据方便进行可视化，创建一个二维的Dataframe

x1=[2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]
x2=[2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9]
data = pd.DataFrame({'x1':x1, 'x2':x2})

进行PCA转换，为了方便可视化将降维后维度设为2，及与原始数据维度相同
得到PCA转换后的数据Dataframe，同时打印前k个特征值和特征向量

pca = PCA()
pca.fit(data,2)
data_pca = pca.transform(data)
print(pca.val_)
print(pca.vec_)

[1.92592927 0.07407073]
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]

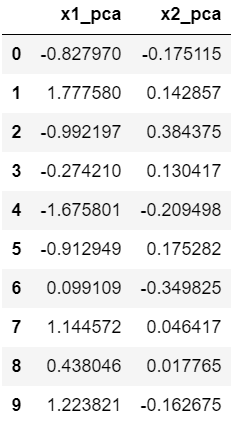
完成，成功对数据进行PCA转换！
从特征值可见，第一主成分（x1_pca）特征值占所有特征值总和的95%以上，囊括了绝大部分的信息

---

PCA结果可视化

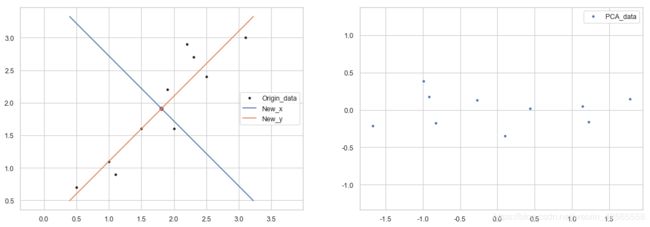
将结果可视化，分别查看原始数据、由特征向量构成的新的x轴、y轴、以及降维后的数据

x1_mean = data['x1'].mean()             # 新坐标轴原点x值
x2_mean = data['x2'].mean()             # 新坐标轴原点y值

vec_1 = pca.vec_[0]                     # 新坐标轴New_x单位向量
vec_2 = pca.vec_[1]                     # 新坐标轴New_y单位向量

sns.set(style='whitegrid')
plt.figure(figsize=(18,6), dpi=80)
plt.subplot(121)
plt.plot(data['x1'], data['x2'], '.k', label='Origin_data')
plt.plot(x1_mean, x2_mean, 'or')
plt.plot([x1_mean+vec_1[0]*2, x1_mean+vec_1[0]*-2], [x2_mean+vec_1[1]*2, x2_mean+vec_1[1]*-2], label='New_x')
plt.plot([x1_mean+vec_2[0]*-2, x1_mean+vec_2[0]*2], [x2_mean+vec_2[1]*-2, x2_mean+vec_2[1]*2], label='New_y')
plt.axis('equal')
plt.legend()

plt.subplot(122)
plt.plot(data_pca['x1_pca'], data_pca['x2_pca'], '.', label='PCA_data')
plt.axis('equal')
plt.legend()