新型冠状病毒SIR预测模型,MATLAB代码
What's the point of TOC
- SIR模型简介
- 数据获得和预处理
- 求解思路以及代码实现
- 结果展示
- 回复评论区
SIR模型简介
1、关于传染病的数学模型有哪些? - 知乎用户的回答 - 知乎
https://www.zhihu.com/question/367466399/answer/982558966
2、关于传染病的数学模型有哪些? - 酱紫君的回答 - 知乎
https://www.zhihu.com/question/367466399/answer/982597090
3、徐宝春. 基于SIR模型的SARS传染病研究[D]. 2019.
数据获得和预处理
数据获取方式为官方渠道。模型中的 I t I_t It和 R t R_t Rt的实际值由下列公式得到。

求解思路以及代码实现
易感人群初值 S 0 S_{0} S0难以估计,为待定量。动力学方程组中的 β \beta β和 γ \gamma γ同样为待定量。解决思路如下:
1、待定 S 0 S_{0} S0, β \beta β和 γ \gamma γ。目标函数为误差函数(见4),使用遗传算法寻找其最小值。
2、输入初值条件:第0天时的易感人数 S 0 S_0 S0,感染人数 I 0 I_0 I0和恢复人数 R 0 R_0 R0。
3、求解SIR模型的控制方程,获得第1~n天的SIR预测值:其为常微分方程组(ODE),可使用龙格库塔4阶方法。
4、求出实际值与预测值的误差。这部分误差由两部分构成,感染人数 I t I_t It和恢复人数 R t R_t Rt。而且由于数据源的滞后性和消息来源的不同,需要自行调整权重值。
遗传算法的目标函数代码:
function ra=optSIR(X)
% beta=0.00002;
% gamma=1/20;
beta=X(1)/1e6;
gamma=X(2)/1e2;
S0=X(3)*1e4;
x0=[S0,25,2];
ts=0:1:300;
[t,x] = ode45(@(t,x) SIRModel(t,x,beta,gamma), ts, x0);
I =[7621 5768 4696 3747 2857 2364 2042 1721 1458 578 526 502 440 227 169 41 28 27 25];
R =[730 616 446 362 358 275 219 184 132 120 92 70 55 31 29 21 17 14 02];
T =[35 34 33 32 31 30 29 28 27 26 25 24 23 20 19 17 16 15 0];
intensifiedPoint=15;
iP=intensifiedPoint;
omega=[iP iP iP iP 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
eps_I=0;eps_R=0;
for i=1:length(T)
eps_I=eps_I+omega(i)*(x(T(i)+1,2)-I(i))^2/I(i)^2;
eps_R=eps_R+omega(i)*(x(T(i)+1,3)-R(i))^2/R(i)^2;
% eps_I=eps_I+omega(i)*(x(T(i)+1,2)-I(i))^2;
% eps_R=eps_R+omega(i)*(x(T(i)+1,3)-R(i))^2;
end
omegaI=1e0;
ra=(omegaI*sqrt(eps_I)+sqrt(eps_R))/length(T);
IsPlot=0;
if IsPlot==1
plot(t,x(:,1),'k',t,x(:,2),'r',t,x(:,3),'b');hold on
xlabel('时间/天');
ylabel('人数');
legend('S','I','R');
plot(T,I,'ro');hold on
plot(T,R,'bo');hold off
end
end
function y=SIRModel(t,x,beta,gamma)
y=[-beta*x(1)*x(2),beta*x(1)*x(2)-gamma*x(2),gamma*x(2)]';
end
clear
IsPlot=1;
ra=[24.77762843006681 0.019410894953088675 0.7805747296079624];
beta=ra(1)*1e-6;
gamma=ra(2)*1e-2;
S0=ra(3)*1e4;
x0=[S0,25,2];
ts=0:1:300;
[t,x] = ode45(@(t,x) SIRModel(t,x,beta,gamma), ts, x0);
I =[7621 5768 4696 3747 2857 2364 2042 1721 1458 578 526 502 440 227 169 41 28 27 25];
R =[730 616 446 362 358 275 219 184 132 120 92 70 55 31 29 21 17 14 02];
I=I/S0;R=R/S0;
T =[35 34 33 32 31 30 29 28 27 26 25 24 23 20 19 17 16 15 0];
% The data is from Wuhan city only. The data source cannot be revealed because it is related to sensitive word (Wuhan Wei Jian Wei and Hubei WJW).
if IsPlot==1
figure
x=x/S0;
plot(t,x(:,1),'k',t,x(:,2),'r',t,x(:,3),'b');hold on
xlabel('时间/天');
ylabel('比例');
plot(T,I,'ro');hold on
plot(T,R,'bo');hold off
legend('易感人群','感染人群预测值','康复人群预测值','感染人群实际值','康复人群实际值');
axis([0,300,0,1])
end
function y=SIRModel(t,x,beta,gamma)
y=[-beta*x(1)*x(2),beta*x(1)*x(2)-gamma*x(2),gamma*x(2)]';
end
结果展示
数据量不大的时候,可以看出拟合效果不错。
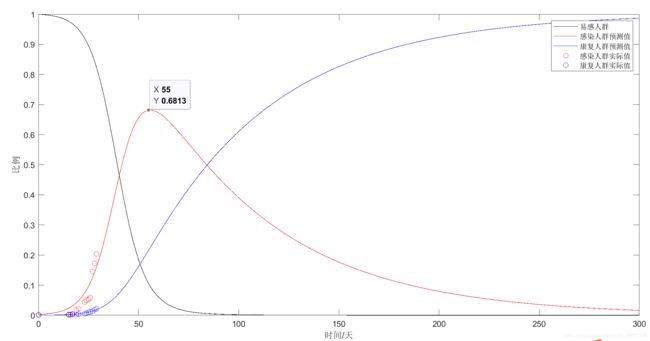
数据量较大的时候,可以看出拟合的效果不是特别好。
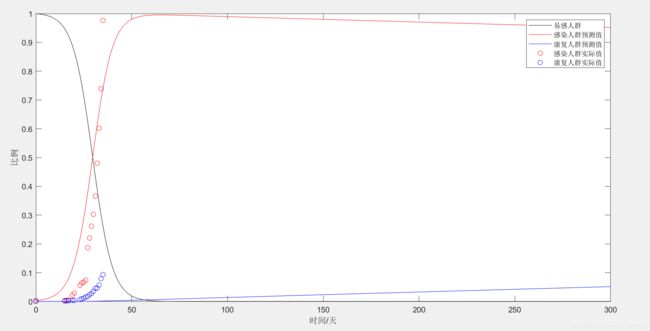
原因主要为:
1、S0的估计对误差的影响较大。预测图1的S0为10000人,预测图2的S0为7805人。
2、统计数据的滞后性。
3、I、R的计算方法可能不适合。
4、模型可能不适合。
回复评论区
Q1: S0怎么修改?
A1: 画图代码的S0变量,在第3行或者第6行
Q2: 遗传算法的代码解释?
A2: 简单说两句,MATLAB里面使用最优化方法主要有两种方法:1.图形化界面(本文使用的方法)。有个叫optimization的工具箱,点开就好,不过一些设置会比较奇葩。详情百度。2.在m文件中运行对应的函数。具体参见MATLAB的help,确实是个好东西。


