[引擎搭建记录] 延迟渲染管线与PBR(下)

这篇文章接着上篇讲述PBR相关的理论

github地址： https://github.com/MrySwk/GravityEngine （目前渲染部分代码乱七八糟，之后要重构一次）

图形库用的是DirectX12，目前引擎已经完成了基本的界面浏览功能、延迟管线、模型加载以及PBR，效果图如下

基于物理的渲染

PBR这个东西，真说要讲可能也轮不到我这个萌新来讲，因此这篇文章只是我个人对PBR的一些简单的理解和复述，也就是说会尽量地“讲人话”，在这个基础上，最好结合一些专业的资料来看，达到更好的理解效果。本人才疏学浅，如果有什么错误请指出。

首先关于PBR的理论，推荐这篇

https://learnopengl.com/PBR/Theory
可以看这个目录下的跟PBR有关的这四篇

以及浅墨的这个专栏，里面有一系列PBR相关的内容 https://zhuanlan.zhihu.com/p/53086060

上面那四篇是讲的最清楚的，如果认真看完基本上就能把程序写出来了，里面是给了代码的，虽然是opengl但是翻译成dx也不难。

那么接下来就可以开始谈PBR了，PBR就是一个光照模型，我这个引擎里实现的是最简单的PBR，也就是和虚幻里的做法基本上是一模一样的，我们可以回忆一下，经典的光照模型里面，漫反射是Lambert，镜面反射是Blinn-Phong，环境光是c*(1-AO)，而PBR，则是换了个更好看的模型，漫反射依然是Lambert（不过多除了个Pi），镜面反射是Cook-Torrance，环境光是IBL（Image-Based Lighting）。

预备知识

接下来就要不可避免地谈到反射方程了

Lo就是出射光强，${\omega }_i$是入射的立体角，${\omega }_o$是出射的立体角，p是顶点位置，Li点乘法线n，这个可以理解成入射的光强乘以兰伯特余弦，那么剩下的$f_r$，就是我们待会要讨论的主角，表示在p点这个位置，入射方向到出射方向光的反射比例。

接下来我们重新审视一遍这个式子，光线从各个方向入射，入射的能量会均匀分摊到照射到的面积上，所以要乘一个兰伯特余弦，也就是点乘一个法线，然后剩下的入射光强乘以入射和出射的比例，得到的其实就是这个光贡献的出射的光强，然后把所有方向来的光贡献的光强积分，就得到了最后的光强，这个积分是在p点法线为中心的半球上进行的。

那么问题来了，这个出射光和入射光的比例$f_r$是多少？这个函数就是BxDF，在我们实现的这个PBR模型里面，用的是BRDF（bi-directional reflectance distribution function，双向反射分布函数），如下

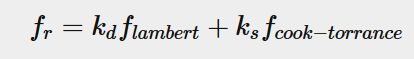
这个式子可以这样理解，反射光分为两部分，一部分是漫反射，一部分是镜面反射，刚刚说过lambert就是漫反射部分，cook-torrance就是镜面反射部分，那环境光呢？环境光后面会提，这里我们先关注漫反射和高光这两个部分。
$f_{lambert}$就是兰伯特反射分布函数，$f_{cook-torrance}$是高光部分的反射分布，然后有$k_d=1-k_s$，这里$k_d$应该理解成漫反射（d）的占比，而相应的$k_s$就是镜面反射（s）的占比，也就是说如果我们要把反射的光拆成diffuse和specular这两部分，我们要保证能量守恒。（其实这个$k_s$是包含在Cook-Torrance里面的，没必要写出来，但是为了强调能量守恒，还是放在上面了）（然后$k_d$一般也还要乘个(1-metal)，为了方便理解，先不要在意这个）

再说BRDF，BRDF就是出射与入射的比例，也就是$\frac{L_o}{E_i}$（注意单位），除了BRDF以外，还有其他的模型，如BSDF、BTDF、BSSRDF等，这些模型考虑了次表面散射等等，而游戏中用的最多的是BRDF，也就是只考虑反射，接下来我们可以具体看这个BRDF的内容。

漫反射

漫反射是兰伯特，式子很简单，如下

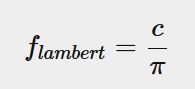
兰伯特的反照率就是一个常量，也就是albedo贴图上采样得到的值，但是和以前的兰伯特比，PBR里多除了一个$\pi$，为什么要除呢，其实这个地方除个$\pi$是保证能量守恒，因为我们的c是从贴图里面采样出来的，那么范围是在0到1之间的，但是实际上要能量守恒，c不能够大于$\frac{1}{\pi }$，证明如下
所以这里除个$\pi$，就是把[0,1]范围归一化到[0,$\frac{1}{\pi }$]，以前的不除的做法，是无法保证能量守恒的。这样是保证了全部的漫反射不会超过总能量，实际上还乘了个kd，则是保证了漫反射和镜面反射不会超过总能量。

镜面反射

PBR的镜面反射是Cook-Torrance，这部分内容是重头戏，先看结果

分子部分

分子包含了三个部分，D、F、G，首先看D。
D是Normal Distribution Function，简称NDF，中文应该叫法线分布函数（注意上面那篇的中文翻译里翻译成了正态分布函数，这是不合适的），如下

这个式子又称为Trowbridge-Reitz GGX，描述的是法线关于半角向量h和法线n的分布，其中$\alpha$是描述粗糙度的量，具体的可以根据实际情况来选择，虚幻的是$\alpha =roughnes{s}^2$（好像之前看到frostbite是用的粗糙度四次方，有待确认），我这里用的是和虚幻一样的。

需要注意的一点是，这个NDF不是概率密度函数，这个式子的归一是要乘上微平面法线m的$cos\theta$的，这里不展开讲了，后面还会提到。

然后第二个部分F，这个部分就是我们熟悉的菲涅尔了，用的依然是Schlick近似，如下

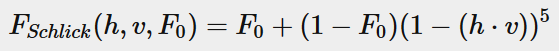
菲涅尔描述的是，光的入射角和法线夹角小的时候，反射率小，而夹角大的时候，反射率大，也就是说，菲涅尔描述的其实是镜面反射光的占比，也就是上面提到的$k_s$，是包含在这个BRDF里的，不需要单独写出来。
然后我这里用的不是这个版本，而是Epic提出的拟合版本

这个的好处是稍微比算power快点，不过也就是说得用exp2()这个函数来算，不然应该没啥意义。
具体出处可以看这里
https://cdn2.unrealengine.com/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf

最后就是几何部分G，这里要先提到Schlick GGX，如下

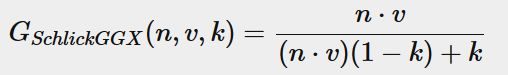
这部分的物理含义是，光线被崎岖不平的物体表面遮挡后，所剩下来的量，如图

其中的k应该这样计算

这其中的$\alpha$是粗糙度。我们现在在算直接光部分，所以就用$\frac{(\alpha +1{)}^2}{8}$。
然后从图上可以看出，光线入射的时候有一次遮蔽，出射到眼睛的时候还有一次遮蔽，这两次分别跟入射矢量和出射矢量有关，所以最终的几何部分是

一次是用v（view）算一次使用l（light）算。

这样，分子里DFG三个部分就已经讲完了，我们可以这样理解，光入射后，根据F知道有多少光被镜面反射了，然后乘上D，即有多少成分反射到了视角的方向，然后乘上G，也就是被遮挡了多少，就是出射光强，不过这只是分子，我们还没考虑分母，我们要像刚才漫反射那样，保证能量守恒，也就是说纯镜面反射的能量不能超过入射的总能量，所以还要除掉一个分母。

配平

配平的这部分，大部份讲PBR的文章里都没有给出具体解释，给我当时的学习也造成了困难，所以为了区别于其他讲PBR的文章，我会把我找到的解释写在这里。

可以参考 https://twvideo01.ubm-us.net/o1/vault/gdc2017/Presentations/Hammon_Earl_PBR_Diffuse_Lighting.pdf

为了归一化，我们首先要找出能量是怎么守恒的，这就需要先了解一下微平面理论，上面的资料里也都提了，这里我们只考虑一个纯镜面反射的情况。这种情况下我们的BRDF是$k{\delta }_m(H,m)$，k就是我们要找的系数，然后接下来要看一张图。（这张图是从某盗版书里拍下来的，，正版太贵实在买不起）

看右边这张，这张图告诉我们，微平面中只有一些部分会对视角，也就是出射立体角接受的光线做出贡献，图上正的部分和负的部分会抵消，所以实际上宏观平面在出射立体角上的投影和微平面在出射立体角上的投影是相等的，都是总面积乘上一个$cos\theta$。

然后接下来就可以列出能量守恒的式子了，我们有
$${\int }_{\Omega }\rho \cdot cos{\theta }_{V}dV=1$$

BRDF是出射和入射的比值（先别去追究单位），那么各方向出射的能量加起来和入射能量的比值为1，就是守恒。

接下来会有巨大多计算，懒得打公式和画图，我就用手写了

这样一来镜面反射部分也保证能量守恒了。

回到反射方程

现在我们再来看一次反射方程，用上面的式子来展开，有

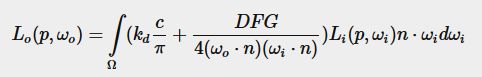
那么现在这个式子的含义就已经基本上可以理解了，注意右边镜面反射部分把$k_s$拿掉了，因为这里F就是$k_s$了。

环境光

接下来是PBR里的环境光，用的是IBL，也就是基于图像的光照，其实一般的很老的图形学基础入门书里也都会提到用cubemap的采样和f0来渲染对环境的反射，那PBR的做法与传统有什么不同呢？答案自然是PBR的做法会更加的物理。事实上我们不太可能在游戏里事实地对物体周遭进行采样然后实时计算积分，这个代价太大了，即使是不物理的，也就是摆个cubemap采样摄像头，然后不积分，虽然可以实时跑，但是代价也大得可怕，所以其实现在的做法依然是搞一张固定的环境贴图，事先算好，然后实时跑地时候只做小量的运算。

首先环境光还是老样子，拆成两部分，漫反射和镜面反射

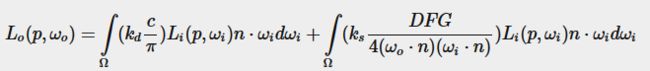
和经典的一个常量c乘上1-AO不同，这里我们不再是用常量来表示环境光的辐射度，而是真正真正的把它算出来，但是，问题来了，这个难度是非常大的，和刚才的直接光计算不同，这次是要真正的积分了。
刚才的直接光，我们都是用加的，因为无论是点光源，还是平行光，都只从一个方向来，这种情况下积分就是做加法，但是环境光就不同了，我们从整个环境（也就是一张cubemap）上面获得光照信息，可以认为这个光源是个面光源，是有面积的，所以环境光的计算就是把上面的式子积分算出来。

漫反射

漫反射部分如下

原理和直接光一模一样，只是要把整个环境cubemap积一次分，实际上我们积的是以法线n为中心的半球，这里好像也没什么好说的，直接算就是了，结果如下

右边是积分结果，看起来像是一张模糊过了的环境贴图，可以理解。但是我们不能用高斯模糊来代替这个积分运算，因为我们做这件事的意义就是让光照更加物理，那么追求物理上的正确是理所应当的。

这个积分过程我也看了一些别人的实现，似乎都是等间距采样，为什么不蒙特卡洛呢，我猜可能是为了加快收敛速度吧，我最后写的也是等间距采样，但是用蒙特卡洛积分也是一样的， 总之看到结果比较平滑，不是很噪了就可以了。

镜面反射

镜面反射相比之下就比较复杂了，因为运算量会远远大于漫反射，如下

这个过程跟刚才的有点区别，我们还要考虑粗糙度，但是这样的话就太复杂了，所以一般我们只采样个五六张，每一张对应不同粗糙度，然后三线性插值得到最终采样结果（是的，这样就不物理了）。然后我在实现的时候用了虚幻提出的一个近似算法，Split Sum，把这个积分拆成两个部分

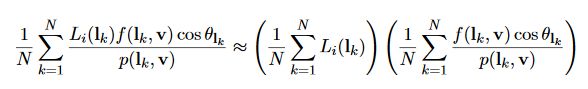
现在的非常多做法都是这样做的，首先看左边部分，叫Pre-Filtered Environment Map，计算不同粗糙度如下。

然后这个部分的积分，我看很多地方给的实现，依然不是用标准的蒙特卡洛，而是用的准蒙特卡洛算法，有什么区别呢，这种做法是产生一系列不那么随机的、分布还算比较均匀的假的随机数，来加快收敛速度

这就是蒙特卡洛常用的伪随机序列和伪蒙特卡洛的low-discrepancy序列的区别，可以想象右边的收敛会快很多。
（具体代码会贴在后面。）

然后剩下右边部分，

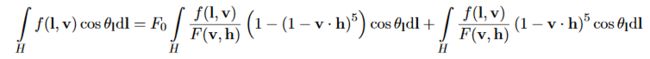
这一部分是定死的，可以预先算好，算出来之后得到这样一张贴图

这个就是虚幻著名的look-up texture（LUT），这张图我就没有亲手去算了，到处都能找到，就直接嫖了。

这张图用法是用roughness和NdotV去采样，然后积分结果等于(F * envBRDF.x + envBRDF.y)，具体可以看代码。

代码实现

其实上面给的四篇参考里已经有非常完整的实现了，使用opengl写的，这里我贴一下我用dx12写的代码，其实这种文章里好像也不合适贴太多代码，所以就只把关键部分贴一下了

首先是事前准备，算好环境贴图：

Irradiance预积分

static const float PI = 3.14159265359;

TextureCube gCubeMap		: register(t0);
SamplerState basicSampler	: register(s0);

cbuffer cbPerObject : register(b0)
{
	float4x4 gWorld;
	float4x4 gTexTransform;
	uint gMaterialIndex;
	uint gObjPad0;
	uint gObjPad1;
	uint gObjPad2;
};

cbuffer cbPass : register(b1)
{
	float4x4 gViewProj;
	float3 gEyePosW;
	float roughnessCb;
};

struct VertexOut
{
	float4 PosH		: SV_POSITION;
	float3 PosL		: POSITION;
};

float4 main(VertexOut pin) : SV_TARGET
{
	float3 irradiance = float3(0.0f, 0.0f, 0.0f);

	float3 normal = normalize(pin.PosL);
	float3 up = float3(0.0, 1.0, 0.0);
	float3 right = cross(up, normal);
	up = cross(normal, right);

	float sampleDelta = 0.025f;
	float numSamples = 0.0f;
	for (float phi = 0.0f; phi < 2.0f * PI; phi += sampleDelta)
	{
		for (float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
		{
			// spherical to cartesian (in tangent space)
			float3 tangentSample = float3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
			// tangent space to world
			float3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * normal;
			
			irradiance += gCubeMap.Sample(basicSampler, sampleVec).rgb * cos(theta) * sin(theta);
			numSamples++;
		}
	}
	irradiance = PI * irradiance * (1.0f / numSamples);

	return float4(irradiance, 1.0f);
}

Prefilter Map积分

static const float PI = 3.14159265359;

TextureCube gCubeMap		: register(t0);
SamplerState basicSampler	: register(s0);

cbuffer cbPerObject : register(b0)
{
	float4x4 gWorld;
	float4x4 gTexTransform;
	uint gMaterialIndex;
	uint gObjPad0;
	uint gObjPad1;
	uint gObjPad2;
};

cbuffer cbPass : register(b1)
{
	float4x4 gViewProj;
	float3 gEyePosW;
	float roughnessCb;
};

float RadicalInverse_VdC(uint bits)
{
	bits = (bits << 16u) | (bits >> 16u);
	bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
	bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
	bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
	bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
	return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}

float2 Hammersley(uint i, uint N)
{
	return float2(float(i) / float(N), RadicalInverse_VdC(i));
}

float3 ImportanceSampleGGX(float2 Xi, float3 N, float roughness)
{
	float a = roughness * roughness;

	float phi = 2.0 * PI * Xi.x;
	float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
	float sinTheta = sqrt(1.0 - cosTheta * cosTheta);

	// from spherical coordinates to cartesian coordinates
	float3 H;
	H.x = cos(phi) * sinTheta;
	H.y = sin(phi) * sinTheta;
	H.z = cosTheta;

	// from tangent-space vector to world-space sample vector
	float3 up = abs(N.z) < 0.999 ? float3(0.0, 0.0, 1.0) : float3(1.0, 0.0, 0.0);
	float3 tangent = normalize(cross(up, N));
	float3 bitangent = cross(N, tangent);

	float3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
	return normalize(sampleVec);
}

struct VertexOut
{
	float4 PosH		: SV_POSITION;
	float3 PosL		: POSITION;
};

float4 main(VertexOut pin) : SV_TARGET
{
	float roughness = roughnessCb;
	const uint NumSamples = 1024u;
	float3 N = normalize(pin.PosL);
	float3 R = N;
	float3 V = R;

	float3 prefilteredColor = float3(0.f, 0.f, 0.f);
	float totalWeight = 0.f;
	for (uint i = 0u; i < NumSamples; ++i)
	{
		float2 Xi = Hammersley(i, NumSamples);
		float3 H = ImportanceSampleGGX(Xi, N, roughness);
		float3 L = normalize(2.0f * dot(V, H) * H - V);
		float NdotL = max(dot(N, L), 0.0f);
		if (NdotL > 0.f)
		{
			prefilteredColor += gCubeMap.Sample(basicSampler, L).rgb * NdotL;
			totalWeight += NdotL;
		}
	}

	prefilteredColor = prefilteredColor / totalWeight;

	return float4(prefilteredColor, 1.0f);
}

然后是光照计算

#ifndef _LIGHTING_HLSLI
#define _LIGHTING_HLSLI

#define MAX_DIRECTIONAL_LIGHT_NUM 4
#define MAX_POINT_LIGHT_NUM 16
#define MAX_SPOTLIGHT_NUM 16

static const float MIN_ROUGHNESS = 0.0000001f;
static const float F0_NON_METAL = 0.04f;
static const float PI = 3.14159265359f;

struct SpotLight
{
	float4 Color;
	float4 Direction;
	float3 Position;
	float Range;
	float SpotlightAngle;
};

struct DirectionalLight
{
	float4 AmbientColor;
	float4 DiffuseColor;
	float3 Direction;
	float Intensity;
};

struct PointLight
{
	float4 Color;
	float3 Position;
	float Range;
	float Intensity;
	float3 Padding;
};

cbuffer externalData : register(b0)
{
	DirectionalLight dirLight[MAX_DIRECTIONAL_LIGHT_NUM];
	PointLight pointLight[MAX_POINT_LIGHT_NUM];
	float3 cameraPosition;
	int pointLightCount;
	int dirLightCount;
}

float Attenuate(float3 position, float range, float3 worldPos)
{
	float dist = distance(position, worldPos);
	float numer = dist / range;
	numer = numer * numer;
	numer = numer * numer;
	numer = saturate(1 - numer);
	numer = numer * numer;
	float denom = dist * dist + 1;
	return (numer / denom);
}

// Lambert diffuse 
float3 LambertDiffuse(float3 kS, float3 albedo, float metalness)
{
	float3 kD = (float3(1.0f, 1.0f, 1.0f) - kS) * (1 - metalness);
	return (kD * albedo / PI);
}

// GGX (Trowbridge-Reitz)
float SpecDistribution(float3 n, float3 h, float roughness)
{
	float NdotH = max(dot(n, h), 0.0f);
	float NdotH2 = NdotH * NdotH;
	float a = roughness * roughness;
	float a2 = max(a * a, MIN_ROUGHNESS);

	float denomToSquare = NdotH2 * (a2 - 1) + 1;

	return a2 / (PI * denomToSquare * denomToSquare);
}

float3 Fresnel_Schlick(float3 v, float3 h, float3 f0)
{
	float VdotH = max(dot(v, h), 0.0f);
	return f0 + (1 - f0) * pow(1 - VdotH, 5);
}

float3 Fresnel_Epic(float3 v, float3 h, float3 f0)
{
	float VdotH = max(dot(v, h), 0.0f);
	return f0 + (1 - f0) * exp2((-5.55473 * VdotH - 6.98316) * VdotH);
}

// Fresnel term - Schlick approx.
float3 Fresnel(float3 v, float3 h, float3 f0)
{
	return Fresnel_Epic(v, h, f0);
}

float3 FresnelSchlickRoughness(float3 v, float3 n, float3 f0, float roughness)
{
	float NdotV = max(dot(v, n), 0.0f);
	float r1 = 1.0f - roughness;
	return f0 + (max(float3(r1, r1, r1), f0) - f0) * pow(1 - NdotV, 5.0f);
}

// Schlick-GGX 
float GeometricShadowing(float3 n, float3 v, float3 h, float roughness)
{
	// End result of remapping:
	float k = pow(roughness + 1, 2) / 8.0f;
	float NdotV = max(dot(n, v), 0.0f);

	// Final value
	return NdotV / (NdotV * (1 - k) + k);
}

// Cook-Torrance Specular
float3 CookTorrance(float3 n, float3 l, float3 v, float roughness, float metalness, float3 f0, out float3 kS)
{
	float3 h = normalize(v + l);

	float D = SpecDistribution(n, h, roughness);
	float3 F = Fresnel(v, n, f0);
	float G = GeometricShadowing(n, v, h, roughness) * GeometricShadowing(n, l, h, roughness);
	kS = F;
	float NdotV = max(dot(n, v), 0.0f);
	float NdotL = max(dot(n, l), 0.0f);
	return (D * F * G) / (4 * max(NdotV * NdotL, 0.01f));
	//return (D * F * G) / (4 * max(dot(n, v), dot(n, l)));
}

float3 AmbientPBR(float3 normal, float3 worldPos,
	float3 camPos, float roughness, float metalness,
	float3 albedo, float3 irradiance, float3 prefilteredColor, float2 brdf, float shadowAmount)
{
	float3 f0 = lerp(F0_NON_METAL.rrr, albedo.rgb, metalness);
	float ao = 1.0f;
	float3 toCam = normalize(camPos - worldPos);

	float3 kS = FresnelSchlickRoughness(toCam, normal, f0, roughness);
	float3 kD = float3(1.0f, 1.0f, 1.0f) - kS;
	kD *= (1.0f - metalness);

	float3 specular = prefilteredColor * (kS * brdf.x + brdf.y);
	float3 diffuse = irradiance * albedo;

	float3 ambient = (kD * diffuse + specular) * ao;

	return ambient;
}

float3 DirectPBR(float lightIntensity, float3 lightColor, float3 toLight, float3 normal, float3 worldPos, float3 camPos, float roughness, float metalness, float3 albedo, float shadowAmount)
{
	float3 f0 = lerp(F0_NON_METAL.rrr, albedo.rgb, metalness);
	float ao = 1.0f;
	float3 toCam = normalize(camPos - worldPos);
	//float atten = Attenuate(light.Position, light.Range, worldPos);
	float3 kS = float3(0.f, 0.f, 0.f);
	float3 specBRDF = CookTorrance(normal, toLight, toCam, roughness, metalness, f0, kS);
	float3 diffBRDF = LambertDiffuse(kS, albedo, metalness);

	float NdotL = max(dot(normal, toLight), 0.0);

	return (diffBRDF + specBRDF) * NdotL * lightIntensity * lightColor.rgb * shadowAmount;
}

这里的光照衰减我用的是虚幻的，具体可以看上面贴的那篇虚幻的文章

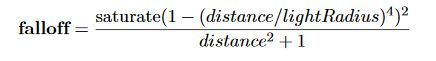
然后是直接光pass

float4 main(VertexToPixel pIn) : SV_TARGET
{
	float4 packedAlbedo = gAlbedoTexture.Sample(basicSampler, pIn.uv);
	float3 albedo = packedAlbedo.rgb;
	float3 normal = gNormalTexture.Sample(basicSampler, pIn.uv).rgb;
	float3 worldPos = gWorldPosTexture.Sample(basicSampler, pIn.uv).rgb;
	float roughness = gOrmTexture.Sample(basicSampler, pIn.uv).g;
	float metal = gOrmTexture.Sample(basicSampler, pIn.uv).b;


	float3 finalColor = 0.f;
	float shadowAmount = 1.f;

	for (int i = 0; i < pointLightCount; i++)
	{
		shadowAmount = 1.f;
		float atten = Attenuate(pointLight[i].Position, pointLight[i].Range, worldPos);
		float lightIntensity = pointLight[i].Intensity * atten;
		float3 toLight = normalize(pointLight[i].Position - worldPos);
		float3 lightColor = pointLight[i].Color.rgb;

		finalColor = finalColor + DirectPBR(lightIntensity, lightColor, toLight, normalize(normal), worldPos, cameraPosition, roughness, metal, albedo, shadowAmount);
	}
	
	for (int i = 0; i < dirLightCount; i++)
	{
		float shadowAmount = 1.f;
		float lightIntensity = dirLight[i].Intensity;
		float3 toLight = normalize(-dirLight[i].Direction);
		float3 lightColor = dirLight[i].DiffuseColor.rgb;

		finalColor = finalColor + DirectPBR(lightIntensity, lightColor, toLight, normalize(normal), worldPos, cameraPosition, roughness, metal, albedo, shadowAmount);
	}

	return float4(finalColor, 1.0f);
}

间接光pass

float4 main(VertexToPixel pIn) : SV_TARGET
{
	float4 packedAlbedo = gAlbedoTexture.Sample(basicSampler, pIn.uv);
	float3 albedo = packedAlbedo.rgb;
	float3 normal = gNormalTexture.Sample(basicSampler, pIn.uv).rgb;
	float3 worldPos = gWorldPosTexture.Sample(basicSampler, pIn.uv).rgb;
	float roughness = gOrmTexture.Sample(basicSampler, pIn.uv).g;
	float metal = gOrmTexture.Sample(basicSampler, pIn.uv).b;
	float shadowAmount = 1.f;

	float3 viewDir = normalize(cameraPosition - worldPos);
	float3 prefilter = PrefilteredColor(viewDir, normal, roughness);
	float2 brdf = BrdfLUT(normal, viewDir, roughness);
	float3 irradiance = skyIrradianceTexture.Sample(basicSampler, normal).rgb;

	float3 finalColor = AmbientPBR(normalize(normal), worldPos,
		cameraPosition, roughness, metal, albedo,
		irradiance, prefilter, brdf, shadowAmount);
	return float4(finalColor, 1.0f);
}

最后进入后处理，这一步我现在只做了HDR到LDR的色调映射和gamma校正

float4 main(VertexToPixel pIn) : SV_TARGET
{
	float3 direct = gDirectLight.Sample(basicSampler, pIn.uv).rgb;
	float3 ambient = gAmbientLight.Sample(basicSampler, pIn.uv).rgb;

	float directIntensity = 1.0f;
	float ambientIntensity = 1.0f;
	float3 totalColor = direct * directIntensity + ambient * ambientIntensity;

	totalColor = totalColor / (totalColor + float3(1.f, 1.f, 1.f));
	totalColor = saturate(totalColor);
	float3 gammaCorrect = lerp(totalColor, pow(totalColor, 1.0 / 2.2), 1.0f);
	return float4(gammaCorrect, 1.0f);
}

最后就输出到屏幕上得到结果了。

结语

写着写着不知不觉就一万多字了，写的过程中我也加深了一下对PBR的理解，接下来一段时间我可能会把引擎代码重构一下，现在我比较想知道的是渲染器部分和管其他逻辑的引擎内核部分要解耦的话要具体落实到哪些细节上，可能会需要动手清理下代码，以免以后想加个opengl进来会受太多苦。
这篇文章中间很可能漏了一些小东西忘了提，一开始写的时候想到了好多，写着写着就都不记得了，如果有什么错误欢迎批评指正23333。