图像处理———图像的均值滤波、方框滤波和高斯滤波的原理及实现
一、线性滤波和非线性滤波
- 常用的线性滤波:均值滤波、高斯滤波、盒子滤波、拉普拉斯滤波等等,通常线性滤波器之间只是模版系数不同。
- 非线性滤波:利用原始图像跟模版之间的一种逻辑关系得到结果,如最值滤波器,中值滤波器。比较常用的有中值滤波器和双边滤波器。
二、方框滤波(盒子滤波)
均值滤波是盒子滤波归一化的一种特殊情况。
1、应用:可以说,一切需要求某个邻域内像素之和的场合,都有方框滤波的用武之地,比如:均值滤波、引导滤波、计算Haar特征等等。
2、优势:速度快。它可以使复杂度为O(MN)的求和,求方差等运算降低到O(1)或近似于O(1)的复杂度,也就是说与邻域尺寸无关了,有点类似积分图,但是比积分图更快(与它的实现方式有关)。
opencv函数:
void boxFilter( InputArray src, OutputArray dst, int ddepth,
Size ksize, Point anchor = Point(-1,-1),
bool normalize = true,
int borderType = BORDER_DEFAULT );
原理
用一个内核和图像进行卷积

其中
![]()
可见,归一化了就是均值滤波;不归一化则可以计算每个像素邻域上的各种积分特性,方差、协方差,平方和等等。
代码实现(python)
使用一个归一化卷积框,用卷积框覆盖区域所有像素的平均值来代替中心元素。可以使用cv2.blur()和cv2.boxFilter()来实现, 我们需要设定卷积框的宽和高。同样是一个矩阵。
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('1024.jpg')
blur = cv2.blur(img,(5,5))
while(1):
cv2.imshow('image',img)
cv2.imshow('blur',blur)
k=cv2.waitKey(1)
if k == ord('q'):#按q键退出
break
cv2.destroyAllWindows()
效果如图 上面是原图,下面是平滑后的图,可以看到下面的图被平滑过了。
三、均值滤波
根据冈萨雷斯书中的描述,均值模糊可以模糊图像以便得到感兴趣物体的粗略描述,也就是说,去除图像中的不相关细节,其中“不相关”是指与滤波器模板尺寸相比较小的像素区域,从而对图像有一个整体的认知。即为了对感兴趣的物体得到一个大致的整体的描述而模糊一幅图像,忽略细小的细节。
均值滤波本身存在着固有的缺陷,即它不能很好地保护图像细节,在图像去噪的同时也破坏了图像的细节部分,从而使图像变得模糊,不能很好地去除噪声点。特别是椒盐噪声。
均值滤波是上述方框滤波的特殊情况,均值滤波方法是:对待处理的当前像素,选择一个模板,该模板为其邻近的若干个像素组成,用模板的均值(方框滤波归一化)来替代原像素的值。公式表示为:
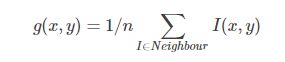
g(x,y)为该邻域的中心像素,n跟系数模版大小有关,一般3 * 3邻域的模板,n取为9,如:

当然,模板是可变的,一般取奇数,如5 * 5,7 * 7等等。
注:在实际处理过程中可对图像边界进行扩充,扩充为0或扩充为邻近的像素值。
扩展内容见这篇博客
四、高斯滤波
高斯滤波是一种线性平滑滤波器,对于服从正态分布的噪声有很好的抑制作用。在实际场景中,我们通常会假定图像包含的噪声为高斯白噪声,所以在许多实际应用的预处理部分,都会采用高斯滤波抑制噪声,如传统车牌识别等。
高斯滤波和均值滤波一样,都是利用一个掩膜和图像进行卷积求解。不同之处在于:均值滤波器的模板系数都是相同的为1,而高斯滤波器的模板系数,则随着距离模板中心的增大而系数减小(服从二维高斯分布)。所以,高斯滤波器相比于均值滤波器对图像个模糊程度较小,更能够保持图像的整体细节。
二维高斯分布公式:
![]()
代码实现只需将上面的代码改成
blur = cv2.GaussianBlur(img,(5,5),0)
更多滤波内容见这篇文档