用matlab实现假设性检验T检验(葡萄酒评价)
2012建模的题目是要求对葡萄酒品质进行评价,第一问是两组葡萄酒的评价有没有显著性差异,用的是统计学中的假设T检验。matlab代码如下:
% 清空环境变量
clear all
clc
%导入数据
X1=xlsread('2012A_T1_processed.xls', 'T1_red_grape', 'D3:M272');
X2=xlsread('2012A_T1_processed.xls', 'T2_red_grape', 'D3:M272');
X3=xlsread('2012A_T1_processed.xls', 'T1_white_grape', 'D3:M282');
X4=xlsread('2012A_T1_processed.xls', 'T2_white_grape', 'D3:M282');
%% 红葡萄酒T检验计算过程
[m1,n1]=size(X1);
K1=27;
% 计算每个样品的总得分
for i=1:K1
for j=1:n1
SX1(i,j)=sum(X1(10*i-9:10*i,j));
SX2(i,j)=sum(X2(10*i-9:10*i,j));
end
end
% 计算每组样品得分的均值
for i=1:K1
Mean1(i)=mean(SX1(i,:));
Mean2(i)=mean(SX2(i,:));
end
% 计算检验值
for i=1:K1
S1(1,i)=(sum((SX1(i,:)-Mean1(i)).^2)+sum((SX2(i,:)-Mean2(i)).^2))/(n1*(n1-1));
T1(1,i)=(Mean1(i)-Mean2(i))/(sqrt(S1(1,i)));
end
AT_R=abs(T1);
M_AT_R=mean(AT_R);
%% 白葡萄酒T检验计算过程
[m2,n2]=size(X3);
K2=28;
% 计算每个样品的总得分
for i=1:K2
for j=1:n2
SX3(i,j)=sum(X3(10*i-9:10*i,j));
SX4(i,j)=sum(X4(10*i-9:10*i,j));
end
end
% 计算每组样品得分的均值
for i=1:K2
Mean3(i)=mean(SX3(i,:));
Mean4(i)=mean(SX4(i,:));
end
% 计算检验值
for i=1:K2
S2(1,i)=(sum((SX3(i,:)-Mean3(i)).^2)+sum((SX4(i,:)-Mean4(i)).^2))/(n2*(n2-1));
T2(1,i)=(Mean3(i)-Mean4(i))/(sqrt(S2(1,i)));
end
AT_W=abs(T2);
M_AT_W=mean(AT_W);
%% 结果显示与比较
a=2.102; % T(0.05,2,18)=2.101
b=2.878; % T(0.01,2,18)=2.878
set(gca,'linewidth',2)
% 红酒结果
for i=1:K1
Ta1(i)=a;
Tb1(i)=b;
end
t1=1:K1;
subplot(2,1,1);
plot(t1,AT_R,'*k-',t1,Ta1,'r-',t1,Tb1,'-.b', 'LineWidth', 2)
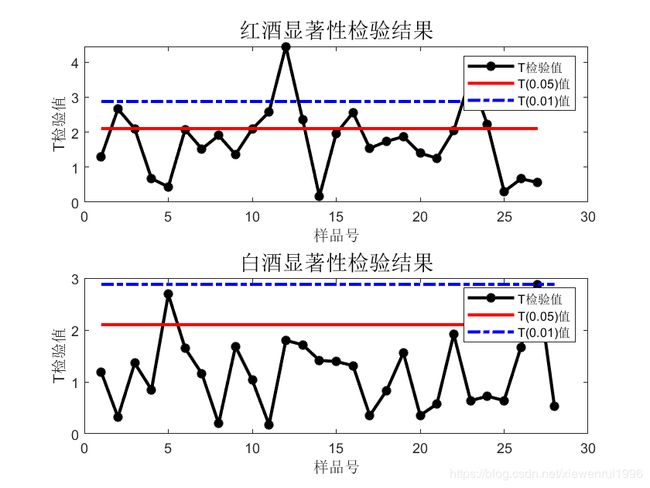
title('红酒显著性检验结果','fontsize',14)
legend('T检验值', 'T(0.05)值', 'T(0.01)值')
xlabel('样品号'), ylabel('T检验值')
% 白酒结果
for i=1:K2
Ta2(i)=a;
Tb2(i)=b;
end
t2=1:K2;
subplot(2,1,2);
plot(t2,AT_W,'*k-',t2,Ta2,'r-',t2,Tb2,'-.b', 'LineWidth', 2)
title('白酒显著性检验结果','fontsize',14)
legend('T检验值', 'T(0.05)值', 'T(0.01)值')
xlabel('样品号'), ylabel('T检验值')
% 显示平均检验结果
disp(['两组品酒师对红酒的平均显著性T检验值:' num2str(M_AT_R)]);
disp(['两组品酒师对白酒的平均显著性T检验值:' num2str(M_AT_W)]);输出:
两组品酒师对红酒的平均显著性T检验值:1.7539
两组品酒师对白酒的平均显著性T检验值:1.1641
查表可知,t(0.05,2.18)=2.101,t(0.01,2.18)=2.878。按照t检验的步骤,可得到下面的结论:
①两组品酒师对红葡萄酒和白葡萄酒的评价效果差异都不显著
②对白葡萄酒效果的评价差异小于红葡萄酒。