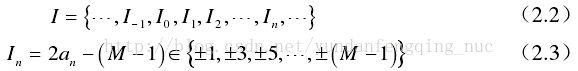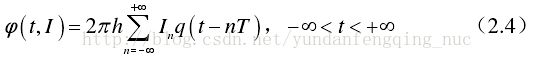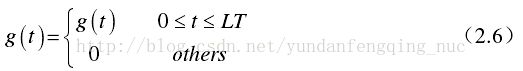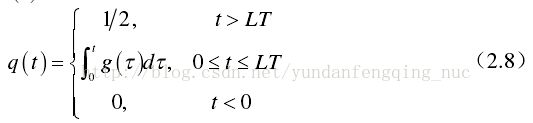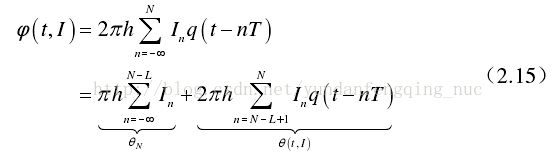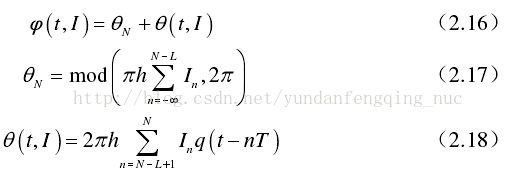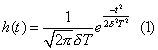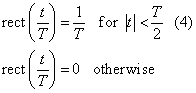GMSK调制解调（一）

一、连续相位调制原理

1、CPM信号模型

CPMC信号的实数域数学表达式：

               

上式中，A表示符号能量，fc表示载波频率，I为发送的码元数据

              

T表示码元周期，承载了待发送的码元信息，表示CPM基带信号的时变相位函数，

为信号的初始相位。与PSK信号基带相位取有限的离散值不同，CPM基带信号的相位

是时间的连续函数。下面给出CPM信号的连续相位函数的表达式：

                 

上式中，h为CPM信号的调制指数，它决定了每个符号周期内CPM信号的相位变化量。调制指数h越大，一个符号周期内相位的变化越大，时域和频域上越容易区分：q(t)称为相位成形脉冲函数，由一个持续时间有限的脉冲函数g(t)积分得到：

                  

所以脉冲函数g(t)也称为频率成形脉冲。

                   

频率脉冲函数g(t)仅在区间[0,LT]有非零值，其中L称为关联长度，且频率脉冲函数g(t)具有一下特点：

                  

因此，相位成形脉冲函数q(t)满足以下关系：

          

由上面各式可得，调制指数h、频率成形脉冲函数g(t)、关联长度L和基带符号的进制数M，共同决定了CPM基带信号的相位随时间变化的规律，选择不同的调制指数可以得到不同的连续相位调制信号，并且这一大类CPM信号具有相似的性质。从式（2.4）的积分形式可以看出，相位成形脉冲函数q(t)是时间的连续函数，这保证了CPM基带信号相位函数

的连续性，而且频率脉冲函数g(t)还决定了相位脉冲函数q(t)的波形；从式（2.8）可以看出，关联长度L影响了相位脉冲函数的编码特性，L越大引入的编码效应越明显。

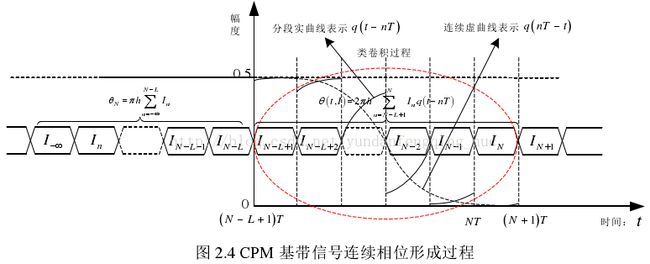
2、CPM连续相位形成

CPM信号本质上仍是相位调制，CPM调制是将原始待发送二进制信息映射为CPM基带信号的连续相位，然后与载波进行相位调制。CPM基带信号相位形成过程是所有发送码元符号对相位成形脉冲函数q(t)的线性加权和，从表达式（2.4）可以看出，的形成过程与卷积的过程类似。因此，可以将形成过程看成是所有待发送码元符号与相位成形脉冲函数q(t)的类似卷积，即用相位成形脉冲函数q(t)对待发送的基带码元符号进行成形滤波，使其带限。下面对CPM信号的基带相位进行详细分析。

将在第N个码元符号周期内进行分析，N为整数，且，即当前时刻。重写CPM基带信号的连续相位表达式如下：

由式（2.8）可知，脉冲成形函数q(t)在t<=0时为0，在t>=LT时取固定值1/2，所以式（2.14）可以展开乘如下形式：

其中，是CPM基带信号的固定相位部分，称为固定相位，是区间（负无穷，N-L]内所有码元符号线性累加和对应的相位，其值在一个符号周期内固定不变，为h*pi的整数倍；是CPM基带信号连续变化的部分，称为关联相位，是当前L个码元符号与相位脉冲的时变部分进行类卷积得到的。CPM基带信号相位成形过程如图所示，可以表示成：

二、GMSK调制实现

在MSK信号的基础上，为了改善信号的旁瓣衰减性能，人们提出了在MSK调制器前端增加一个滤波器进行预调制的设想，引出了最小高斯频移键控（GMSK）的思想。双极性脉冲序列在通过高斯低通滤波器后，其信号波形更加平滑，经MSK调制器调制后，产生的调制信号的相位路径更加平滑，功率谱的旁瓣衰减性能更好。下文主要讲述GMSK调制的实现及Matlab仿真。

                                       

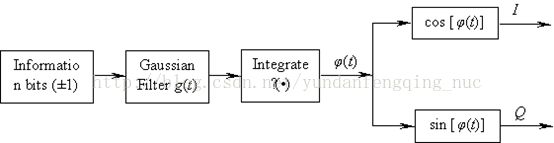
                                                                          图2.5 GMSK调制器的实现

图2.5给出了GMSK调制器的原理框图。GMSK调制中的高斯滤波器通常是由滤波器的BT乘积、3db带宽B和符号持续时间T决定的。高斯滤波器的脉冲响应为

                                                 

                                          

其中，

                                                                    

发送的信息比特bi（0/1）差分编码后变化为符号ai = +/-1。这些符号然后经过脉冲响应为g(t)的滤波器滤波

                                                                   

其中，表示卷积，

                                                                  

调制信号的相位为：

                                                                 

GMSK调制中h=1/2。

                                     

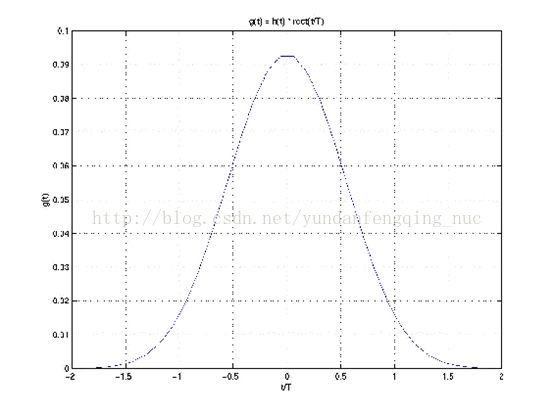
                                                                           图2.6 

从图2.6中可以看出，尽管脉冲响应函数g(t)的定义域为负无穷到正无穷，但是在|t|>2T区间上可以忽略，所以

假定|t|>2T区间上g(t)=0。由公式（3）可知，g(t)是非因果，不可实现的。所以假定|t|>2T区间上g(t)=0，将g(t)延时2T使得g(t)变成因果的。

Mtlab代码：

clc;
clear all;
close all;

burst = sign(randn(1 , 1000));

Tb = 1/19200;
OSR= 16;
BT = 0.3;

Ts = Tb/OSR;

PTV = -2*Tb:Ts:2*Tb;
RTV = -Tb/2:Ts:Tb/2;

sigma = sqrt(log(2))/(2*pi*BT); 
gauss = (1/(sqrt(2*pi)*sigma*Tb))*exp(-PTV.^2/(2*sigma^2*Tb^2)); 

rect = 1/(2*Tb)*ones(size(RTV));

G_TEMP = conv(gauss,rect);


% TRUNCATING THE FUNCTION TO 3xTb

G = G_TEMP(OSR+1:4*OSR); 

% TRUNCATION IMPLIES THAT INTEGRATING THE FREQUENCY PULSE
% FUNCTION WILL NOT EQUAL 0.5, HENCE THE RE-NORMALIZATION
G_FUN = (G-G(1))./(2*sum(G-G(1)));


% CALCULATE RESULTING PHASE PULSE
Q_FUN = cumsum(G_FUN);

参考文献：

1 http://www.embedded.com/print/4142719

2 《数据链物理层 CPM 波形调制解调技术研究与实现》 重庆大学硕士学位论文，作者：郭金超。

3 《突发 GMSK 信号分析与解调技术的研究与实现》 国防科技大学硕士学位论文，作者：朱磊。