简学lingo(四)——实例篇
本片将会接着上篇实例来写,如要参照可以看下上篇的http://blog.csdn.net/yzu_120702117/article/details/38453791
如有句法上的问题可以参照我之前总结的基础篇,传送门:http://blog.csdn.net/yzu_120702117/article/details/38444485和http://blog.csdn.net/yzu_120702117/article/details/38415153
6、最优选择问题
某钻井队要从10个可供选择的井位中确定5个钻井探油,使总的钻探费用为最小。若10个井位的代号为s1,s2,...,s10,相应的钻探费用c1,c2,...,c10为5,8,10,6,9,5,7,6,10,8.并且井位选择上要满足下列限制条件:
(1) 或选择s1和s7,或选择钻探s9;
(2) 选择了s3或s4就不能选s5,或反过来也一样;
(3) 在s5,s6,s7,s8中最多只能选两个.
试建立这个问题的整数规划模型,确定选择的井位。
取0-1变量s_i,若s_i=1,则表示选取第i个井,若s_i=0,则表示不选取第i个井。建立数学模型如下:
解决的代码如下
model:
sets:
variables/1..10/:s,cost;
endsets
data:
cost=5 8 10 6 9 5 7 6 10 8;
enddata
min=@sum(variables:cost*s);
(s(1)+s(7)-2)*(s(9)-1)=0; !约束条件
s(3)*s(5)+s(4)*s(5)=0;
@sum(variables(i)|i#ge#5 #and# i#le#8:s(i))<=2;
@sum(variable:s)=5;
@for(variables:@bin(s));
end
7.运输加选址问题
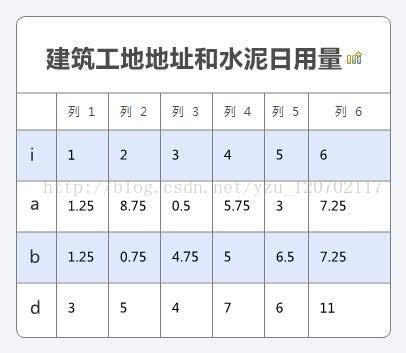
某公司有六个建筑工地,位置坐标(ai,bi)(单位:公里),水泥日用量di(单位:吨)
(1)现有2个料场,位于A(5,1),B(2,7),记(xj,yj),及,2,日存储量ej各有20吨。假设工地和料场之间有直线道路,制定每天的供应计划,即从A,B两料场分别向工地运送水泥,是得总的吨公里数最小,其中Cij表示i工地从j料场运来的水泥量。则可以建立模型
这个模型可以这样解答
model:
sets:
demand/1..6/:a,b,d;
supply/1..2/:x,y,e;
link(demand,supply):c;
endsets
data:
a=1.25 8.75 0.5 5.75 3 7.25;
b=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
x=5 2;
y=1 7;
e=20 20;
enddata
min=@sum(link(i,j):c(i,j)*@sqrt((a(i)-x(j))^2+(b(i)-y(j))^2)); !目标函数
@for(demand(i):@sum(supply(j):c(i,j))=d(i));
@for(supply(j):@sum(demand(i):c(i,j))<=e(j));
end
(2)改建两个新料场,需要确定新料场位置(xj,yj)和运量cij,在其他条件不变下使总公里数最小。模型与上面的一样,位置变量变为料场位置(xj,yj),变为非线性优化问题。
model:
sets:
demand/1..6/:a,b,d;
supply/1..2/:x,y,e;
link(demand,supply):c;
endsets
data:
a=1.25 8.75 0.5 5.75 3 7.25;
b=1.25 0.75 4.75 5 6.5 7.75;
d=3 5 4 7 6 11;
e=20 20;
enddata
init: !这里对x,y赋初值
x=5 2;
y=1 7;
endinit
[obj]min=@sum(link(i,j):c(i,j)*@sqrt((a(i)-x(j))^2+(b(i)-y(j))^2));!目标函数;
@for(demand(i):@sum(supply(j):c(i,j))=d(i));
@for(supply(j):@sum(demand(i):c(i,j))<=e(j));
@for(supply:@free(x);@free(y));
end
7.选址问题
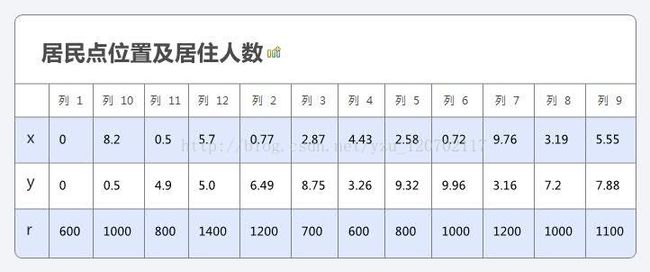
某海岛上有12个主要的居民点,每个居民点的位置(用平面坐标x,y表示,单位km)和居住人数(r)如下表所示。现在准备在海岛上建一个服务中心为居民提供各种服务,那么服务中心应该建在那里?
假设建在(a,b)处最合理。建立模型
求解这个模型:
MODEL:
SETS:
VAR/1..12/:X,Y,R;
ENDSETS
DATA:
X=0 8.20 0.50 5.70 0.77 2.87 4.43 2.58 0.72 9.76 3.19 5.55;
Y=0 0.50 4.90 5.00 6.49 8.76 3.26 9.32 9.96 3.16 7.20 7.88;
R=600 1000 800 1400 1200 700 600 800 1000 1200 1000 1100;
ENDDATA
MIN=@SUM(VAR:@SQRT((X-A)^2+(Y-B)^2)*R);
END
8.非线性整数规划:
model:
sets:
row/1..4/:b;
col/1..5/:c1,c2,x;
link(row,col):a;
endsets
data:
c1=1,1,3,4,2;
c2=-8,-2,-3,-1,-2;
a=1 1 1 1 1
1 2 2 1 6
2 1 6 0 0
0 0 1 1 5;
b=400,800,200,200;
enddata
max=@sum(col:c1*x^2+c2*x);
@for(row(i):@sum(col(j):a(i,j)*x(j))
9.婚配问题
10对年龄相当的青年,任意一对男女青年配对的概率pij见下表。试给出一个配对方案,使总的配对概率最大。
w1 w2 w3 w4 w5 w6 w7 w8 w9 w10
m1 0.5828 0.2091 0.4154 0.2140 0.6833 0.4514 0.6085 0.0841 0.1210 0.2319
m2 0.4235 0.3798 0.3050 0.6435 0.2126 0.0439 0.0158 0.4544 0.4508 0.2393
m3 0.5155 0.7833 0.8744 0.3200 0.8392 0.0272 0.0164 0.4418 0.7159 0.0498
m4 0.3340 0.6808 0.0150 0.9601 0.6288 0.3127 0.1901 0.3533 0.8928 0.0784
m5 0.4329 0.4611 0.7680 0.7266 0.1338 0.0129 0.5869 0.1536 0.2731 0.6408
m6 0.2259 0.5678 0.9708 0.4120 0.2071 0.3840 0.0576 0.6756 0.2548 0.1909
m7 0.5798 0.7942 0.9901 0.7446 0.6072 0.6831 0.3676 0.6992 0.8656

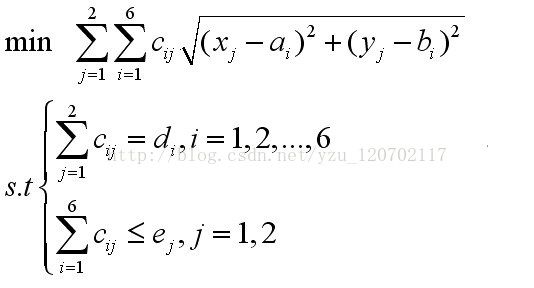

![[学习笔记]Lingo超经典案例大全 简学lingo(四)——实例篇_第5张图片](http://img.e-com-net.com/image/info8/4b01541d92334fdba1dcb25926406b91.jpg)