哈希表基本操作及其扩展

哈希表

• 哈希表的概念：
  
  • 哈希表本身是一个数组，其元素在数组中存放位置为：通过哈希函数使元素关键码和元素存储位置有一定的映射关系
• 哈希表的特点：
  
  • 搜索数组中某一元素时，可以通过该元素的关键码和存储位置的映射关系直接找到对应位置查看是否存在
  • 在数组中插入元素时，根据哈希函数计算出插入元素的位置并且在此位置存放
  • 存在哈希冲突：两个不同的元素通过哈希函数所映射的存储位置相同即为哈希冲突。例如：两个元素的关键字X != y,但有HashFunc(x) == HashFunc(y)

哈希冲突的解决方法

根据哈希表的特点可知，哈希冲突在所难免，虽然可以通过调整哈希函数来降低哈希函数的可能性，但还是不能完全避免哈希冲突，因此提出两种解决方案：

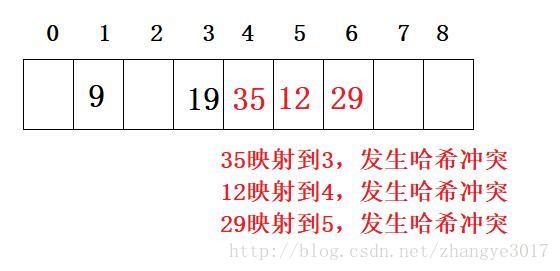
• 闭散列：开放地址法，即当哈希表未装满时，将待插入元素Key放在下一“空位”处，

  • “空位寻找”：线性探测和二次探测

  • 线性探测：从发生哈希冲突的位置挨着挨着向后找空位置，直到找到空位置，例如：

    

  • 二次探测：从哈希冲突的位置加上 i2 i 2 ，i=1,2,3,….例如：

    

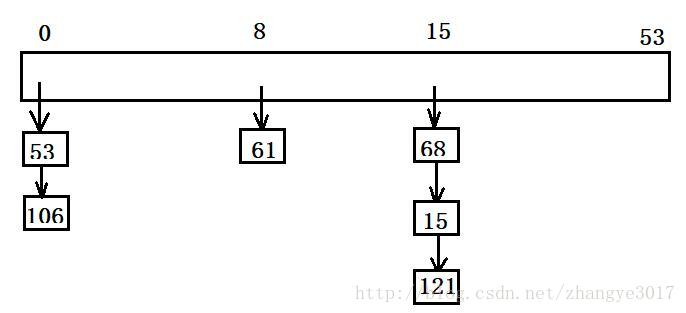
• 开散列：拉链法,首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中（如图）

  

基本操作

• 插入

  • 注意问题：
    （1）使用闭散列方法时扩容须满足的负载因子 （大于0.7）
    （2）使用开散列方法时扩容须满足的负载因子 （等于1）
    （3）扩容时将原哈希表中的内容存放至新表时，映射到新表的位置须重新计算
    （4）为了尽可能的避免哈希冲突，使用素数表对齐做哈希表的容量

• 删除

  • 注意问题：
    （1） 闭散列删除时只需要将其元素的状态改为删除即可
    （2）开散列在删除时需要将其所在节点进行删除，删除节点须注意是否为头节点

• 查找

  • 注意问题：
    （1）闭散列查找某一元素时，只须在存在状态的元素中寻找，如果状态该元素的关键码所映射的位置为空（EMPTY）或者删除（DELET）,表示该元素不存在
    （2）闭散列查找某一元素时，不仅需要在所映射的当前位置去找，还须在其所挂链表中寻找

代码实现

• 闭散列（开放地址）

#include
#include
#include

typedef enum Status
{
    EXITS,//存在
    EMPTY,//空
    DELETE,//删除
}Status;


typedef int KeyType;
typedef int ValueType;

typedef struct HashNode
{
    KeyType _key;
    ValueType _value;
    Status _status;
}HashNode;



typedef struct HashTable
{
    HashNode* _table;

    size_t _size;
    size_t _N;
}HashTable;

size_t GetNewN(size_t N);//获取容量
void HashTableInit(HashTable* hash);//初始化
int HashTableInsert(HashTable* hash, KeyType key, ValueType value);//插入
size_t HashFunc(size_t n, KeyType key);//获取坐标
void HashPrint(HashTable* hash);//打印
HashNode* HashTableFind(HashTable* hash, KeyType key);//查找
void HashTableRemove(HashTable* hash, KeyType key);//删除
void HashTableDestory(HashTable* hash);//销毁
void TestHash();




size_t GetNewN(size_t N)
{
    const int _PrimeSize = 28;
    static const unsigned long _PrimeList[_PrimeSize] =
    {
        53ul, 97ul, 193ul, 389ul, 769ul,
        1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
        49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
        1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
        50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
        1610612741ul, 3221225473ul, 4294967291ul
    };

    size_t i = 0;
    for (; i < _PrimeSize; ++i)
    {
        if (_PrimeList[i]>N)
        {
            return _PrimeList[i];
        }
    }

    return _PrimeList[_PrimeSize - 1];

}


//初始化
void HashTableInit(HashTable* hash,size_t N)
{
    //hash->_N = 3;
    hash->_N = N;
    hash->_size = 0;
    hash->_table = (HashNode*)malloc(sizeof(HashNode)*hash->_N);

    for (size_t i = 0; i < hash->_N; ++i)
    {
        hash->_table[i]._status = EMPTY;
    }

}



size_t HashFunc(size_t n,KeyType key )
{
    return  key%n;
}


void  IsFull(HashTable* hash)
{
    if (hash->_size * 10 / hash->_N >= 7)
    {
        //大于负载因子，进行扩容
        //并进行初始化

        //建立新的哈希表

        size_t newN = GetNewN( hash->_N);
        HashNode* newTable = (HashNode*)malloc(sizeof(HashNode)*newN);
        assert(newTable);
        for (size_t i = 0; i < hash->_N; ++i)
        {
            size_t newindex = HashFunc(newN,hash->_table[i]._key);
            while (newTable[newindex]._status == EXITS)
            {
                if (newindex == newN)
                    newindex = 0;

                ++newindex;
            }

            newTable[newindex] = hash->_table[i];
        }
        hash->_N = newN;
        free(hash->_table);
        hash->_table = newTable;
    }

}
//插入
int HashTableInsert(HashTable* hash, KeyType key, ValueType value)
{
    //判满并扩容
    IsFull(hash);

    size_t index = HashFunc(hash->_N, key);

    while (hash->_table[index]._status == EXITS)
    {
        //如果相等，不插入，直接返回
        if (hash->_table[index]._key == key)
            return -1;

        index++;
        //如果到最后，从头开始
        if (index == hash->_N)
        {
            index = 0;
        }
    }

    hash->_table[index]._key = key;
    hash->_table[index]._value = value;
    ++hash->_size;
    hash->_table[index]._status = EXITS;

    return 0;
}


//查找
HashNode* HashTableFind(HashTable* hash, KeyType key)
{
    assert(hash);
    size_t index = HashFunc(hash->_N, key);

    while (hash->_table[index]._status == EXITS)
    {
        if (hash->_table[index]._key == key)
            return &hash->_table[index];

        ++index;

        if (index == hash->_N)
            index = 0;


    }
    return NULL;

}


//删除
void  HashTableRemove(HashTable* hash, KeyType key)
{
    assert(hash);
    HashNode* tmp = HashTableFind(hash, key);
    if (tmp == NULL)
        return;

    tmp->_status = DELETE;
}

//销毁
void HashTableDestory(HashTable* hash)
{
    assert(hash);
    free(hash->_table);
    hash->_N = 0;
    hash->_size = 0;
}

void HashPrint(HashTable* hash)
{
    assert(hash);
    for (size_t i = 0; i < hash->_N; ++i)
    {
        if (hash->_table[i]._status == EXITS)
        {
            printf("[%d]->EX->%d  ", i, hash->_table[i]._key);
        }
        else if (hash->_table[i]._status == EMPTY)
        {
            printf("[%d]->EM  ",i);
        }
        else if (hash->_table[i]._status == DELETE)
        {
            printf("[%d]->DE  ", i);
        }
    }
    printf("\n\n");
}

• 开散列（拉链法）

#include
#include
#include
#include


typedef int KeyType;
typedef int ValueType;


typedef struct HashNode
{
    KeyType _key;
    ValueType _value;
    struct HashNode* _next;
}HashNode;

typedef struct HashTable
{
    HashNode** _tables;
    size_t _N;
    size_t _size;

}HashTable;


size_t GetNextPrimeNum(size_t N);//空间
void HashTableInit(HashTable* ht);//初始化
size_t HashFunc(size_t n, KeyType key);//计算坐标
HashNode* BuyHashNode(KeyType key, ValueType value);//创建节点
HashNode* HashTableFind(HashTable* ht, KeyType key);//查找
int HashTableRemove(HashTable* ht, KeyType key);//删除
void HashTablePrint(HashTable* ht);//打印
void HashTableDestory(HashTable* ht);//销毁
void TestHashTable();


size_t GetNextPrimeNum(size_t N)
{
    const int _PrimeSize = 28;
    static const unsigned long _PrimeList[_PrimeSize] =
    {
        53ul, 97ul, 193ul, 389ul, 769ul,
        1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
        49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
        1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
        50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
        1610612741ul, 3221225473ul, 4294967291ul
    };

    size_t i = 0;
    for (; i < _PrimeSize; ++i)
    {
        if (_PrimeList[i]>N)
        {
            return _PrimeList[i];
        }
    }

    return _PrimeList[_PrimeSize - 1];

}


void HashTableInit(HashTable* ht)
{
    ht->_N = GetNextPrimeNum(0);
    ht->_size = 0;
    ht->_tables = (HashNode**)malloc(sizeof(HashNode*)*ht->_N);
    assert(ht->_tables);
    memset(ht->_tables, NULL, sizeof(HashNode*)*ht->_N);


}

size_t HashFunc(size_t n, KeyType key)
{
    return  key%n;
}

//创建节点
HashNode* BuyHashNode(KeyType key, ValueType value)
{
    HashNode* node = (HashNode*)malloc(sizeof(HashNode));
    assert(node);
    node->_key = key;
    node->_value = value;
    node->_next = NULL;

    return node;
}

//插入
int HashTableInsert(HashTable* ht, KeyType key, ValueType value)
{
    assert(ht);

    if (ht->_N == ht->_size)
    {
        //获取下一个质数
        size_t newN= GetNextPrimeNum(ht->_N);
        //拷贝
        HashNode** NewTable = (HashNode**)malloc(sizeof(HashNode*)*newN);
        assert(NewTable);
        memset(NewTable, NULL, sizeof(HashNode*)*newN);

        for (size_t i = 0; i < ht->_N; ++i)
        {
            //新的位置
            HashNode* cur =ht->_tables[i];

            while (cur)
            {
                //进行头插
                size_t newindex = HashFunc(newN, cur->_key);
                HashNode* next = cur->_next;
                cur->_next = NewTable[newindex];
                 NewTable[newindex]=cur;
                 cur = next;
            }
        }
        ht->_N = newN;
        free(ht->_tables);
        ht->_tables = NewTable;
    }
    //获取位置
    size_t index = HashFunc(ht->_N, key);
    HashNode* cur = ht->_tables[index];
    while (cur)
    {
        if (cur->_key == key)//已经插入过不在插入
        {
            return -1;
        }
        cur = cur->_next;
    }


    HashNode* node = BuyHashNode(key, value);
    node->_next = ht->_tables[index];
    ht->_tables[index] = node;
    ++ht->_size;
    return 0;

}


//查找
HashNode* HashTableFind(HashTable* ht, KeyType key)
{
    assert(ht);
    size_t index = HashFunc(ht->_N,key);

    HashNode* cur = ht->_tables[index];

    while (cur)
    {
        if (cur->_key == key)
        {
            return cur;
        }
        cur = cur->_next;
    }

    return NULL;

}

//删除
int HashTableRemove(HashTable* ht, KeyType key)
{
    assert(ht);

    size_t index = HashFunc(ht->_N, key);

    //1.头节点
    //2.非头节点
    HashNode* cur = ht->_tables[index];
    HashNode* prev = cur;


    while (cur)
    {
        if (cur->_key == key)
        {
            if (prev == cur)
            {
                //头节点
                ht->_tables[index] = cur->_next;
            }
            else
            {
                //不是头节点
                prev->_next = cur->_next;
            }

            free(cur);
            return 0;
        }
        prev = cur;
        cur = cur->_next;
    }
    return -1;
}


//销毁
void HashTableDestory(HashTable* ht)
{
    assert(ht);
    free(ht->_tables);
    ht->_tables = NULL;
    ht->_N = 0;
    ht->_size = 0;
}


//打印
void HashTablePrint(HashTable* ht)
{
    assert(ht);

    for (size_t i = 0; i < ht->_N; ++i)
    {
        HashNode* cur = ht->_tables[i];
        while (cur)
        {
            printf("[%d]->%d ", i, cur->_key);
            cur = cur->_next;
        }

    }
    printf("\n\n");
}

哈希扩展

• 扩展一（位图）

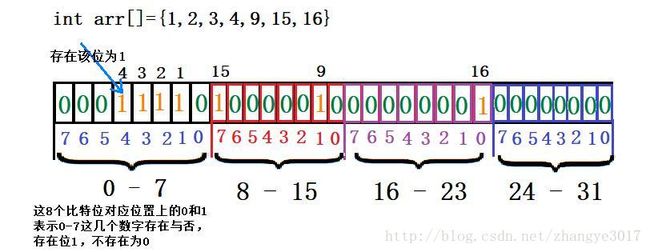
  • 位图理解：，位图是利用每一位来表示一个整数是否存在来节省空间，1表示存在，0表示不存在。

  

  • 位图优缺点
    （1）优点：位图所开空间只与范围有关，节省空间，在处理海量数据问题时，可使用位图；例如：在40亿个数中判断一个数是否存在
    （2）缺点：通过位图所得到的结果不精确

  • 位图操作
    （1）插入：注意位置的计算，先计算待插入元素在数组当中的位置，在计算在哪一个比特位
    （2）重置：和插入一样，找到位置，进行去反即可
    （3）查找：因为是1代表存在，故利用按位与（&）操作符查看是否为1

• 扩展二（布隆过滤器）

  • 概念
    Bloom Filter是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。

  • 特点
    （1）它适用于判断元素是否存在集合当中，速率非常高。Bloom Filter有可能会出现错误判断，但不会漏掉判断。
    （2）Bloom Filter可以准确的判断出某个元素不在集合之中。但如果判断某个元素存在集合中，有一定的概率判断错误。因此，Bloom Filter不适合那些“零错误”的应用场合。
    （3）在能容忍低错误率的应用场合下，Bloom Filter比其他查找算法（如hash，折半查找）极大节省了空间。

  • 结构
    （1）数组：既然是哈希的扩展，结构中必然包含数组，但此数组是有比特位（bite）组成的数组
    （2）含有多个哈希函数，为了表达S={x1, x2,…,xn}这样一个n个元素的集合，Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,n}的范围中。

  • 操作
    （1）插入：布隆的结构里有多个哈希函数，必然某一数据的关键码映射到数组的位置不止一个
    （2）删除：一个数据对应多个位置，故删除一个必然会影响其他数据，布隆过滤器的操作里不支持删除
    （3）查找：前面布隆的特点已经说过查找会出现误差，故布隆不适合出现在“零错误”的场合

  • 应用
    （1）对y使用k个哈希函数得到k个哈希值
    （2）判断是否所有hash(y)的位置都是1（1≤i≤k），即k个位置都被设置为1了，
    （3）如果所有位置都已置成了‘1’，y就可能集合中的元素；只有一个位置上是‘0’，那y一定不是集合中的元素。
    注意1：布隆过滤器无法准确判断某个元素存在于集合中，因为一个不存在元素通过k个哈希函数映射出来的位置上的值可能都是‘1’。
    注意2：布隆过滤器不能删除元素。删除一个元素就要把k个位置置为‘0’，这样就会影响其他元素。（可以改进）

  • 改进

      前面我们提到布隆过滤器不能删除元素这一缺点是可以改进的，解决方案是用多个bit来存储一个元素。这里为了计算方便，采用32bit来存储。全‘0’代表不存在，出现一个便加一，删除元素时把对应位置减一就可以了。

位图和布隆具体操作源码可点下面链接：
http://blog.csdn.net/zhangye3017/article/details/79477293

位图和布隆经典例题，可以点下面链接
http://blog.csdn.net/zhangye3017/article/details/79431449