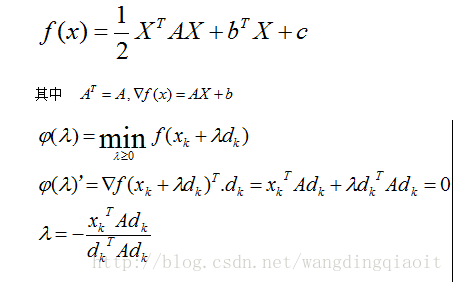最速梯度下降法及matlab实践
最速梯度下降法及matlab实践
写在前面
梯度下降法属于最优化理论与算法中的研究内容，本文介绍了利用MATLAB实现最速梯度下降法过程中的容易出错的几点，并附上实验代码和运行结果。为了保持简单，和避免重复劳动，关于梯度下降法的原理与算法步骤，本文不再赘述，你可以到我的资源免费下载本节的所有关于原理部分的资料。关于文中涉及到的重要函数，你可以到MATLAB文档帮助中心搜索。
本节要求掌握：梯度下降法的原理；基于matlab实现梯度下降法的原理与技巧
1.实现最速梯度下降法MATLAB关键几点
1)建立符号表达式表达函数
建立函数表达式可以使用matlab中的符号变量和符号表达式功能。
如下示例,利用三种方式构造函数表达式x^2+x-2,并将其转换为多项式，求其根。
%构成符号表达式方法一:
fx = sym('x^2+x-2');% 利用sym('符号字符串')构成符号表达式
ployx = sym2poly(fx)% 转换成多项式
roots(ployx);% 原符号表达式转换为多项式后求根
ans =
-2
1
%构成符号表达式方法二:
syms x;%利用syms定义符号变量
fx = x^2+x-2;%利用已定义的符号变量组成符号表达式
polyx = sym2poly(fx);
roots(polyx)
ans =
-2
1
%构成符号表达式方法三:
fx = 'x^2+x-2';%利用单引号建立符号表达式，与之前定义有区别，实质上定义的是char类型
fx = sym(fx);%转换为真正意义的符号表达式
polyx = sym2poly(fx);
roots(polyx)
ans =
-2
1注意两点:
a. 利用单引号生成的符号表达式建立的并不是真正意义上的符号表达式（sym类型），就是一个普通的字符串（char类型）。
如以下示例:
>> fx = 'x^2+x-2';
>> fy = sym('y^2+y-2');
>> whos
Name Size Bytes Class Attributes
fx 1x7 14 char
fy 1x1 60 sym 我们可以发现，利用单引号创建的符号表达式存贮为char类型，而不是sym类型。
因此使用单引号创建符号表达式时注意作用在其上函数的影响，要将其转换为真正符号表达式，如:
>> y = 'x^3+x^5'
y =
x^3+x^5
>> diff(y) %计算结果明显错误
ans =
-26 -43 -8 77 -26 -41
>> diff(sym(y)) %先转换为符号表达式，再求微分，结果正确
ans =
5*x^4 + 3*x^2b.符号表达式计算的结果必要时要转换为数值类型
例如，
>> syms x;
>> fx = x^2+x-2;
>> ret = solve(fx)
ret =
1
-2
>> whos ret
Name Size Bytes Class Attributes
ret 2x1 60 sym
>> ret = double(ret);%利用double函数将sym类型转换为数值类型
>> whos ret
Name Size Bytes Class Attributes
ret 2x1 16 double 这里利用solve函数返回的根，是符号变量，将它直接与数值类型计算时，将产生错误，利用double将其转换为数值类型。
2)求解函数的梯度，从而获取搜索方向
求解函数梯度需要利用gradient函数，代入某个位置，求具体点的梯度需要使用subs函数，示例如下:
>> syms x1 x2;
X = [x1;x2];
fx = x1-x2+2*x1^2+2*x1*x2+x2^2;
>> gradx = gradient(fx,X) %计算梯度函数
gradx =
4*x1 + 2*x2 + 1
2*x1 + 2*x2 - 1
>> ret = subs(gradx,X,[1 2]) %计算在点(1,2)处梯度
ret =
9
53)寻找最佳步长
最佳步长，需要求解方程: step* = min f(x[k]+step*d[k]),其中x[k]表示当前位置，step表示步长，d[k]表示当前搜索方向,step*表示所求去的理想步长。
理想步长的求解，就是求解使上述方程取最小值的步长，可以通过求导函数的实数零点来获取。
这个地方需要使用符号变量和符号表达式的技巧，具体可参见代码清单2-2部分的函数getNextStep(fx,var,xk,dk) 。
4)精度控制问题
一方面利用精度控制迭代的过程的终止，另一方面如果你想观察计算过程也要控制精度。
如果没有控制精度，很有可能把正确的计算结果当成错误的结果。例如：
>> ft = sym('(44*t-2)^4+(92*t-6)^2');
>> ft_diff = diff(ft);%求导数
>> roots = solve(ft_diff) %求导数方程的根
roots =
((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3) - 529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + 1/22
(3^(1/2)*(529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3))*i)/2 + 529/(2811072*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) - ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)/2 + 1/22
529/(2811072*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) - (3^(1/2)*(529/(1405536*((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)) + ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3))*i)/2 - ((493684489^(1/2)*2776680568306630656^(1/2))/2776680568306630656 + 115/10307264)^(1/3)/2 + 1/22
>> roots = vpa(solve(ft_diff)) %控制位默认精度显示
roots =
0.0615348488488
0.0374143937574 + 0.0363735994416*i
0.0374143937574 - 0.0363735994416*i
>> size(roots)
ans =
3 12.算例演示
算例部分例子，已经相关资料的算例比对过，求解过程是正确的。
1）正定二次函数的极小值点
这里通过求取典型的正定二次函数f(X)，设步长为lambda,则最佳步长计算过程如下(这是我的推导):
因此可以通过梯度和最佳步长编写计算正定二次型函数的梯度极小点求解函数如下:
function [ y ] = GDMin(A,b,x,e,MAX)
% 正定二次型函数的最速梯度下降法求解正定二次函数极小点
% A 表示主系数矩阵
% b 表示副系数矩阵
% x 表示起始点
% e 表示精度控制
% MAX 表示迭代次数控制
if nargin < 5
MAX = 10;%设置默认最大迭代次数
end
if A ~= A'
error('input matrix is not symmetrical ');%检查A是否为对称阵
end
%开始循环迭代
for k=1:1:MAX
direction = -(A*x+b);
disp('------------------------------');
fprintf('d[%d]=:',k);
disp(direction');
if normest(direction) <= e
y = x;
break;
else
fprintf('X[%d]=:',k);
disp(x');
step = -(x'*A+b')*direction/(direction'*A*direction);
fprintf('step(%d)=: ', k);
disp(step);
disp('------------------------------');
x = x+step*direction;
end
end
end
算例如下:
syms x1,x2;
X = [x1;x2];
fx = 2*x1^2+x2^2;
>> minVal =GDMin([4 0;0 2],[0;0],[1;1],0.1)
------------------------------
d[1]=: -4 -2
X[1]=: 1 1
step(1)=: 5/18
------------------------------
------------------------------
d[2]=: 4/9 -8/9
X[2]=: -1/9 4/9
step(2)=: 5/12
------------------------------
------------------------------
d[3]=: -8/27 -4/27
X[3]=: 2/27 2/27
step(3)=: 5/18
------------------------------
------------------------------
d[4]=: 8/243 -16/243
minVal =
-2/243
8/243 2)一般函数的极小值点
从正定二次型函数推广到一般函数，需要注意梯度函数的求法和最佳步长的确定，文中链接提供的资料中有关于原理部分的详细介绍，这里不再赘述。
设计的代码如下:
function [ y ] = GDMin2(fx,var,x,e,MAX)
% 最速梯度下降法求解函数极小点
% author : wandq
% time : 2014-4-10
% 参数描述------------------------------
% fx 符号表达式 如fx = (x1-2)^4+(x1-2*x2)^2；
% var 符号变量列表 如：syms x1 x2;var= [x1;x2];
% x 起始位置
% e 精度控制
% MAX 最大迭代次数控制
% ------------------------------
if nargin < 5
MAX = 10;%设置默认最大迭代次数
end
precision = 3;%显示精度控制
%开始循环迭代
%direction存贮搜索方向
%step 存贮步长
bfound = 0;
for k=1:1:MAX
direction = getNextDirecrion(fx,var,x);
disp('------------------------------');
fprintf('d[%d]=:',k);
disp( vpa(direction',precision) );
if normest(direction) <= e
y = x;
bfound = 1;%得到结果时置为1
break;
else
step = getNextStep(fx,var, x,direction);%计算步长
if isempty(step)
error('can not find a proper step.');
end
%打印求解过程
fprintf('X[%d]=:',k);
disp( vpa(x',precision) );
fprintf('step(%d)=: ', k);
disp( vpa(step,precision) );
disp('------------------------------');
x = x+step*direction;%计算下一个位置
end
end
if bfound == 1
disp('min value of:');
disp( vpa( subs(fx,var,y),precision) );
end
end
%根据位置xk,获取搜索方向
function [direction] = getNextDirecrion(fx,var,xk)
gx = gradient(fx,var); %计算梯度函数
direction = -subs(gx,var,xk);%计算搜索方向
end
%根据位置xk和方向dk,获取搜索步长step
%注意符号表达式求导数的根时返回值转换为double类型
function [step] =getNextStep(fx,var,xk,dk)
syms lambda;
phix = subs(fx,var,xk+lambda*dk);
phix_diff = diff(phix);
step = double(solve(phix_diff,'Real',true));%求取导函数的实数根
end算例如下:
>> syms x1 x2;
X = [x1;x2];
fx = (x1-2)^4+(x1-2*x2)^2;
x1 = [0;3];
e = 0.1;
>> minVal = GDMin2(fx,X,x1,e)
------------------------------
d[1]=:[ 44.0, -24.0]
X[1]=:[ 0, 3.0]
step(1)=: 0.0615
------------------------------
------------------------------
d[2]=:[ -0.739, -1.36]
X[2]=:[ 2.71, 1.52]
step(2)=: 0.231
------------------------------
------------------------------
d[3]=:[ -0.851, 0.464]
X[3]=:[ 2.54, 1.21]
step(3)=: 0.112
------------------------------
------------------------------
d[4]=:[ -0.18, -0.33]
X[4]=:[ 2.44, 1.26]
step(4)=: 0.267
------------------------------
------------------------------
d[5]=:[ -0.336, 0.183]
X[5]=:[ 2.39, 1.17]
step(5)=: 0.125
------------------------------
------------------------------
d[6]=:[ -0.091, -0.167]
X[6]=:[ 2.35, 1.2]
step(6)=: 0.279
------------------------------
------------------------------
d[7]=:[ -0.191, 0.104]
X[7]=:[ 2.33, 1.15]
step(7)=: 0.131
------------------------------
------------------------------
d[8]=:[ -0.0572, -0.105]
X[8]=:[ 2.3, 1.16]
step(8)=: 0.286
------------------------------
------------------------------
d[9]=:[ -0.128, 0.0696]
X[9]=:[ 2.29, 1.13]
step(9)=: 0.134
------------------------------
------------------------------
d[10]=:[ -0.0402, -0.0737]
min value of:
0.0055
minVal =
1227/541
902/789
这里提供几个算例，可以自行求解并与提供的资料中的数据比对：
算例1
syms x1 x2;
X = [x1;x2];
fx = x1-x2+2*x1^2+2*x1*x2+x2^2;
x1 = [0;0]
e = 0.1;
算例2
syms x1 x2;
X = [x1;x2];
fx = (3*x1^2)/2+(x2^2)/2-x1*x2-2*x1;
x1 = [0;0];
e = 0.01;
算例1
syms x1 x2;
X = [x1;x2];
fx = x1-x2+2*x1^2+2*x1*x2+x2^2;
x1 = [0;0]
e = 0.1;
算例2
syms x1 x2;
X = [x1;x2];
fx = (3*x1^2)/2+(x2^2)/2-x1*x2-2*x1;
x1 = [0;0];
e = 0.01;
另外，关于共轭梯度下降法也有相应的原理和算法，这里不做介绍，有兴趣的可查阅相关资料并根据文中提供的方法，自行练习。