吴恩达机器学习第五次作业(python 实现):偏差与方差
偏差与方差
import numpy as np
import matplotlib.pyplot as plt
import time
from scipy.io import loadmat
import scipy.optimize as opt
def loadfile(path):
data=loadmat(path)
return data
def draw_data(x,y):
plt.scatter(x,y)
plt.xlabel('water lever')
plt.ylabel('amount of water flowing out')
plt.title('Raw data')
return plt
def random_theta(row,col):
return np.array([np.random.uniform(0,1,row*col)]).reshape(row,col)
# 正则化代价函数
def reg_cost(theta,x,y,lam):
m=x.shape[0]
first=np.sum(np.power((x.dot(theta)-y),2))/(2*m)
second=lam*(theta[1:].dot(theta[1:]))/(2*m)
j=first+second
return j
# 梯度下降法
def gradient(theta,x,y,lam):
alpha=0.001
epoch=4000
cost=[]
m=x.shape[0]
for i in range(epoch):
partial=partial_gradient(theta,x,y,lam)
theta=theta-alpha*partial
cost.append(reg_cost(theta,x,y,lam))
return theta,cost
# 求代价函数j的偏导数
def partial_gradient(theta,x,y,lam):
m=x.shape[0]
first = ((x.dot(theta) - y).T.dot(x)) / m
second = lam * theta / m
second[0] = 0
partial = first + second
return partial
# 高级优化方法学习theta
def learn_theta(x,y,lam):
theta=np.ones(x.shape[1])
result=opt.minimize(fun=reg_cost,x0=theta,args=(x,y,lam),method='tnc',jac=partial_gradient)
return result.x
# 绘制迭代次数与代价j的关系
def draw_cost(cost):
x=np.arange(0,4000)
plt.plot(x,cost)
plt.title('iteration and cost')
plt.xlabel('iteration')
plt.ylabel('cost')
plt.show()
# 绘制回归曲线
def draw_linear(theta,x,x1,y1):
y=x@theta
plt=draw_data(x1,y1)
plt.plot(x[:,1],y)
plt.title('regression line')
plt.xlabel('water lever')
plt.ylabel('amount of water flowing out')
plt.show()
# 绘制多项式回归曲线
def draw_poly_linear(theta,x1,y1,means,std):
plt = draw_data(x1, y1)
# 将矩阵分成50份,实现曲线平滑
xnew=np.array(np.linspace(-60,60,60))
x2=np.c_[np.ones(len(xnew)),xnew]
xp=poly_feature(x2,6)
x=feature_normal(xp,means,std) # 这里要用训练集的平均值和标准差
y=x@theta
plt.plot(xp[:,1],y)
plt.title('poly regression line')
plt.xlabel('water lever')
plt.ylabel('amount of water flowing out')
plt.show()
# 绘制学习曲线
def learning_curves(x,y,xcv,ycv,lam):
x1=range(1,x.shape[0]+1)
cost_cv=[]
cost_train=[]
for i in range(1,x.shape[0]+1):
# 每次对m取不同的值,都学习一次theta
theta1=learn_theta(x[:i],y[:i],lam)
cost_train.append(reg_cost(theta1,x[:i],y[:i],0))
# 用整个cv集去测试
cost_cv.append(reg_cost(theta1,xcv,ycv,0))
plt.figure(figsize=(8,8))
plt.plot(x1,cost_cv,c='r',label="cv")
plt.plot(x1,cost_train,c='g',label="train")
plt.title('learning curves')
plt.xlabel('number of m')
plt.ylabel('error')
plt.grid(True)
plt.legend()
plt.show()
# 添加特征多项式
def poly_feature(x,power):
xp=x.copy()
for i in range(2,power+1):
xp=np.c_[xp,np.power(xp[:,1],i)]
return xp
# 特征归一化
def feature_normal(x,means,std):
xn=x.copy()
xn=(xn[:,1:]-means[1:])/std[1:]
return np.c_[np.ones(xn.shape[0]),xn]
# 获得均值与方差
def get_mean_std(x):
means = np.mean(x, axis=0)
std = np.std(x, axis=0, ddof=1) # 无偏标准差
return means,std
# lam-error曲线确定lam
def lam_error(xn,y,xcvn,ycv):
lams=[0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
error_cv=[]
error_train=[]
for l in lams:
theta=learn_theta(xn,y,l)
error_train.append(reg_cost(theta,xn,y,0))
error_cv.append(reg_cost(theta,xcvn,ycv,0))
plt.plot(lams,error_train,label='train')
plt.plot(lams,error_cv,label='cv')
plt.legend()
plt.grid(True)
plt.title('lam-error')
plt.xlabel('lambda')
plt.ylabel('error')
plt.show()
print('lambda should be',lams[np.argmin(error_cv)]) # lambda should be 3
def main():
start=time.process_time()
rawdata=loadfile('venv/lib/dataset/ex5data1.mat')
# training set
x1=rawdata['X'].ravel()
y=rawdata['y'].ravel()
x=np.c_[np.ones(x1.shape[0]),x1]
# cross validation set
xcv1=rawdata['Xval']
ycv=rawdata['yval'].ravel()
xcv=np.c_[np.ones(xcv1.shape[0]),xcv1]
# test set
xtest1=rawdata['Xtest']
ytest=rawdata['ytest'].ravel()
xtest=np.c_[np.ones(xtest1.shape[0]),xtest1]
# init theta
theta=np.ones(x.shape[1])
p=draw_data(x1,y)
p.show()
# print(reg_cost(theta,x,y,0)) # 303.9515255535976
# theta,cost=gradient(theta,x,y,1) # 梯度下降法
theta=learn_theta(x,y,0) # 高级优化法
# print(reg_cost(theta,x,y,0)) # 22.373906495108923
draw_linear(theta,x,x1,y) # 绘制拟合曲线
# draw_cost(cost)
# learning_curves(x,y,xcv,ycv,0) # 欠拟合
# 多项式回归
xp=poly_feature(x,6)
means,std=get_mean_std(xp)
xn=feature_normal(xp,means,std)
# 先将lambda设为0,然后在慢慢调整
theta=learn_theta(xn,y,0)
# print(reg_cost(theta, xn, y, 0)) # 0.19805305183075475
# draw_poly_linear(theta,x1,y,means,std) #平滑曲线
xcvp = poly_feature(xcv, 6)
xcvn = feature_normal(xcvp,means,std)
# learning_curves(xn,y,xcvn,ycv,0) # 过拟合
# lam_error(xn,y,xcvn,ycv)
end=time.process_time()
print("run time is",(end-start),'s.')
main()
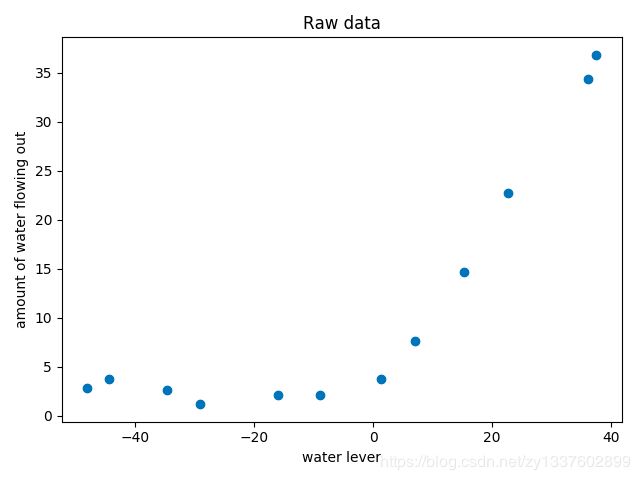
初始数据:
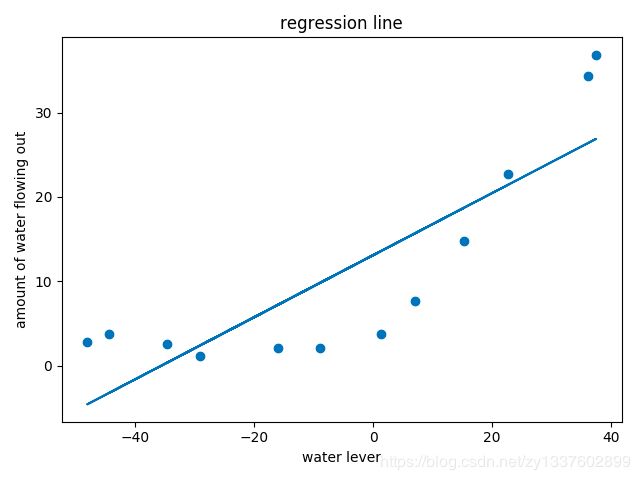
回归:很明显这个模型不合适(先将lambda的值设为1,后面在调整)
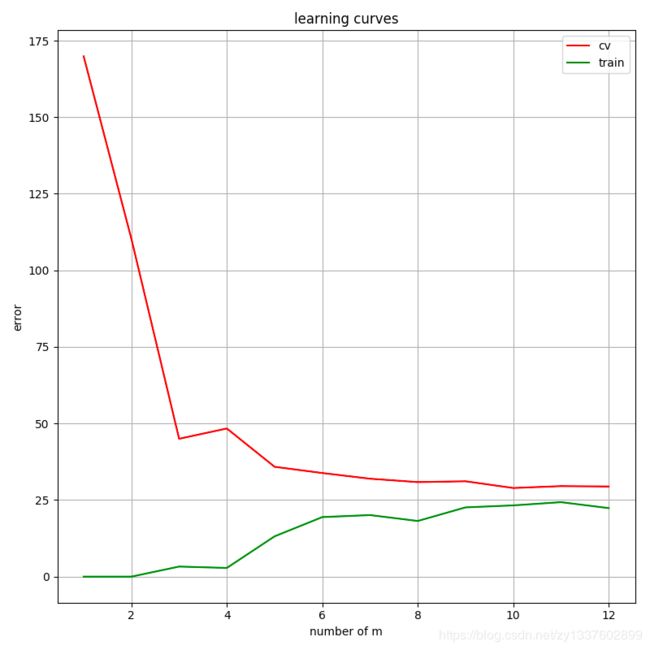
接着绘制学习曲线:通过不断的增加样本数量来训练,绘制出 J c v J_{cv} Jcv与 J t r a i n J_{train} Jtrain
需要注意的是:对于每次训练样本数量不同时,都要做一次训练,然后用相应的训练样本去计算 J t r a i n J_{train} Jtrain,并且用所有交叉验证集去计算 J c v J_{cv} Jcv
# 绘制学习曲线
def learning_curves(x,y,xcv,ycv,lam):
x1=range(1,x.shape[0]+1)
cost_cv=[]
cost_train=[]
for i in range(1,x.shape[0]+1):
# 每次对m取不同的值,都学习一次theta
theta1=learn_theta(x[:i],y[:i],lam)
cost_train.append(reg_cost(theta1,x[:i],y[:i],0))
# 用整个cv集去测试
cost_cv.append(reg_cost(theta1,xcv,ycv,0))
plt.figure(figsize=(8,8))
plt.plot(x1,cost_cv,c='r',label="cv")
plt.plot(x1,cost_train,c='g',label="train")
plt.title('learning curves')
plt.xlabel('number of m')
plt.ylabel('error')
plt.grid(True)
plt.legend()
plt.show()
可以看出,这种情况属于高偏差,下一步我们要进行特征映射获取特征多项式来,通过增加特征数来降低偏差
特征映射(获取特征多项式):
首先进行特征映射获取特征多项式: 1 , x , x 2 , x 3 , ⋅ ⋅ ⋅ , x n 1,x,x^{2},x^{3},···,x^{n} 1,x,x2,x3,⋅⋅⋅,xn
# 添加特征多项式
def poly_feature(x,power):
xp=x.copy()
for i in range(2,power+1):
xp=np.c_[xp,np.power(xp[:,1],i)]
return xp
通常特征映射完后,要做特征归一化
归一化的时候我们要用到均值与方差 x i = x i − m e a n s t d x_{i}=\frac{x_{i}-mean}{std} xi=stdxi−mean(或者 x i = x i − m e a n m a x − m i n x_{i}=\frac{x_{i}-mean}{max-min} xi=max−minxi−mean也可以)
首先获取均值与方差
# 获得均值与方差
def get_mean_std(x):
means = np.mean(x, axis=0)
std = np.std(x, axis=0, ddof=1) # 无偏标准差
return means,std
然后进行特征归一化,第一列全为1,不用归一化
# 特征归一化
def feature_normal(x,means,std):
xn=x.copy()
xn=(xn[:,1:]-means[1:])/std[1:]
return np.c_[np.ones(xn.shape[0]),xn]
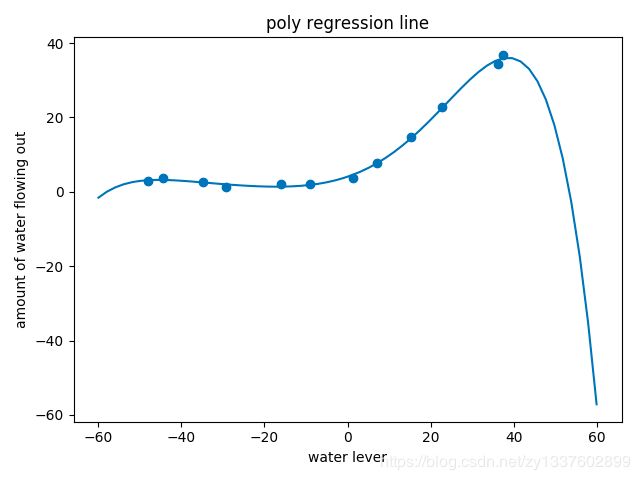
然后就是绘制多项式回归曲线,这里需要注意的是:为了让曲线平滑,我们定义xnew集,对xnew集特征映射和归一化的时候,不要用xnew集对means和std,要用训练集的means和std
# 绘制多项式回归曲线
def draw_poly_linear(theta,x1,y1,means,std):
plt = draw_data(x1, y1)
# 将矩阵分成50份,实现曲线平滑
xnew=np.array(np.linspace(-60,60,60))
x2=np.c_[np.ones(len(xnew)),xnew]
xp=poly_feature(x2,6)
x=feature_normal(xp,means,std) # 这里要用训练集的平均值和标准差
y=x@theta
plt.plot(xp[:,1],y)
plt.title('poly regression line')
plt.xlabel('water lever')
plt.ylabel('amount of water flowing out')
plt.show()
绘制出多项式回归曲线:
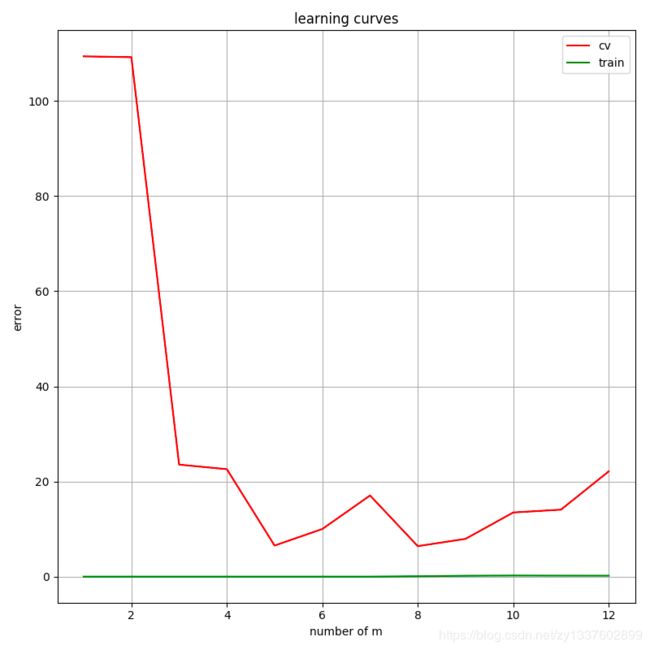
然后绘制学习曲线,此时可以看出欠拟合
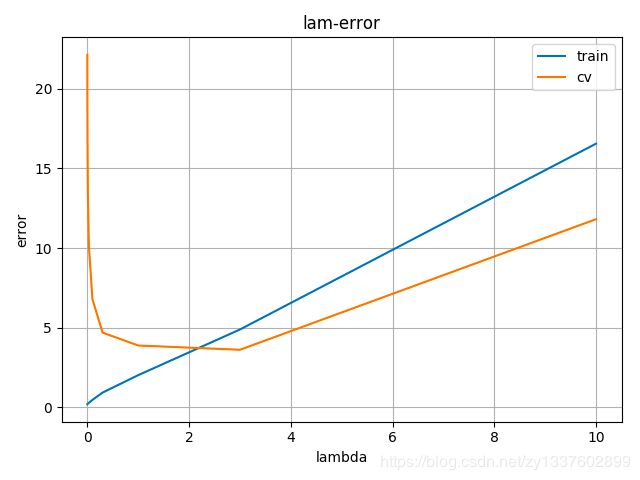
此时我们通过修改lambda的值来调整,设置lambda从[0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]选择, J c v J_{cv} Jcv最小值对应的lambda即合适的lambda
# lam-error曲线确定lam
def lam_error(xn,y,xcvn,ycv):
lams=[0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
error_cv=[]
error_train=[]
for l in lams:
theta=learn_theta(xn,y,l)
error_train.append(reg_cost(theta,xn,y,0))
error_cv.append(reg_cost(theta,xcvn,ycv,0))
plt.plot(lams,error_train,label='train')
plt.plot(lams,error_cv,label='cv')
plt.legend()
plt.grid(True)
plt.title('lam-error')
plt.xlabel('lambda')
plt.ylabel('error')
plt.show()
print('lambda should be',lams[np.argmin(error_cv)]) # lambda should be 3
lambda should be 3
设置lam=3
theta=learn_theta(xn,y,3)