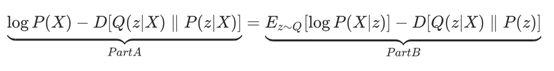使用PyTorch从理论到实践理解变分自编码器VAE
变分自动编码器(Variational Auto Encoders,VAE)是种隐藏变量模型[1,2]。该模型的思想在于:由模型所生成的数据可以经变量参数化,而这些变量将生成具有给定数据的特征。因此,这些变量被称为隐藏变量。
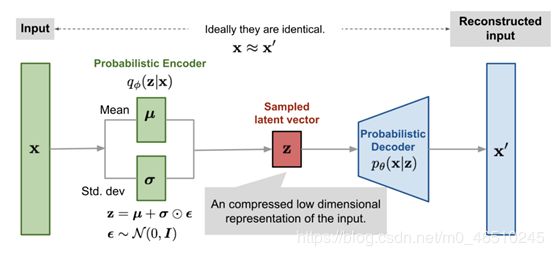
而VAE背后的关键点在于:为了从样本空间中找到能够生成合适输出的样本(就是能输出尽可能接近我们所规定分布的数据),它并没有试图去直接构造一个隐藏空间(隐藏变量所在的空间),而是构造了一个类似于具有编码器和解码器两个部分的网络:
编码器部分能够学习到根据输入样本X来形成一个特定分布,从中我们可以对一个隐藏变量进行采样,而这个隐藏变量极有可能生成X里面的样本。换句话说,可以理解为编码器通过学习一组参数θ1来得到一个能计算出Q(X,θ1)分布样本的模型,通过抽样能够使得隐藏变量z的P(X|z)最大化。
而解码器部分能够学习到根据给定的一个隐藏变量z作为输入,生成一个具有真实数据分布的输出。换句话说,可以理解为解码器通过学习一组参数θ2来得到一个能映射到隐藏空间分布的函数f(z,θ2),从而能够输出与真实数据具有相同分布的数据集。
为了充分理解VAE背后的数学意义,我们将通过对其理论讲解以及与一些传统方法进行比较来说明。
这篇文章将包含以下内容
如何对隐藏空间进行定义?
如何高效的从隐藏空间中生成数据?
VAE最终的框架是什么?
通过一些实验来展示VAE中的一些有趣特征。
潜在变量模型
隐藏变量模型这一说法是根据:模型所生成的数据是通过对隐藏变量进行参数化而来。而这个名称具有这样一个事实:对于能够生成我们所需数据的模型,我们并不需要知道这个模型在哪设置了隐藏变量。
在一些测试场合,对于一个在高维空间Z中的隐藏向量z,我们能够很轻松的根据它的概率密度函数P(z)进行抽样。这时,我们能够得到一些较为确定的函数f(z;θ),其中θ能够被参数化到Θ空间,具体表示为:f
:Z×Θ→X。式中f是一个确定的映射关系,当z具有随机性而θ是一个固定参数时,f(z;θ)
就是X张成空间中的随机变量。
在训练过程中,我们通过优化参数θ来使得根据P(z)抽取出的z具有更高的概率,从而通过f(z;θ)函数得到的数据能更加接近真实样本X中的数据。总之为了实现这一目的,我们需要去找到这样的参数θ:
在上式中,为了使得X与z的关系更加直观,我们使用了总体概率密度进行计算,即采用P(X|z;θ)分布来替换f(z;θ)分布。此外,我们还做了另外一个假设:P(W|z;θ)遵循N(X|f(z;
θ),σ*I)类型的高斯分布。(这样做的目的是:可以认为生成的数据几乎是X中的数据,但却又不完全是X中的数据)
定义隐藏空间
正如开始介绍的那样,隐藏空间是一个假设的模型,该空间中的一些变量能够影响到我们数据分布中的一些特定的特征。我们可以想象下,如果我们的数据假设为是由汽车组成的以及数据的分布类比于汽车的空间,那么这个隐藏变量可以理解为影响汽车颜色、每个部件的位置以及车门的数量的因素。
然而,直接去明确每个隐藏变量是非常困难的,特别是当我们所需处理的数据具有上百个维度时。并且当其中一个隐藏变量与另一个隐藏变量存在一定耦合关系时,人工去定义这些隐藏变量将变得更加困难,换句话说就是对于P(z)的复杂分布很难通过人工去进行定义。
解决方案
为了解决这一问题,我们以反向传播的方式,采用数学中概率分布的性质和神经网络的能力来学习出这些样本所服从的函数。
使得该问题能被更容易处理的数学性质:对于一个d维的任意分布,它都能够通过选取一组d个服从正态分布的变量并将它们映射到一个足够复杂的函数中来生成。因此,我们可以假定我们的隐藏变量服从高斯分布,然后构造出一个具体的函数将我们服从高斯分布的隐藏空间映射到一个更为复杂的分布当中,这样我们就能通过取样来生成我们需要的数据了。其中,这个具体的函数需要把简单的隐藏分布映射成一个更为复杂的分布,而这样的一个复杂分布可以看作是一个隐藏空间,这时就可以采用神经网络来建立出一些参数,因此这些参数就能够在训练中进行微调了。
学会从潜在空间中生成数据
在进入本文最有趣的部分之前,让我们先回顾一下最终的目标:我们有一个服从正态分布的d维隐藏空间,以及我们所要学习的f(z;θ2)函数能够将隐藏分布映射到真实数据的分布。换句话说就是:我们先对隐藏变量进行采样,然后将这个隐藏变量作为生成器的输入,最后生成的数据样本能够尽可能的接近真实的数据。
我们需要解决以下两件事情
1.为了使得变量z的概率密度P(X|z)最大化,如何高效的对隐藏空间进行探索?(我们需要在训练过程中为给定的X找到最为正确的z)
2.如何使用反向传播来训练这整个过程?(我们需要找到一个具体对象来优化f:P(z)映射到P(X))
为我们的X找到正确的隐藏变量z
在绝大多数的实验中,z和P(X|z)的数值都接近于零,因此我们对P(X)的估计几乎没有什么意义。而VAE的核心思想在于:需要尝试对可能产生X的z值进行不断采样,然后从这些值中计算出P(X)的大小。为了做到这一点,我们首先需要构建一个能够给出X的值并给出可能产生z的值的X分布的这样一个新函数Q(z|X),并希望在Q函数下的z值的空间大小比P(z)下的z值的空间大小要小得多。
对于VAE的编码器与所假定出的Q函数,我们采用神经网络来对其进行训练,使得输入X能映射到输出Q(z|X)的分布中,从而帮助我们能够找到一个最好的z来生成实际X中的数据。
使用反向传播训练模型
为了更好理解到我们的VAE是如何训练出来的,首先我们需要定义一个明确的目标,而为了做到这一点,我们又需要做一些数学公式的推导。
让我们从编码器开始说起,我们是想让Q(z|X)的分布无限接近于P(X|z)的分布,为了确定出这两个分布到底有多接近,我们可以采用两个分布间的Kullback-Leibler散度D来进行度量:
通过数学推导,我们可以把这个等式写成更为有趣的形式。对P(z|X)使用贝叶斯定律后,等式如下:
还可以表示成如下等式:
花点时间看看这个公式
对于A部分:就是在等式左边的这一项,它对于反向传播来说并不是一个有利的设定(我们并不知道P
(X)的表达式是多少),但是我们可以知道如果想要在给定z的情况下最大化log(P(X)),可以通过最小化减号右边的部分来实现(这样可以使得Q(z|x)的分布尽可能接近P(z|X)的分布),这也正是我们在一开始时提到的最终目标。
对于B部分:等式右边的这一项就更加有趣,正如我们了解P(X|z)(这是解码器部分->生成器)和Q(z|X)(这是我们的编码器)。所以我们可以得出,为了最大化这一项,我们需要最大化log(P(X|z)),而这也就意味着我们不需要最大化log函数的极大似然概率和最小化Q(z|X)和P(z)之间的KL散度。
为了使得B部分更容易被计算,我们假设Q(z|X)是服从N(z|mu(X,θ1)或sigma(X,θ1))的高斯分布,其中θ1是在神经网络中需要从数据集中所学到的参数。此外,在我们的公式中还有一个问题还没被解决:就是如何计算反向传播中的期望(损失函数)?
损失函数部分的操作
一种思路是采用多次前向传递的方式来计算出log(P(X|z))的期望,但是其计算效率较低。从而我们希望通过随机训练来解决这一问题,首先我们假定在第n轮迭代中使用的数据Xi能代表整个数据集,因此可以考虑我们从样本Xi中所获得的log(P(Xi|zi))和代表log(P(X|z))对Q分布的期望zi。最后,这个解码器只是一个简单的生成器模型,而我们希望去重建这个输入图像,因此一个简单的方法是使用输入图像和生成图像之间的均方误差来作为其期望部分(损失函数),如下式。
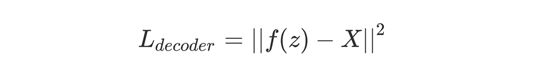
VAE的最终框架
正如在一开始所介绍的那样,我们知道VAE的最终结构由两个部分的网络所构成:
1.编码器部分能够学习到根据输入样本X来形成一个特定分布,从中我们可以对一个隐藏变量进行采样,而这个隐藏变量极有可能生成X里面的样本。为了使得Q(z|X)服从高斯分布,这部分需要被优化。
2.解码器部分能够学习到根据给定的一个隐藏变量z作为输入,生成一个具有真实数据分布的输出。该部分将经过采样后的z(最初来自正态分布)映射到一个更复杂的隐藏空间去(实际数据的空间),并通过这个复杂的隐藏变量z生成一个个的数据点,这些数据点十分接近我们真实数据的分布。
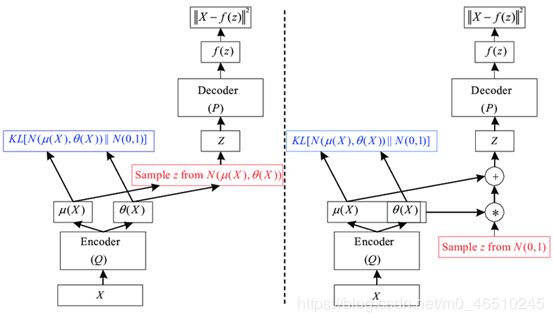
VAE的详细架构。左边的图和右边的图是类似的,只是左边示例中展示了反向传播,实际使用图一般为右边的示例
VAE实验分析
现在你已经了解到了VAE背后的数学理论,那么现在让我们看看通过VAE我们能够生成哪些模型,实验平台为PyTorch。
PyTorch的全局架构
class VAE(nn.Module):
def __init__(self, latent_dim):
super().__init__()
self.encoder = nn.Sequential(nn.Linear(28 * 28, 256),
nn.ReLU(),
nn.Linear(256, 128))
self.mu = nn.Linear(128, latent_dim)
self.logvar = nn.Linear(128, latent_dim)
self.latent_mapping = nn.Linear(latent_dim, 128)
self.decoder = nn.Sequential(nn.Linear(128, 256),
nn.ReLU(),
nn.Linear(256, 28 * 28))
def encode(self, x):
x = x.view(x.size(0), -1)
encoder = self.encoder(x)
mu, logvar = self.mu(encoder), self.logvar(encoder)
return mu, logvar
def sample_z(self, mu, logvar):
eps = torch.rand_like(mu)
return mu + eps * torch.exp(0.5 * logvar)
def decode(self, z,x):
latent_z = self.latent_mapping(z)
out = self.decoder(latent_z)
reshaped_out = torch.sigmoid(out).view(x.shape[0],1, 28,28)
return reshaped_out
def forward(self, x):
mu, logvar = self.encode(x)
z = self.sample_z(mu, logvar)
output = self.decode(z,x)
return output
训练模型
下图展示了我们在训练期过程中所得到的结果。为了演示,VAE已经在MNIST数据集[3]上经过了训练,每10轮展示一次,我们绘制了输入X和所生成的数据,而这些输出的数据又作为VAE的输入。
训练样本(输入在上,输出在下)------第1轮
训练样本(输入在上,输出在下)------第20轮
训练样本(输入在上,输出在下)------第30轮
训练样本(输入在上,输出在下)------第40轮
隐藏空间
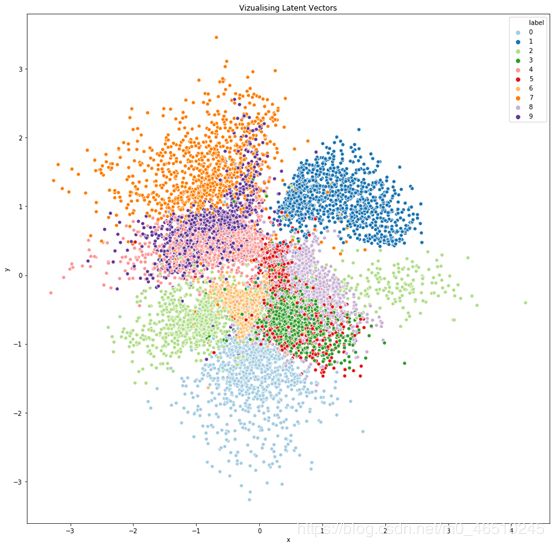
其中关于VAE有一个有趣的事情:在训练中学习到的隐藏空间有很好的连续性。为了能够在二维空间中轻松地可视化我们的数据点,我们考虑通过二维可视化隐藏空间的特性来实现。
在训练过程中,我们能够发现在2维隐藏空间中MNIST数据集被重新划分了,从中我们可以看到相似的数字被分在了一起(绿色的表示3且都被分在了一起,并且非常靠近数字8,说明这两个数字非常相似)。
2维图中可视化隐藏空间
一个更好地从视觉上去理解隐藏空间连续性的方法是:去观察从隐藏空间中所生成的图像。我们从下图中可看出,数字在隐藏空间内进行移动时被平滑地转换为了与之相似的数字。
二维隐藏空间中抽样出的数字
结论
VAE是一个令人惊叹的工具,它依靠神经网络的帮助能够解决一些具有挑战性的问题:生成模型。与传统方法相比,VAEs解决了两个主要的问题:
1.
如何在隐藏空间中抽取最相关的隐藏变量来给到输出。2.如何将隐藏空间中的数据分布映射到真实的数据分布中去。但是,VAE也存在着一些缺点:由于使用的是均方根误差,它使得生成器是收敛到了平均最优,导致生成的图像有一点模糊。
而生成对抗网络(GANs)通过使用鉴别器而不是均方根误差作为损失能解决这一问题,从而使得生成的图像更为真实。但是,由于GAN的隐藏空间难以控制,使得它不具有像VAEs那样的连续性,但这在某些应用场合中却是必要的。
参考文献:
[1] Doersch, C., 2016. Tutorial on variational autoencoders. arXiv
preprint arXiv:1606.05908.
[2] Kingma, D.P. and Welling, M., 2019. An introduction to variational
autoencoders. arXiv preprint arXiv:1906.02691.
[3] MNIST dataset, http://yann.lecun.com/exdb/mnist/
作者: Emrick Sinitambirivoutin
Deephub翻译组:李爱(Li Ai)