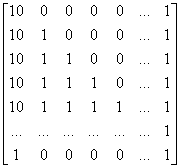ooooooooe
ooooooooe

HDU 5015 233 Matrix 矩阵快速幂

链接：http://acm.hdu.edu.cn/showproblem.php?pid=5015

题意：给一个n*m的矩阵(n ≤ 10,m ≤ 109)，给出矩阵中的A10,A20,A30...，矩阵中的A01=233,A02=2333,A03=23333...对于Aij来说，Aij=Ai-1j+Aij-1，问矩阵中的Anm是多少。

思路：行数只有10，所以可以进行逐列的递推，进行109的递推需要用矩阵快速幂。

递推矩阵：                                                          初始矩阵：

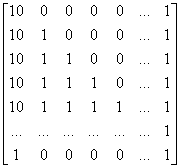
HDU 5015 233 Matrix 矩阵快速幂_第1张图片                               

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define eps 1e-8
#define INF 0x7fffffff
#define maxn 10005
#define PI acos(-1.0)
#define seed 31//131,1313
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
#define MOD 10000007
#define maxn 15
#define maxm 15
struct Matrix
{
    int n,m;
    LL a[maxn][maxm];
    void init()
    {
        n=m=0;
        memset(a,0,sizeof(a));
    }
    void change(int c,int d)
    {
        n=c;
        m=d;
    }
    Matrix operator +(const Matrix &b) const
    {
        Matrix tmp;
        tmp.n=n;
        tmp.m=m;
        for(int i=0; i>=1;
        m.Copy(m*m);
    }
    return tmp;
}
int main()
{
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
#endif
    Matrix A,B;
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        A.init();
        B.init();
        A.n=n+2;
        A.m=n+2;
        A.a[0][0]=10;
        A.a[0][n+1]=1;
        for(int i=1; i<=n; i++)
        {
            A.a[i][0]=10;
            for(int j=1; j<=i; j++)
                A.a[i][j]=1;
            A.a[i][n+1]=1;
        }
        A.a[n+1][n+1]=1;
        A=M_quick_pow(A,m);
        B.n=n+2;
        B.m=1;
        B.a[0][0]=23;
        for(int i=1; i<=n; i++)
        {
            scanf("%I64d",&B.a[i][0]);
            B.a[i][0]%=MOD;
        }
        B.a[n+1][0]=3;
        B.Copy(A*B);
        if(n==0&&m==0)
        {
            puts("0");
            continue;
        }
        printf("%I64d\n",B.a[n][0]);
    }
    return 0;
}


你可能感兴趣的:(数论,*矩阵)

  • 推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
    importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
  • matlab delsat = setdiff(1:69,unique(Eph(30,:)))； 语句含义 黄卷青灯77 matlab开发语言setdiff
    这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下：delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量，包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
  • 高级UI<第二十四篇>：Android中用到的矩阵常识 NoBugException
    （1）定义在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。由m×n个数aij排成的m行n列的数表称为m行n列的矩阵，简称m×n矩阵。记作：图片.png这m×n个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n，m×n矩阵A也记作Amn。元素是实数的矩阵称为实矩阵，元素是复
  • 【机器人建模和控制】读书笔记 Piccab0o 机器人
    机器人建模和控制——马克·斯庞A.x10=x1∙x0x^0_1=x_1\bulletx_0x10=x1∙x0，其实就是：1）x1x_1x1轴向量在O0O_0O0系下的坐标2）在x0x_0x0轴上的投影3）坐标变换矩阵的R10R_1^0R10的第一个元素B.点p在o1x1y1z1o_1x_1y_1z_1o1x1y1z1系下的坐标p1p^1p1可以表示为：p=ux1+vy1+wz1p=ux_1+vy_
  • 致良知之寄诸用明书 BonSun
    众所周知，当今社会，父母和社会、学校对学生的期望往往是唯分数论，包括每个人对成功的理解也往往是功名利禄，忽视了最基本的学问。文中提到，花之千叶者无实，为其华美太发露耳。人只有沉下心来，韬光养晦，才能拥有真正的学问和本领。
  • python 读写csv文件方法 菩提本无树007 pythonpandas开发语言
    csv是一种结构化文件，可以将文本转化成矩阵的形式，方便程序读取和处理。下面来介绍一下使用python读写csv文件的方法：1.首先需要使用pip安装python包，然后将csv文件解压到一个文件夹下2.使用pip安装python包，安装完成后在终端输入：3.在终端输入命令：4.输入完成后，打开终端，在命令行输入以下代码：5.最后输出结果，可以看到csv文件已经打开了。6.将csv文件放入到pyt
  • MATLAB语言基础教程、 小项目1：简单的计算器、 小项目2：有页面的计算器、使用App Designer创建GUI计算器 azuredragonz 学习教程matlab开发语言
    MATLABMATLAB语言基础教程1.MATLAB简介2.基本语法变量与赋值向量与矩阵矩阵运算数学函数控制流3.函数4.绘图案例：简单方程求解小项目1：简单的科学计算器功能代码项目说明小项目2：有页面的计算器使用AppDesigner创建GUI计算器主要步骤：完整代码（使用MATLAB编写）说明：如何运行：小项目总结MATLAB语言基础教程1.MATLAB简介MATLAB（矩阵实验室）是一种用于
  • np.identity()/np.eye() 听风1996
    两个函数的原型为：np.identity(n,dtype=None)np.eye(N,M=None,k=0,dtype=)；np.identity只能创建方形矩阵np.eye可以创建矩形矩阵，且k值可以调节，为1的对角线的位置偏离度，0居中，1向上偏离1，2偏离2，以此类推，-1向下偏离。值绝对值过大就偏离出去了，整个矩阵就全是0了。两者在创建单位矩阵上，并无区别，两者的区别主要在接口上；np.i
  • 图像匹配---（Python） 阳光下的Smiles Python图像处理
    图像匹配---（Python）图像匹配分为以灰度为基础的匹配和以特征为基础的匹配：（1）灰度匹配是基于像素的匹配。灰度匹配通过利用某种相似性度量，如相关函数、协方差函数、差平方和、差绝对值和等测度极值，判定两幅图像中的对应关系。（2）特征匹配则是基于区域的匹配。基于特征的匹配所处理的图像一般包含的特征有颜色特征、纹理特征、形状特征、空间位置特征等1、差分矩阵求和差分矩阵=图像A矩阵数据-图像B矩阵
  • 洛谷P1719 最大加权矩形 0hang 算法c++开发语言
    洛谷P1719最大加权矩形题目描述为了更好的备战NOIP2013，电脑组的几个女孩子LYQ,ZSC,ZHQ认为，我们不光需要机房，我们还需要运动，于是就决定找校长申请一块电脑组的课余运动场地，听说她们都是电脑组的高手，校长没有马上答应他们，而是先给她们出了一道数学题，并且告诉她们：你们能获得的运动场地的面积就是你们能找到的这个最大的数字。校长先给他们一个n\timesnn×n矩阵。要求矩阵中最大加
  • 4×4矩阵键盘详解（STM32） 辰哥单片机设计 STM32传感器教学矩阵计算机外设stm32嵌入式硬件单片机传感器
    目录一、介绍二、传感器原理1.原理图2.工作原理介绍三、程序设计main.c文件button4_4.h文件button4_4.c文件四、实验效果五、资料获取项目分享一、介绍矩阵键盘，又称为行列式键盘，是用4条I/O线作为行线，4条I/O线作为列线组成的键盘。在行线和列线的每一个交叉点上设置一个按键，因此键盘中按键的个数是4×4个。这种行列式键盘结构能够有效地提高单片机系统中I/O口的利用率，节约单
  • 抖音开始怎么吸粉（可以试试这几种办法） 配音新手圈
    如何在抖音短视频平台上快速积累人气和粉丝，抖音短视频平台已成为“我们媒体”和全媒体矩阵，是客户获取、推广和收入的重要平台之一。兼职副业推荐公众号，配音新手圈，声优配音圈，新配音兼职圈，配音就业圈，鼎音副业，有声新手圈，每天更新各种远程工作与在线兼职，职位包括：写手、程序开发、剪辑、设计、翻译、配音、无门槛、插画、翻译、等等。。。每日更新兼职。但对于初学者来说，如何在抖音上建立自己的品牌，积累粉丝，
  • 云服务业界动态简报-20180128 Captain7
    一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
  • 开微信公众号怎么赚钱？解析盈利策略与实操指南 氧惠_飞智666999
    微信公众号成为了人们获取信息、交流思想的重要平台。越来越多的人选择开设自己的微信公众号，希望通过这一平台实现个人价值或创造经济效益。那么，开微信公众号怎么赚钱呢？本文将为您详细解析微信公众号的盈利策略与实操指南。公众号流量主就找善士导师（shanshi2024）公众号：「善士笔记」主理人，《我的亲身经历，四个月公众号流量主从0到日入过万！》公司旗下管理800+公众号矩阵账号。代表案例如：爸妈领域、
  • GIS数据处理软件：地理信息与遥感领域的智慧引擎 GeoSaaS 地理信息智慧城市数据库人工智能大数据gis
    在地理信息与遥感技术的广阔天地间，数据处理软件如同一座桥接驳岸的智慧引擎，将海量的原始数据转化为决策的金矿，推动着城市规划、环境保护、灾害管理、资源开发等领域的深度变革。本文将深入解析其核心功能、技术前沿、应用实例及未来展望，探析数据处理软件如何为地理信息与遥感技术插上智慧的翅膀。数据处理软件的核心技术与功能矩阵数据清洗与格式转换：自动去除冗余杂乱码、异常值，格式标准化数据，确保后续处理的准确性与
  • 微信公众号如何盈利赚钱?变现模式都能月入过万 氧惠购物达人
    在移动互联网时代，微信公众号成为了众多内容创作者、品牌商家和个人展示自我、传递价值、实现商业变现的重要平台。那么，公众号究竟如何通过运营实现盈利呢？本文将深入剖析公众号赚钱的多种途径，帮助广大运营者找到适合自己的盈利模式。公众号流量主就找善士导师（shanshi2024）公众号：「善士笔记」主理人，《我的亲身经历，四个月公众号流量主从0到日入过万！》公司旗下管理800+公众号矩阵账号。代表案例如：
  • 第二章 按问题编程 ronghuilin 程序特征程序设计
    程序设计的基础，建立计算机编程思维，掌握基本问题的分析，与编写源程序。1.在一组数据中寻找一个元素操作“寻找”在计算机软件中是“搜索”，近几年称为“扫描”。首先应了解这些数据存放在什么结构中。一组数据能存储在线性表(one-to-one)中，每个元素只有一个前趋和后继，常用的是数组array，应用性能高的是栈Stack与队列queue。数学计算在计算机程序中的基础是矩阵计算，矩阵存放在二维数组中。
  • windows C++ 并行编程-编写parallel_for 循环 sului windowsC++并行编程技术c++开发语言
    示例：计算两个矩阵的乘积以下示例显示了matrix_multiply函数，可计算两个方阵的乘积。//Computestheproductoftwosquarematrices.voidmatrix_multiply(double**m1,double**m2,double**result,size_tsize){for(size_ti=0;i#include#include#includeusin
  • 面试经典 150 题 2 —（二分查找）— 74. 搜索二维矩阵 BreezeChasingDrizzle leetcode矩阵算法leetcodec++二分查找
    74.搜索二维矩阵方法classSolution{public:boolsearchMatrix(vector>&matrix,inttarget){intmatrixRows=matrix.size(),matrixCols=matrix[0].size();//先找target所在的行inttargetAtRow=-1;for(inti=0;i>&matrix,inttarget){intma
  • 三点or多点的变换矩阵求解opencv & eigen 合工大机器人实验室 C++矩阵opencv线性代数
    《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》，它使用SVD方法计算T和t。只要算出变换矩阵，就可以算出A坐标系的一个点P在坐标系B里的对应点坐标，即R为3x3的转换矩阵，t为3x1的位移变换向量，这里点坐标均为3x1的列向量（非齐次形式，齐次形式下为4x1列向量，多出的一个元素值补1而已）。理论上只
  • 构建蛋白质复合体结构中所有链序列的同源性矩阵 qq_27390023 生物信息学python
    为了生成蛋白质复合体结构中所有链之间的同源性矩阵，我们可以使用基于结构比对的工具（如TM-align），逐对地比对所有链，并根据比对结果（通常是TM-score）构建同源性矩阵。具体步骤包括：提取每条链的序列：从蛋白质复合体的PDB文件中提取每个链的序列，并保存成单独的文件。使用TM-align进行比对：对每对链进行比对，计算它们的TM-score。构建同源性矩阵：将每对链的TM-score记录到
  • Matlab2024a安装教程 是阿宇呢 信息可视化开发语言
    MATLAB是一款商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分，可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。1.解压安装包：①鼠标右击【MATLABR2024a(64bit)
  • Python【math数学函数】 Alan_Lowe #Pythonpython
    Python【math数学函数】文章目录Python【math数学函数】数论与表示函数1.ceil()和floor()2.comb()3.copysign()4.fabs()5.factorial()6.gcd()7.lcm()幂函数与对数函数1.exp()和math.e和pow()2.log()和log2()和log10()3.sqrt(x)三角函数1.asin、acos()、atan()2.s
  • seurat自学笔记1.0 单细胞数据导入 Sanye2022 pythonpandas
    Python读取.h5ad文件importanndataimportpandasaspdadata=anndata.read("/home/R/R_data/Seurat/PBMC10/output/adata.h5ad")#adata.X.todense()#将稀疏矩阵转成普通矩阵#X=pd.DataFrame(adata.X.todense())#cell_name=adata.obs.ind
  • 蓝桥杯第十四届C++C组 bug～bug～ 蓝桥杯蓝桥杯c++c语言
    目录三国游戏填充翻转【单调队列优化DP】子矩阵【快速幂、欧拉函数】互质数的个数【tire树】异或和之差【质因数分解】公因数匹配子树的大小三国游戏题目描述小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X,Y,Z(一开始可以认为都为0)。游戏有n个可能会发生的事件，每个事件之间相互独立且最多只会发生一次，当第i个事件发生时会分别让X,Y,Z增加Ai,Bi,Ci。当游戏结束时(所有事件的
  • 华南农业大学 OJ数据结构 迷宫问题2(C、C++) 打架戴手表、
    18720迷宫问题（最短路径）时间限制:1000MS代码长度限制:10KB提交次数:0通过次数:0题型:编程题语言:不限定Description迷宫是一个n*m的矩阵，玩家需要迷宫入口(坐标1,1)出发，寻找路径走到出口(n,m)。请判断玩家能否从迷宫中走出，如果能走出迷宫输出，输出最短的路径长度，否则输出-1。输入格式第一行两个整数n和m，代表n行m列。(1typedefstruct{intro
  • 用DESeq2包来对RNA-seq数据进行差异分析 Seurat_Satija
    差异分析的套路都是差不多的，大部分设计思想都是继承limma这个包，DESeq2也不例外。DESeq2是DESeq包的更新版本，看样子应该不会有DESeq3了，哈哈，它的设计思想就是针对count类型的数据。可以是任意features的count数据，比如对各个基因的count，或者外显子，或者CHIP-seq的一些feature，都可以用来做差异分析。使用这个包也是需要三个数据：表达矩阵分组矩阵
  • 华为OD机试 - 单词搜索（Python） AsiaFT. Py华为OD机试AB卷算法python华为od
    题目描述找到它是一个小游戏，你需要在一个矩阵中找到给定的单词。假设给定单词HELLOWORD，在矩阵中只要能找到H->E->L->L->O->W->O->R->L->D连成的单词，就算通过。注意区分英文字母大小写，并且您只能上下左右行走，不能走回头路。输入描述输入第1行包含两个整数n、m(0
  • 哪些公众号可以赚钱？探索盈利的公众号类型 氧惠超好用
    在移动互联网时代，微信公众号已成为自媒体人展现才华、分享知识、传递价值的重要平台。随着公众号数量的不断增加，越来越多的运营者开始探索公众号的盈利模式。那么，究竟哪些公众号可以赚钱呢？本文将为您揭示一些常见的盈利公众号类型。公众号流量主就找善士导师（shanshi2024）公众号：「善士笔记」主理人，《我的亲身经历，四个月公众号流量主从0到日入过万！》公司旗下管理800+公众号矩阵账号。代表案例如：
  • python 实现eulers totient欧拉方程算法 luthane 算法python开发语言
    eulerstotient欧拉方程算法介绍欧拉函数（Euler’sTotientFunction），通常表示为()，是一个与正整数相关的函数，它表示小于或等于的正整数中与互质的数的数目。欧拉函数在数论和密码学中有广泛的应用。欧拉函数的性质1.**对于质数，有φ(p)=p−1∗∗φ(p)=p−1^{**}φ(p)=p−1∗∗。2.**如果是质数的次幂，即n=pkn=p^kn=pk，则φ(n)=pk−
  • java封装继承多态等 麦田的设计者 javaeclipsejvmcencapsulatopn
           最近一段时间看了很多的视频却忘记总结了，现在只能想到什么写什么了，希望能起到一个回忆巩固的作用。     1、final关键字       译为：最终的        &
  • F5与集群的区别 bijian1013 weblogic集群F5
            http请求配置不是通过集群，而是F5；集群是weblogic容器的，如果是ejb接口是通过集群。         F5同集群的差别，主要还是会话复制的问题，F5一把是分发http请求用的，因为http都是无状态的服务，无需关注会话问题，类似
  • LeetCode[Math] - #7 Reverse Integer Cwind java题解MathLeetCodeAlgorithm
    原题链接：#7 Reverse Integer   要求： 按位反转输入的数字 例1： 输入 x = 123, 返回 321 例2： 输入 x = -123, 返回 -321   难度：简单   分析： 对于一般情况，首先保存输入数字的符号，然后每次取输入的末位（x%10）作为输出的高位（result = result*10 + x%10）即可。但
  • BufferedOutputStream 周凡杨
         首先说一下这个大批量，是指有上千万的数据量。      例子：      有一张短信历史表，其数据有上千万条数据，要进行数据备份到文本文件，就是执行如下SQL然后将结果集写入到文件中！      select t.msisd
  • linux下模拟按键输入和鼠标 被触发 linux
    查看/dev/input/eventX是什么类型的事件， cat /proc/bus/input/devices 设备有着自己特殊的按键键码，我需要将一些标准的按键，比如0－9，X－Z等模拟成标准按键，比如KEY_0,KEY-Z等，所以需要用到按键 模拟，具体方法就是操作/dev/input/event1文件，向它写入个input_event结构体就可以模拟按键的输入了。 linux/in
  • ContentProvider初体验 肆无忌惮_ ContentProvider
    ContentProvider在安卓开发中非常重要。与Activity，Service，BroadcastReceiver并称安卓组件四大天王。 在android中的作用是用来对外共享数据。因为安卓程序的数据库文件存放在data/data/packagename里面，这里面的文件默认都是私有的，别的程序无法访问。 如果QQ游戏想访问手机QQ的帐号信息一键登录，那么就需要使用内容提供者COnte
  • 关于Spring MVC项目（maven）中通过fileupload上传文件 843977358 mybatisspring mvc修改头像上传文件upload
    Spring MVC 中通过fileupload上传文件，其中项目使用maven管理。   1.上传文件首先需要的是导入相关支持jar包：commons-fileupload.jar,commons-io.jar 因为我是用的maven管理项目，所以要在pom文件中配置（每个人的jar包位置根据实际情况定） <!-- 文件上传 start by zhangyd-c --&g
  • 使用svnkit api，纯java操作svn，实现svn提交，更新等操作 aigo svnkit
     原文：http://blog.csdn.net/hardwin/article/details/7963318   import java.io.File; import org.apache.log4j.Logger; import org.tmatesoft.svn.core.SVNCommitInfo; import org.tmateso
  • 对比浏览器，casperjs，httpclient的Header信息 alleni123 爬虫crawlerheader
    @Override protected void doGet(HttpServletRequest req, HttpServletResponse res) throws ServletException, IOException { String type=req.getParameter("type"); Enumeration es=re
  • java.io操作 DataInputStream和DataOutputStream基本数据流 百合不是茶 java流
    1，java中如果不保存整个对象，只保存类中的属性，那么我们可以使用本篇文章中的方法，如果要保存整个对象  先将类实例化  后面的文章将详细写到     2，DataInputStream 是java.io包中一个数据输入流允许应用程序以与机器无关方式从底层输入流中读取基本 Java 数据类型。应用程序可以使用数据输出流写入稍后由数据输入流读取的数据。
  • 车辆保险理赔案例 bijian1013 车险
    理赔案例： 一货运车，运输公司为车辆购买了机动车商业险和交强险，也买了安全生产责任险，运输一车烟花爆竹，在行驶途中发生爆炸，出现车毁、货损、司机亡、炸死一路人、炸毁一间民宅等惨剧，针对这几种情况，该如何赔付。 赔付建议和方案： 客户所买交强险在这里不起作用，因为交强险的赔付前提是：“机动车发生道路交通意外事故”； 如果是交通意外事故引发的爆炸，则优先适用交强险条款进行赔付，不足的部分由商业
  • 学习Spring必学的Java基础知识(5)—注解 bijian1013 javaspring
            文章来源：http://www.iteye.com/topic/1123823，整理在我的博客有两个目的：一个是原文确实很不错，通俗易懂，督促自已将博主的这一系列关于Spring文章都学完；另一个原因是为免原文被博主删除，在此记录，方便以后查找阅读。           有必要对
  • 【Struts2一】Struts2 Hello World bit1129 Hello world
    Struts2 Hello World应用的基本步骤 创建Struts2的Hello World应用，包括如下几步： 1.配置web.xml 2.创建Action 3.创建struts.xml，配置Action 4.启动web server，通过浏览器访问   配置web.xml <?xml version="1.0" encoding="
  • 【Avro二】Avro RPC框架 bit1129 rpc
    1. Avro RPC简介 1.1. RPC RPC逻辑上分为二层，一是传输层，负责网络通信；二是协议层，将数据按照一定协议格式打包和解包 从序列化方式来看，Apache Thrift 和Google的Protocol Buffers和Avro应该是属于同一个级别的框架，都能跨语言，性能优秀，数据精简，但是Avro的动态模式（不用生成代码，而且性能很好）这个特点让人非常喜欢，比较适合R
  • lua　set get cookie ronin47 lua cookie
    lua: local access_token = ngx.var.cookie_SGAccessToken if access_token then ngx.header["Set-Cookie"] = "SGAccessToken="..access_token.."; path=/;Max-Age=3000" end
  • java-打印不大于N的质数 bylijinnan java
    public class PrimeNumber { /** * 寻找不大于N的质数 */ public static void main(String[] args) { int n=100; PrimeNumber pn=new PrimeNumber(); pn.printPrimeNumber(n); System.out.print
  • Spring源码学习-PropertyPlaceholderHelper bylijinnan javaspring
    今天在看Spring 3.0.0.RELEASE的源码，发现PropertyPlaceholderHelper的一个bug 当时觉得奇怪，上网一搜，果然是个bug，不过早就有人发现了，且已经修复： 详见： http://forum.spring.io/forum/spring-projects/container/88107-propertyplaceholderhelper-bug
  • [逻辑与拓扑]布尔逻辑与拓扑结构的结合会产生什么? comsci 拓扑
       如果我们已经在一个工作流的节点中嵌入了可以进行逻辑推理的代码,那么成百上千个这样的节点如果组成一个拓扑网络,而这个网络是可以自动遍历的,非线性的拓扑计算模型和节点内部的布尔逻辑处理的结合,会产生什么样的结果呢?    是否可以形成一种新的模糊语言识别和处理模型呢?  大家有兴趣可以试试,用软件搞这些有个好处,就是花钱比较少,就算不成
  • ITEYE 都换百度推广了 cuisuqiang GoogleAdSense百度推广广告外快
    以前ITEYE的广告都是谷歌的Google AdSense，现在都换成百度推广了。   为什么个人博客设置里面还是Google AdSense呢？   都知道Google AdSense不好申请，这在ITEYE上也不是讨论了一两天了，强烈建议ITEYE换掉Google AdSense。至少，用一个好申请的吧。   什么时候能从ITEYE上来点外快，哪怕少点
  • 新浪微博技术架构分析 dalan_123 新浪微博架构
    新浪微博在短短一年时间内从零发展到五千万用户，我们的基层架构也发展了几个版本。第一版就是是非常快的，我们可以非常快的实现我们的模块。我们看一下技术特点，微博这个产品从架构上来分析，它需要解决的是发表和订阅的问题。我们第一版采用的是推的消息模式，假如说我们一个明星用户他有10万个粉丝，那就是说用户发表一条微博的时候，我们把这个微博消息攒成10万份，这样就是很简单了，第一版的架构实际上就是这两行字。第
  • 玩转ARP攻击 dcj3sjt126com r
    我写这片文章只是想让你明白深刻理解某一协议的好处。高手免看。如果有人利用这片文章所做的一切事情，盖不负责。 网上关于ARP的资料已经很多了，就不用我都说了。 用某一位高手的话来说，“我们能做的事情很多，唯一受限制的是我们的创造力和想象力”。 ARP也是如此。 以下讨论的机子有 一个要攻击的机子：10.5.4.178 硬件地址：52:54:4C:98
  • PHP编码规范 dcj3sjt126com 编码规范
    一、文件格式 1. 对于只含有 php 代码的文件，我们将在文件结尾处忽略掉 "?>" 。这是为了防止多余的空格或者其它字符影响到代码。例如：<?php$foo = 'foo';2. 缩进应该能够反映出代码的逻辑结果，尽量使用四个空格，禁止使用制表符TAB，因为这样能够保证有跨客户端编程器软件的灵活性。例
  • linux 脱机管理（nohup） eksliang linux nohupnohup
    脱机管理 nohup 转载请出自出处：http://eksliang.iteye.com/blog/2166699 nohup可以让你在脱机或者注销系统后，还能够让工作继续进行。他的语法如下 nohup [命令与参数] --在终端机前台工作 nohup [命令与参数] & --在终端机后台工作   但是这个命令需要注意的是，nohup并不支持bash的内置命令，所
  • BusinessObjects Enterprise Java SDK greemranqq javaBOSAPCrystal Reports
    最近项目用到oracle_ADF  从SAP/BO 上调用 水晶报表，资料比较少，我做一个简单的分享，给和我一样的新手 提供更多的便利。   首先，我是尝试用JAVA JSP 去访问的。   官方API：http://devlibrary.businessobjects.com/BusinessObjectsxi/en/en/BOE_SDK/boesdk_ja
  • 系统负载剧变下的管控策略 iamzhongyong 高并发
    假如目前的系统有100台机器，能够支撑每天1亿的点击量（这个就简单比喻一下），然后系统流量剧变了要，我如何应对，系统有那些策略可以处理，这里总结了一下之前的一些做法。 1、水平扩展 这个最容易理解，加机器，这样的话对于系统刚刚开始的伸缩性设计要求比较高，能够非常灵活的添加机器，来应对流量的变化。 2、系统分组 假如系统服务的业务不同，有优先级高的，有优先级低的，那就让不同的业务调用提前分组
  • BitTorrent DHT 协议中文翻译 justjavac bit
    前言 做了一个磁力链接和BT种子的搜索引擎 {Magnet & Torrent}，因此把 DHT 协议重新看了一遍。 BEP: 5Title: DHT ProtocolVersion: 3dec52cb3ae103ce22358e3894b31cad47a6f22bLast-Modified: Tue Apr 2 16:51:45 2013 -070
  • Ubuntu下Java环境的搭建 macroli java工作ubuntu
    配置命令： 　　$sudo apt-get install ubuntu-restricted-extras 　　再运行如下命令： 　　$sudo apt-get install sun-java6-jdk 　　待安装完毕后选择默认Java. 　　$sudo update- alternatives --config java 　　安装过程提示选择，输入“2”即可，然后按回车键确定。
  • js字符串转日期（兼容IE所有版本） qiaolevip TODateStringIE
    /** * 字符串转时间（yyyy-MM-dd HH:mm:ss） * result （分钟） */ stringToDate : function(fDate){ var fullDate = fDate.split(" ")[0].split("-"); var fullTime = fDate.split("
  • 【数据挖掘学习】关联规则算法Apriori的学习与SQL简单实现购物篮分析 superlxw1234 sql数据挖掘关联规则
    关联规则挖掘用于寻找给定数据集中项之间的有趣的关联或相关关系。 关联规则揭示了数据项间的未知的依赖关系，根据所挖掘的关联关系，可以从一个数据对象的信息来推断另一个数据对象的信息。 例如购物篮分析。牛奶 ⇒ 面包 [支持度：3%，置信度：40%] 支持度3%：意味3%顾客同时购买牛奶和面包。 置信度40%：意味购买牛奶的顾客40%也购买面包。 规则的支持度和置信度是两个规则兴
  • Spring 5.0 的系统需求，期待你的反馈 wiselyman spring
                   Spring 5.0将在2016年发布。Spring5.0将支持JDK 9。          Spring 5.0的特性计划还在工作中，请保持关注，所以作者希望从使用者得到关于Spring 5.0系统需求方面的反馈。  
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他