足球运动员的数据分析实战(python)
一、本案例的相关说明
本人把这篇文章拿出来进行写作的主要原因是为了让大家对数据分析有一个较为清楚的认识,其实数据分析并不是那么高深,只是看你怎么从一堆杂乱无章的数据中能够发现一定的有规律性的结论,有时候可能会觉得某些结论有些牵强,但这属于每个人对每个问题而见解不同,因而较强的数据分析能力,需要我们在实际工作中进行慢慢培养出来。同时这篇文章很好的将pandas库运用到其中,这个也可以帮助我们学以致用,用而学,会起到更好的效果。
1、案例背景
足球运动是最受欢迎的运动之一。在此万受瞩目的运动下,打算针对足球运动员个人的信息,技能水平等各项指标进行相关的分析与统计。例如,我们可能会关注如下的内容:
- 足球运动员是否受出生日期的影响?
- 左撇子适合踢足球吗?
- 足球运动员的号码是否与位置相关?
- 足球运动员的年龄与能力具有怎样的关联?
2、任务说明
目前,我们收集到了某年现役运动员的数据集data.csv。我们希望通过该数据集,针对众多的足球运动员进行分析与统计,从而能够发现一些关于足球运动员的特征,解开我们上述疑问。
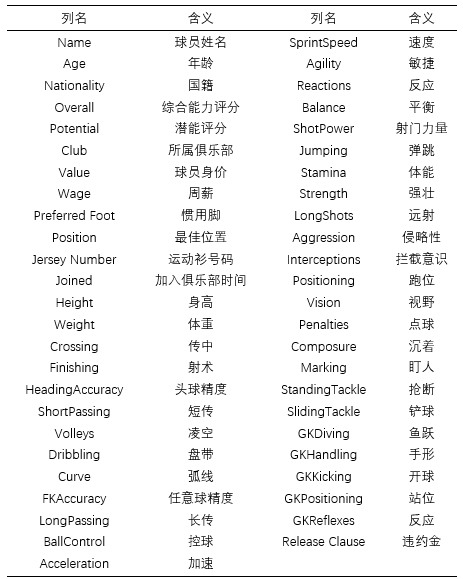
3、数据列名的含义
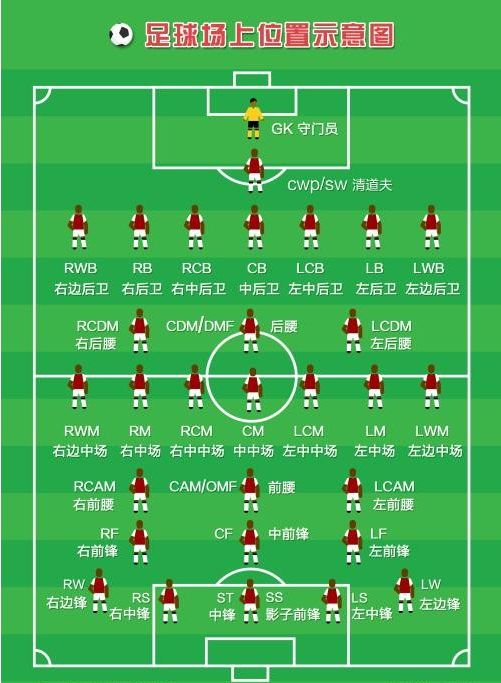
4、足球场上各位置说明
5、什么是数据分析?
数据分析指的就是利用统计学知识,对一系列杂乱无章的数据进行数据分析前的预处理,同时结合数据的具体应用场景,提炼出数据中的有效信息,帮助我们定位、分析、解决某些问题,高效决策。
6、数据分析的基本流程
明确需求
数据收集
内部数据
购买数据
爬取数据
调查问卷
数据预处理
数据清洗
缺失值
异常值
重复值
数据转换
数据分析
数据建模
数据可视化
编写报告
7、理解流程
现在网上最常见的一种比喻数据分析流程的方式,就是利用“炒菜”来对比“数据分析的每个流程”。
| 做菜步骤 | 数据分析步骤 |
|---|---|
| 确定做菜 | 明确需求与目的 |
| 买菜 | 数据收集 |
| 洗菜 | 数据清洗 |
| 切菜 | 数据转换 |
| 炒菜 | 数据分析 |
| 盛菜 | 数据可视化 |
| 写日记 | 编写报告 |
1)熟悉数据集
熟悉数据集,就是在进行数据处理之前,应该先熟悉数据,只有对数据充分熟悉之后,才能更好的进行分析。
熟悉数据常用的方法和属性有shape、head()、tail()、sample()、info()、describe()。
- shape:以元组形式返回数据集的行、列大小。
- head()或tail():当数据量过大时,我们不可能直接查看所有数据,这样会很消耗电脑内存,因此,使用head()或tail(),可以默认返回数据集的前五行、后五行的数据;当向head()或tail()中传入整数n时,则可以返回任意前n行、后n行的数据。
- sample():向方法中传入整数n时,则会从当前数据集中随机抽样n条记录显示出来,对于我们了解数据很有帮助。
- info():可以显示每列的列名、非空值数量、数据类型,内存占用等信息。
- describe():可以帮助我们掌握数值的分布情况,会返回每个字段的count()、mean()、std()、min()、25%、50%、75%、max()。对于非数值型字段,只会显示count()计数。
2)缺失值处理
缺失值就是由于某些原因导致部分数据为空。进行缺失值处理之前,首先应该查看是否有缺失值。
① 检查缺失值的办法:一般有以下两种处理方式;
- 1、通过info查看数据信息。
- 2、可以通过isnull与sum结合,查看缺失值情况。
data.info()
data.isnull().sum(axis=0)
② 缺失值的处理办法:一般也有两种处理方式;
- 1、直接删除(当某一列或某一行存在大量的缺失值的时候)。
- 2、采用某个值填充。
③ 直接删除缺失值
采用dropna()方法,默认删除所有含有缺失行的数据(即:某一行只有要一个字段缺失,就删除)。传入参数how=”all”,只删除那些全为空的行。
# inplace=True表示原地修改数据集
data.dropna(axis=0, inplace=True)
# 对删除后缺失值后的数据集,再次进行缺失值统计
data.isnull().sum(axis=1)
④ 填充
可以采用均值、中位数、众数、附近值进行填充。
对于缺失值填充,这里做一个简单的说明:1、当数据服从正态分布,这时候可以采用均值填充;2、当数据为偏态分布(不管左偏还是右偏),则采用中位数进行填充;3、若某个字段为离散型数据,则最好采用众数填充;4、若像温度这样的数据,前后时刻之间的温度关联肯定是最大的,这时采用前后时刻温度进行填充更好。
3)异常值处理
异常值:就是和正常数据相比,过高或者过低的数据。
异常值检测:对异常值进行检测,主要有以下几种方式:1、根据业务需求和经验对不同指标所划分的范围,超过指定范围的数据叫做异常值;2、绘制箱线图,大于上边缘和小于下边缘的数据叫做异常值;3、通过descride()函数,可以找出数据的25%和75%分位数,然后把“小于q1+1.5IQR,大于q3+1.5IQR”的数据叫做异常值,q1为25%分位数,q3为75%分位数,IQR= q3- q1的差值。
异常值处理:主要有三种处理办法。1、直接删除;2、把异常值当做缺失值填充;3、把异常值当做特殊情况,研究异常值出现的原因。
4)重复值处理
重复数据,指的是数据集中同样的记录有多条。对于这样的数据一般就是直接删除。
重复值的检测:data.duplicated().sum()可以查看,重复数据有多少行。
重复值的删除:data.drop_duplicates(inplace=True)。
上述函数可以配合使用参数subset=[]和keep进行调整,具体需要的时候,再百度自学。
二、数据分析代码
1、导入相关的库
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
# 用来显示中文标签
mpl.rcParams["font.family"] = "SimHei"
# 用来显示负号
mpl.rcParams["axes.unicode_minus"] = False
# 有时候运行代码时会有很多warning输出,像提醒新版本之类的,如果不想这些乱糟糟的输出,可以使用如下代码
warnings.filterwarnings('ignore')
2、读取data.csv数据集
① 读取数据集
data = pd.read_csv("G:\\2大数据学习\\data.csv",engine="python",encoding="utf-8-sig")
- 当文件路径中存在中文时,需要设置engine参数来指定默认引擎为python,否则会报错。
- utf-8-sig这个编码在windows系统中是常见的。不带有BOM格式的数据才是标准的utf8,但是在windows下,用记事本打开一个文本文件,另存为utf-8格式后,该文件开头就会被带上BOM头信息。这个时候当我们指定编码为utf8,会报错,因此我们就需要指定编码为utf-8-sig,告诉系统该文件的编码是带有BOM格式的utf8编码文件。
② 熟悉数据集的几种方式
# 查看数据集共有多少行、多少列
data.shape
# 查看数据集的前5行
data.head()
# 查看数据集的后5行
data.tail()
# 随机从数据集中抽取5行,显示
data.sample(5)
# 显示每列的列名、非空值数量、数据类型,内存占用等信息。
data.info()
# 此函数可以帮助我们掌握数据的分布情况
data.describe()
注意:head()、tail()和sample()方法中都可以传入一个整数值,head(10)表示显示前10行,tail(10)表示显示后10行,sample(10)表示任意抽取10行显示。
③ 设置DataFrame最大显示列数
DataFrame在显示数据时,若列数较多,中间会将一些列省略掉,变为省略号,而我们往往又需要查看全部列的情况,这个时候就需要设置DataFrame最大显示列数。
pd.set_option("display.max_columns",500)
④ 选取指定列,进行相关的数据分析
有时候,数据集中的列,并非都是我们分析所需要的,我们可以有选择性的进行加载,只加载我们需要的信息列(特征列)。
columns = ["Name", "Age", "Nationality", "Overall", "Potential", "Club",
"Value", "Wage", "Preferred Foot","Position", "Jersey Number",
"Joined","Height", "Weight", "Crossing","Finishing","HeadingAccuracy",
"ShortPassing", "Volleys","Dribbling", "Curve","FKAccuracy","LongPassing",
"Jumping","Stamina","Strength","Aggression","Interceptions","Positioning",
"Vision","Penalties","Marking","StandingTackle", "SlidingTackle","GKDiving",
"GKHandling","GKKicking","GKPositioning", "GKReflexes", "Release Clause"]
pd.read_csv("G:\\2大数据学习\\data.csv",engine="python",encoding="utf-8-sig",usecols=columns)
# 查看数据集共有多少行、多少列
data.shape
# 查看数据集的前5行
data.head()
# 查看数据集的后5行
data.tail()
# 随机从数据集中抽取5行,显示
data.sample(5)
# 显示每列的列名、非空值数量、数据类型,内存占用等信息。
data.info()
# 此函数可以帮助我们掌握数据的分布情况
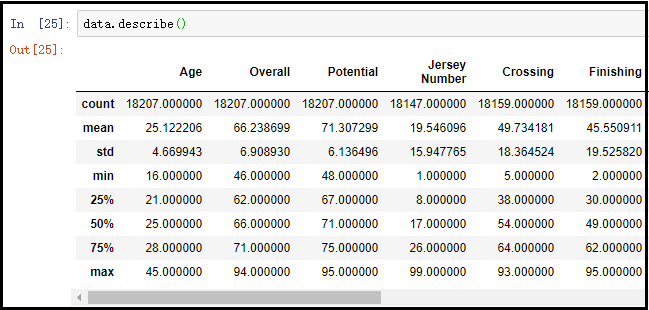
data.describe()
info()方法的结果显示如下:

截取describe()方法的部分结果如下:
3、缺失值处理
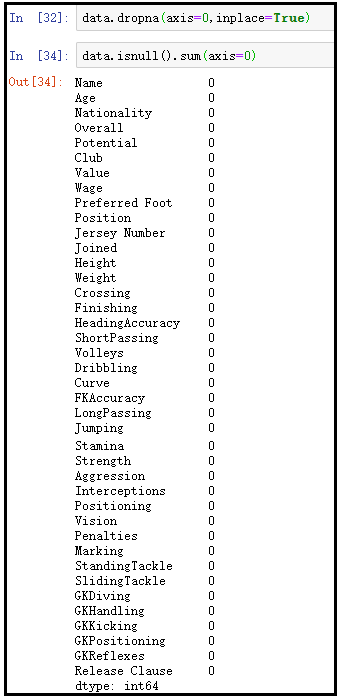
1)查看缺失值
data.info()
data.isnull().sum(axis=0)
结果如下:
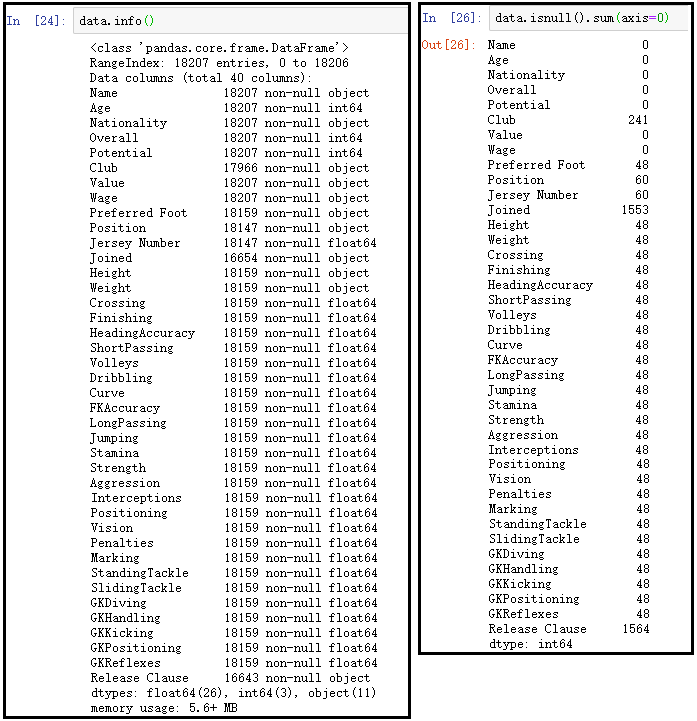
结果分析:通过上面的展示可以发现,info()方法虽然可以看到哪些字段具有缺失值,但是并不直观。通过data.isnull().sum(axis=0)结果显示,可以很清楚的看到哪些字段具有缺失值,有多少个缺失值。
2)删除缺失值
data.dropna(axis=0,inplace=True)
data.isnull().sum(axis=0)
4、异常值处理
① info()方法展示出的信息
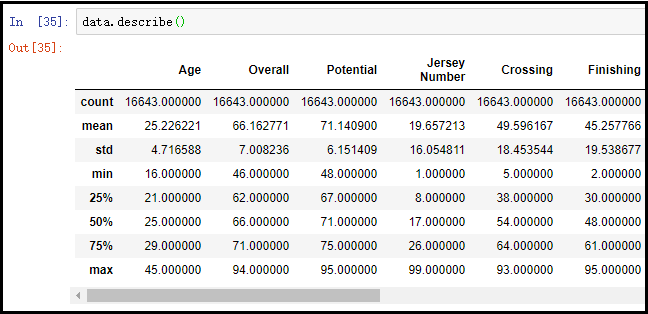
结果分析:上图截取了部分列的结果展示,其中count表示非空记录数;mean表示该列所有数据的均值;std表示该列所有数据的标准差;min表示该列数据中的最小值;max表示该列数据中的最大值;25%表示该列中有1/4的数据,小于该值;50%表示该列中有1/2的数据,小于该值;75%表示该列中有3/4的数据,小于该值;
② 利用箱线图,查看异常值
由于数据集列数太多,因此我随意选取两列画出其箱线图进行展示。
sns.boxplot(data=data[["Age", "Overall"]])
结果如下:
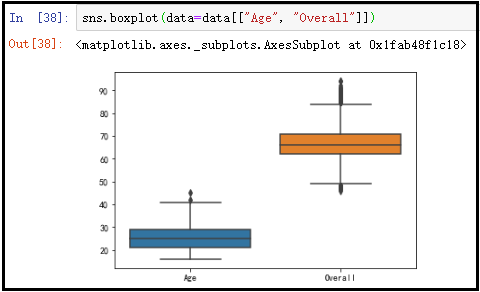
结果分析:此数据集主要是一些打分情况,几乎没有什么特别的异常值,同时有时候一些异常值数据的产生也是合理的,并不是能够随意删除的,因此实际生产中,可以按照上述介绍的方法,结合实际业务进行异常值的处理。
5、重复值处理
data.duplicated().sum()
# data.drop_duplicates(inplace=True)
结果如下:
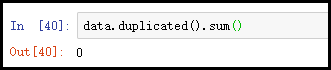
结果分析:从上面的结果中可以看出,此数据集中没有重复的数据,duplicated()函数默认是将两行完全一样的记录,称之为“重复值”,当然此函数还有一些其他参数,供我们选择,你可以根据需求,随意指定某两行数据有多少个字段相同,可以称之为“重复值”。当数据集中含有重复值的时候,可以使用这句代码data.drop_duplicates(inplace=True)原地删除数据集中的重复值。
6、足球运动员的身高体重分布
1)数据转换
想要统计身高与体重的分布情况,由于数据集中的身高与体重数据并不是我们熟悉的身高与体重的单位,同时也并不是数值类型的数据,因此处理之前需要我们先做数据转换。
- 1英尺 = 30.48厘米
- 1英寸 = 2.54厘米
- 1磅 = 0.45千克
def tran_height(height):
v = height.split("'")
return int(v[0])*30.48 + int(v[1])*2.54
def tran_weight(weight):
v = int(weight.replace("lbs", ""))
return v*0.45
2)绘制核密度图
fig, ax = plt.subplots(1, 2)
fig.set_size_inches((18, 5))
sns.distplot(data[["Height"]], bins=50, ax=ax[0], color="g") sns.distplot(data["Weight"], bins=50, ax=ax[1])
结果如下:

结果分析:通过上图展示可以发现,足球运动员的身高和体重的分布近似呈现正态分布,这个也与显示情况相似,身高和体重处在两端的人数较少,处在均值附近的人数最多。当数据量足够大的时候,根据中心极限定理可以知道,数据集的结果几乎呈现一个正态分布。
7、左撇子适合踢足球吗?
1)数量上对比
number = data["Preferred Foot"].value_counts()
display(number)
sns.countplot(x="Preferred Foot", data=data)
结果如下:

结果分析:Preferred Foot这个字段指的是足球运动员的惯用脚,通过上图展示的左脚和右脚的数量上的对比分析可以发现,左脚人数明显多于右脚的人数。
2)能力上对比
data.groupby("Preferred Foot")["Overall"].mean()
sns.barplot(x="Preferred Foot", y="Overall", data=data)
结果如下:
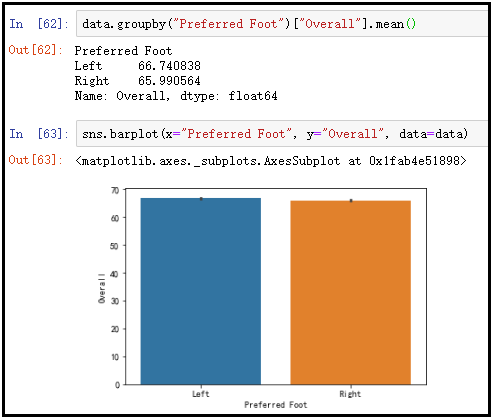
结果分析:Overall这个字段指的是足球运动员的综合能力评分,这里我们将子球运动员的惯用脚进行分组后,求出足球运动员的综合能力评分,可以看出左脚和右脚的综合能力得分,没有太大区别。
3)位置上对比
由于在综合能力上体现不明显,我们现在通过每个位置,进行更细致的分析。为了分析的客观性,我们只统计左脚与右脚都超过50人(含50人)的位置。
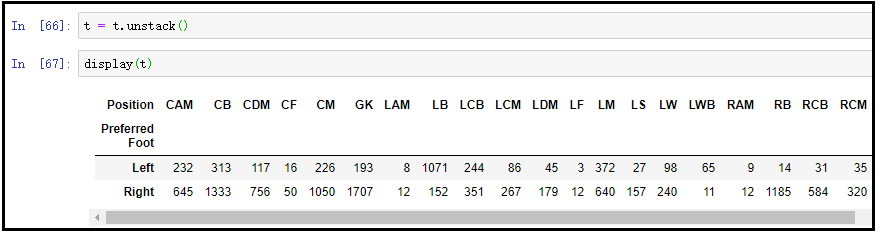
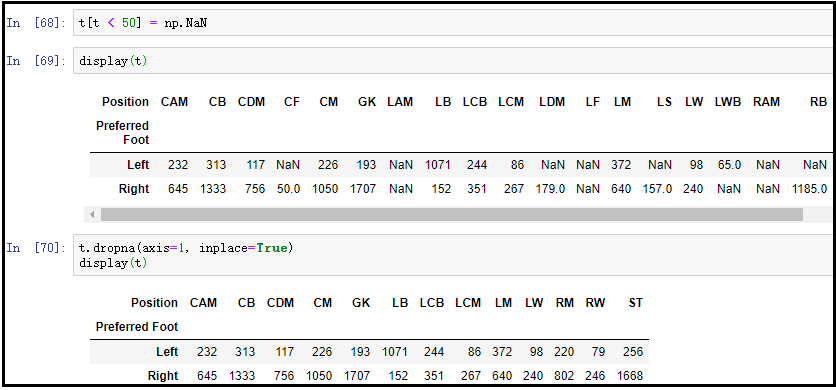
① 首先,计算哪些位置左右脚球员都达到了50人。
t = data.groupby(["Preferred Foot", "Position"]).size()
t = t.unstack()
t[t < 50] = np.NaN t.dropna(axis=1, inplace=True)
display(t)
结果如下:

② 然后,我们根据之前计算的那些位置,对数据集进行过滤。
display(t.columns)
t2 = data[data["Position"].isin(t.columns)]
plt.figure(figsize=(18, 10))
sns.barplot(x="Position", y="Overall", hue="Preferred Foot", hue_order=["Left", "Right"], data=t2)
结果如下:
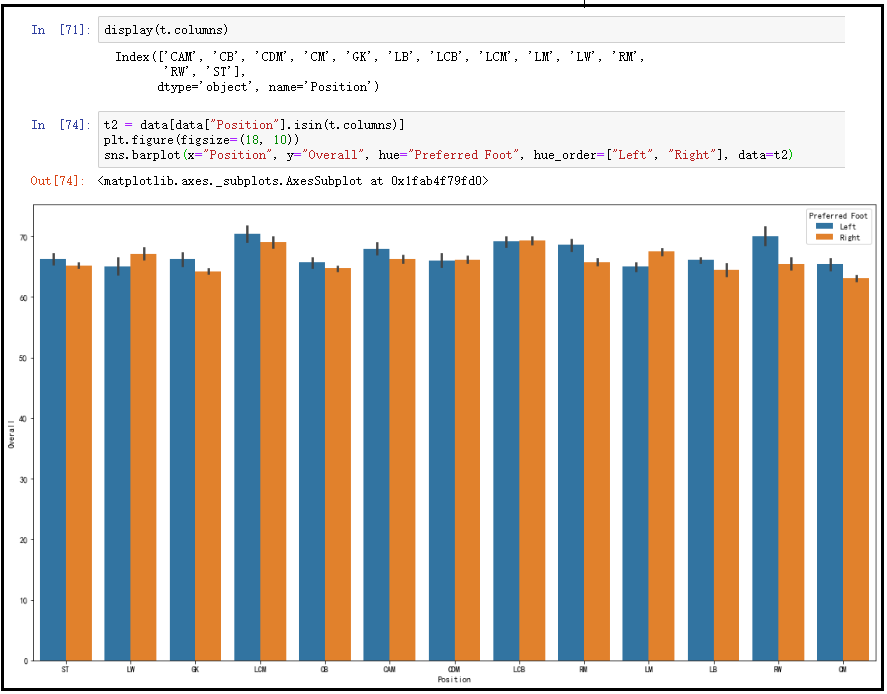
结果分析:从上图中可以清晰地看出,左脚选手更适合RW(右边锋)的位置。而在其他位置上,左右脚的人数差别并没有显著性的差异。
8、哪个的俱乐部、国家拥有综合能力更好的球员(展示top10)。
由于每个俱乐部、国家队足球年动员的人数不一,为了统计的客观性,只考虑人数达到一定规模的俱乐部、国家。
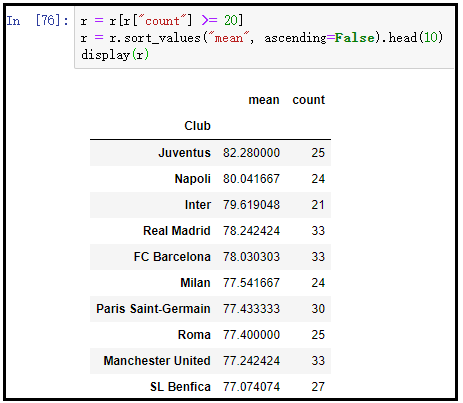
1)俱乐部
g = data.groupby("Club")
r = g["Overall"].agg(["mean", "count"])
r = r[r["count"] >= 20]
r = r.sort_values("mean", ascending=False).head(10)
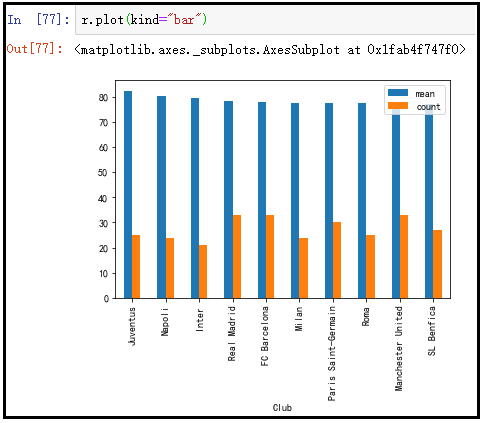
display(r)
r.plot(kind="bar")
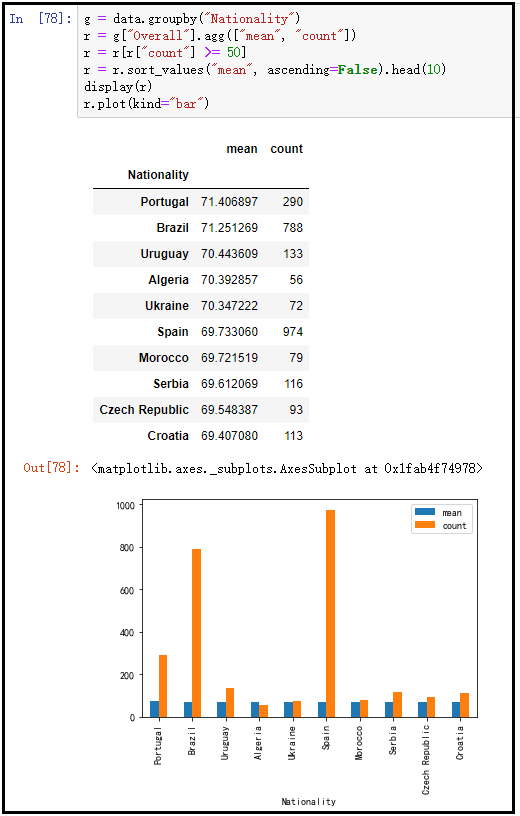
2)国家队
g = data.groupby("Nationality")
r = g["Overall"].agg(["mean", "count"])
r = r[r["count"] >= 50]
r = r.sort_values("mean", ascending=False).head(10)
display(r)
r.plot(kind="bar")
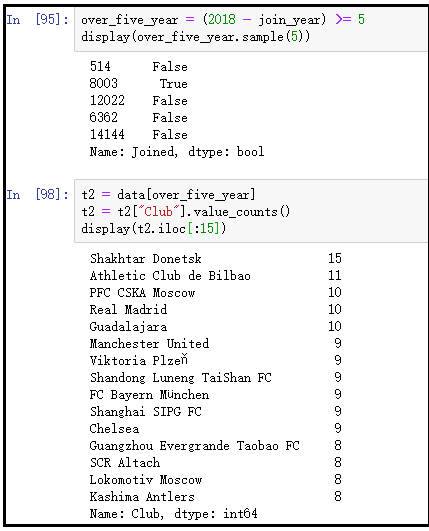
9、哪些俱乐部拥有效力更久的球员(5年及以上)?
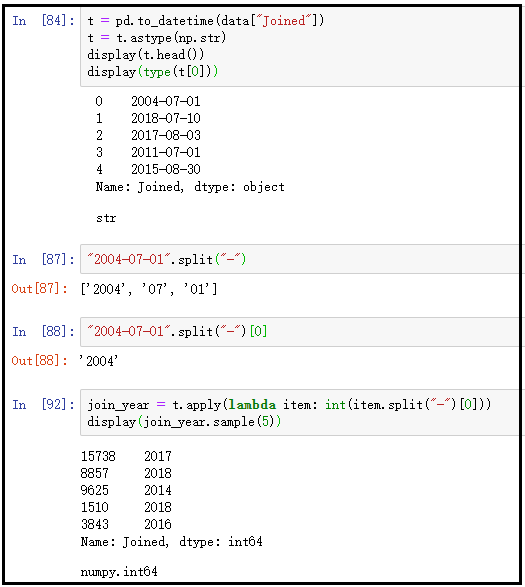
t = pd.to_datetime(data["Joined"])
t = t.astype(np.str)
join_year = t.apply(lambda item: int(item.split("-")[0]))
over_five_year = (2018 - join_year) >= 5
t2 = data[over_five_year]
t2 = t2["Club"].value_counts()
display(t2)
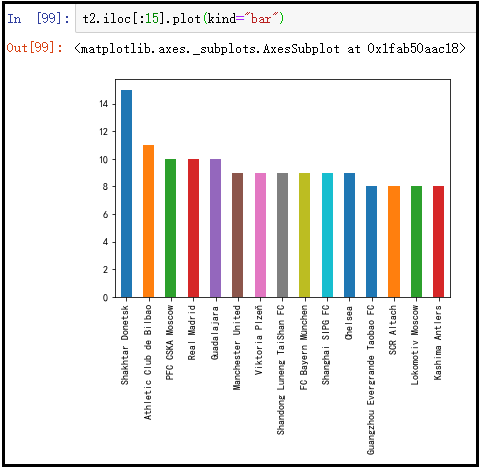
t2.iloc[:15].plot(kind="bar")
10、足球运动员是否是出生日期相关?
我们现有的数据集中,不含有具体的出生日期,因此,我们使用另外一个数据集,该数据集包含2018年世界杯所有球员。
代码如下:
data2 = pd.read_csv("G:\\2大数据学习\\wc2018-players.csv",engine="python",encoding="utf-8-sig")
data2.head()
t = data2["Birth Date"].str.split(".", expand=True)
t[0].value_counts().plot(kind="bar")
t[1].value_counts().plot(kind="bar")
t[2].value_counts().plot(kind="bar")
结果如下:
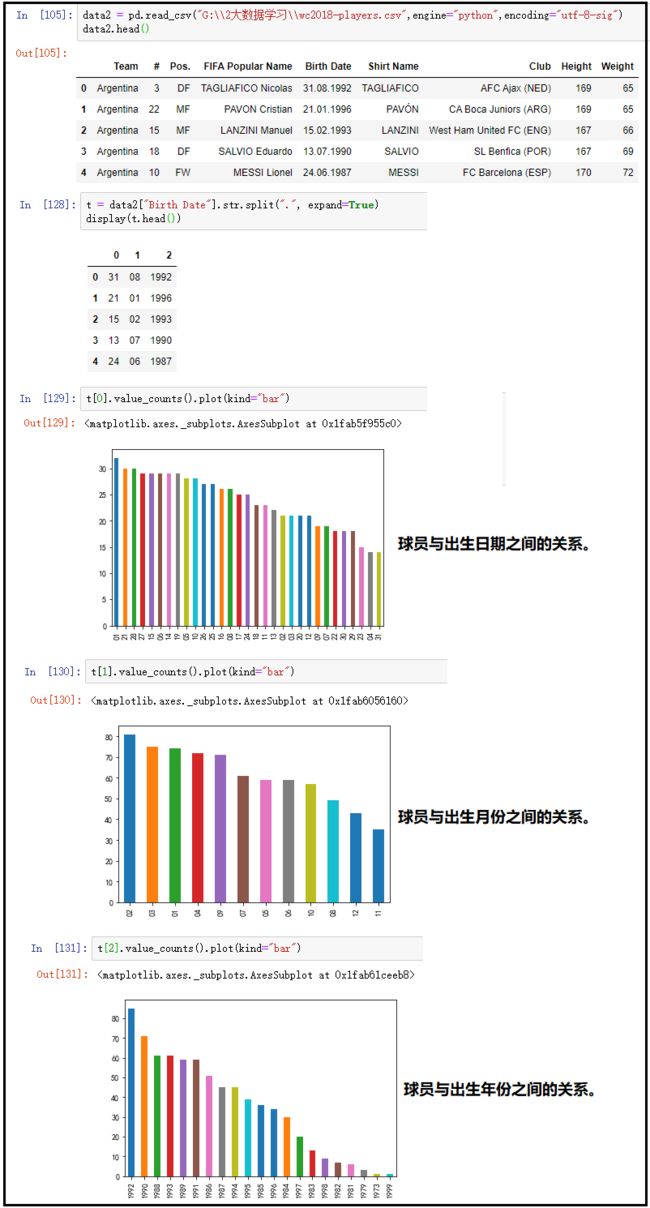
结论如下:对于球员与出生日期这张图,并看不出一定的规律性,由于样本量并不够大,不同日期的球员数量差别10个左右,并不能说明什么问题。对于球员与出生月份这张图,可以看出年初出生的运动员比年尾出生的运动员多,由于年初出生的运动员和年尾出生的运动员,都是同一年的,但是年初出生的运动员比年尾出生的运动员,要多学习了那么几个月,因此能力稍微更强、更有一些经验,因此在同龄人选拔的时候,会更有优势一些(这个是概率问题,并不是说年尾出生的运动员优秀的不多)。对于球员与出生年份这张图,可以看出本阶段球员中1992年出生的球员最多,1999出生的球员最少。
足球运动员与出生日期是有关的,在年初出生的运动员要明显多于在年末出生的运动员。
11、足球运动员号码是否与位置相关?
g = data.groupby(["Jersey Number", "Position"])
t = g.size()
#display(t)
t = t[t >= 100]
t.plot(kind="bar")
结果如下:
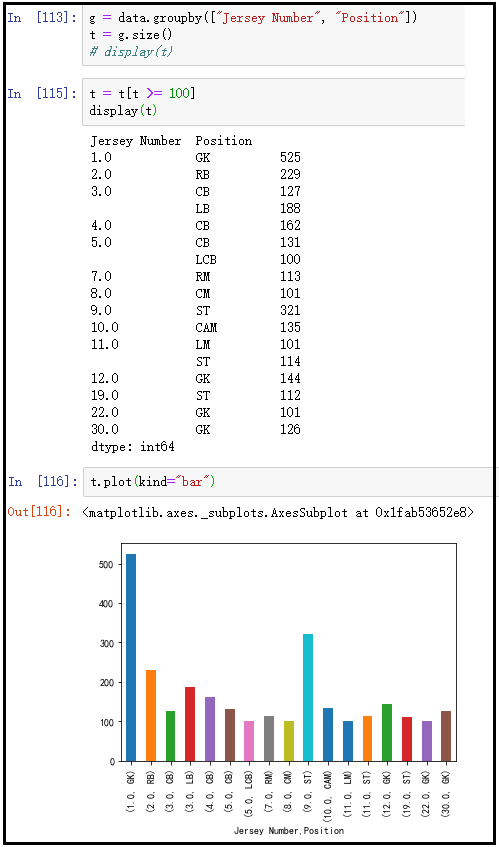
结论如下:球员的号码与位置是相关的,例如,1号通常都是守门员,9号通常是中锋等,这个在图中有着很好的体现。
12、身价与薪水,违约金是否相关?
因为身价与违约金的单位既有M,也有K,为了便于分析,我们统一使用K作为单位,同时,将类型转换为数值类型,便于统计。
def to_numeric(item):
item = item.replace("€", "")
value = float(item[:-1])
if item[-1] == "M":
value *= 1000
return value
data["Value"] = data["Value"].apply(to_numeric)
data["Wage"] = data["Wage"].apply(to_numeric)
data["Release Clause"] = data["Release Clause"].apply(to_numeric) data.head()
sns.scatterplot(x="Value", y="Wage", data=data)
sns.scatterplot(x="Value", y="Release Clause", data=data)
sns.scatterplot(x="Value", y="Height", data=data)
结果如下:

结论如下:从上图可以看出,足球运动员的身价与薪水和违约金均存在一定的线性关系,但是身价和违约金的线性关系更强(具体是什么样的线性关系,就需要建模了)。因此可以得出足球运动员的身价与其薪水是紧密关联的,尤其是违约金,与身价的关联更大。最下面这张图是随意画的球员身价与升高的关系,可以看出球员身价与升高并没有什么关系。
13、哪些指标对综合评分的影响较大?
plt.figure(figsize=(25, 25))
sns.heatmap(data.corr(), annot=True, fmt=".2f", cmap=plt.cm.Greens)
plt.savefig("corr.png", dpi=100, bbox_inches="tight")
这张图就不展示结果了,由于图太大。
14、年龄与评分具有怎样的关系?
sns.scatterplot(x="Age", y="Overall", data=data)
data["Age"].corr(data["Overall"])
# 对一个数组进行切分,可以将连续值变成离散值。
# bins 指定区间数量(桶数)。bins如果为int类型,则进行等分。此处的区间边界与为前开后闭。
# pd.cut(t["Age"], bins=4)
# 如果需要进行区间的不等分,则可以将bins参数指定为数组类型。数组来指定区间的边界。
min_, max_ = data["Age"].min() - 0.5, data["Age"].max()
# pd.cut(t["Age"], bins=[min_, 20, 30, 40, max_])
# pd.cut 默认显示的内容为区间的范围,如果我们希望自定义内容(每个区间显示的内容),可以通过labels参数进行指定。
t = pd.cut(data["Age"], bins=[min_, 20, 30, 40, max_], labels=["弱冠之年", "而立之年","不惑之年","知天命"])
t = pd.concat((t, data["Overall"]), axis=1)
g = t.groupby("Age")
display(g["Overall"].mean())
sns.lineplot(y="Overall", marker=" ", ms=30, x="Age", data=t)
结果如下:
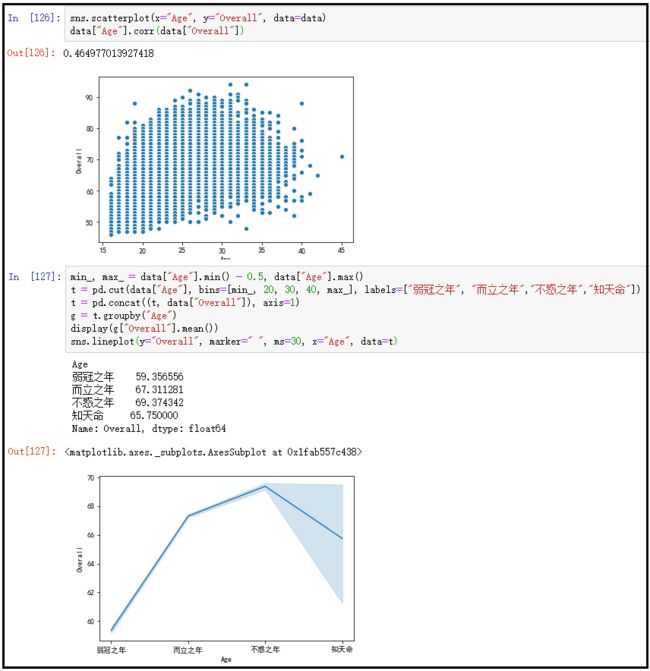
结论如下:运动员随着年龄的增长,球员得到更多的锻炼与经验,总体能力提升,综合能力评分因此也不断增长,但三十几岁之后,由于体力等其它因素的影响,综合能力评分呈现下降趋势。