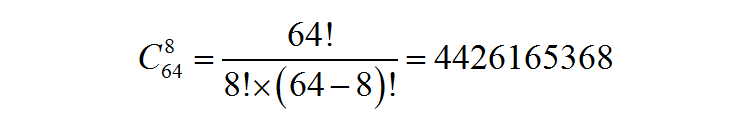后宫佳丽三千，皇后只有一个

^第13届智能车竞赛总决赛颁奖舞台 | 姚祖婵供图^

智能车竞赛

是八皇后问题，参赛车模作品在8×8的棋格内将原本随机分布的八个棋子进行搬移，最终使其满足“八皇后”约束-即在同一行、同一列、同一正反斜对角线上只有一个棋子。比赛胜负是以参赛车模启动进入场地，直至完成任务退出场地位置的时间来衡量，用时少者胜出。

^随机分布八个棋子的初始位置 | 比赛软件^

规则没有限制车模进入场地的位置，在比赛棋子分布后，参赛队伍 有两分钟的出发前的准备时间。

在百度百科的“八皇后问题”词条中记录了该问题是由国际象棋手马克思.贝瑟尔与1848年（欧洲发生革命）提出的，后经使用图论方法和计算机回溯算法可以寻找出92中满足八皇后约束的结果。

^八皇后的92种结果 | 比赛软件显示^

如果棋子在棋盘格中的起始位置为随机分布，所有可能的初始棋局数量为：

如果限制起始时每一行，每一列只有一个棋子，那么可能的初始棋局数量为：

这些棋局移动到最接近92种满足八皇后位置约束的搬移棋子距离是各不相同的。

^{从随机起始位置使用最少步数满足八皇后约束}

对于起始位置满足每一行、每一列只有一个棋子的初始位置，可以统计出全部40320个情形所需最少移动步数分布。

^{起始位置满足每行每列只有一个棋子的起始位置移动的最小步数统计}

移动步数最少为0布，即初始位置就满足八皇后约束条件。最大步数为20步，没有奇数移动步数。频次最高的是移动六步。

由于完全随机（但限制每一棋格内只有一个棋子）的初始位置非常多，至少使用我的计算机还无法短期内统计完，所以就随机抽取了10万次起始位置，统计最少移动步数的分布，如下图所示：

^{初始位置完全随机情况下的移动步数概率分布}

从上图可以看出，移动步数的最高概率由原来的6步，增加到了12步，这是由于起始位置已经不再限制每行每列只有一个棋子的原因。

因此，为了保证创意比赛预赛阶段，八皇后问题比赛的公平性，每一支队伍的初始位置需要各不相同，但距离八皇后结果所需要移动的最少步数应该相同。比如，都需要12（或者其他的数字）。

在实际棋子搬运过程中，车模需要平移，转弯。对于某些类型的车模，完成转弯动作所需要的时间比平移要慢，因此在比赛中，除了考虑到移动棋子的距离（步数）之外，还需要考虑转弯的次数。

对于前面所有需要移动12步的初始情况，统计其中需要转弯的次数，分布如下：

^{需要移动12次情况下所需要转弯的次数统计}

可以看出，大部分的初始情况需要车模完成0_{4转弯，及少数情况则需要移动5}6次的转弯。

综合考虑以上情形，在选择八皇后初始位置的时候，需要同时指定所需要的移动最少步数和转弯次数。下图显示了三次计算机通过随机抽样，获得移动步数为15次，转弯次数为3次的八皇后初始化位置。

^{计算机选择八皇后初始化位置}

当然了，对于创意比赛中，最为激烈和有趣的过程，还当属双方斗智斗勇的Quoridor对弈阶段。上面的八皇后问题还可以通过计算机软件完成最优移动搜索，但对于对弈阶段则需要双方参赛队伍依靠自己的智慧和车模的力量完成对抗比赛。

^{Quoridor对抗计时软件界面}

创意比赛的软件可以在公众号中输入以下五个字母可以直接跳转至下载链接：

?eqiv也可以在下面百度网盘进行下载：

https://pan.baidu.com/s/13BgAqUkmQwCcGn-rH149mQ

对于创意比赛大家还有什么意见和建议，欢迎在“留言”中给出。