scikit-learn：回归分析——多重共线性：岭回归与Lasso

1 最熟悉的陌生人：多重共线性

推导了多元线性回归使用最小二乘法的求解原理，我们对多元线性回归的损失函数求导，并得出求解系数 的式子和过程：

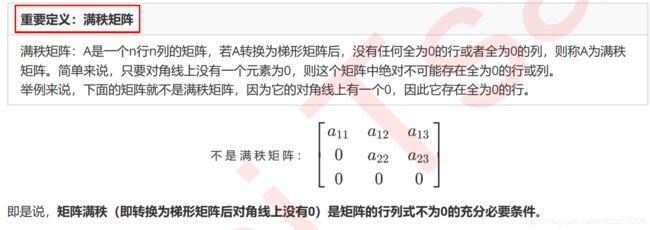
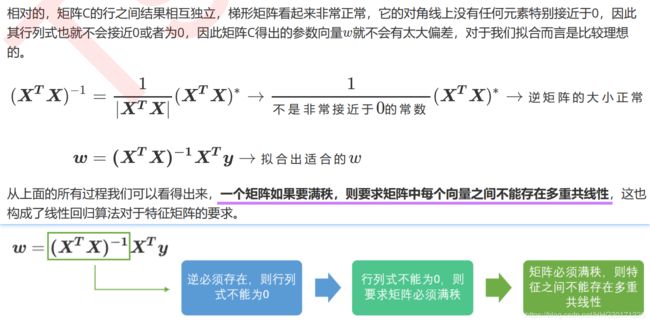
在现实中特征之间完全独立的情况其实非常少，因为大部分数据统计手段或者收集者并不考虑统计学或者机器学习建模时的需求，现实数据多多少少都会存在一些相关性，极端情况下，甚至还可能出现收集的特征数量比样本数量多的情况。通常来说，这些相关性在机器学习中通常无伤大雅（在统计学中他们可能是比较严重的问题），即便有一些偏差，只要最小二乘法能够求解，我们都有可能会无视掉它。毕竟，想要消除特征的相关性，无论使用怎样的手段，都无法避免进行特征选择，这意味着可用的信息变得更加少，对于机器学习来说，很有可能尽量排除相关性后，模型的整体效果会受到巨大的打击。这种情况下，我们选择不处理相关性，只要结果好，一切万事大吉

2 岭回归

2.1 岭回归解决多重共线性问题

2.2 linear_model.Ridge

在sklearn中，岭回归由线性模型库中的Ridge类来调用：

class sklearn.linear_model.Ridge (alpha=1.0, #正则化系数
								fit_intercept=True, 
								normalize=False, 
								copy_X=True, 
								max_iter=None,	#最大迭代系数
								tol=0.001, 
								solver=’auto’, 	#解决方法，除了最小二乘法之外的
								random_state=None
		)

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing as fch
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split as TTS

housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数", "房屋使用年代中位数", "平均房间数目"
    , "平均卧室数目", "街区人口", "平均入住率", "街区的纬度", "街区的经度"]
X.head()
Xtrain, Xtest, Ytrain, Ytest = TTS(X, y, test_size=0.3, random_state=420)
# 数据集索引恢复
for i in [Xtrain, Xtest]:
    i.index = range(i.shape[0])
# 使用岭回归来进行建模
reg = Ridge(alpha=1).fit(Xtrain, Ytrain)

sc = reg.score(Xtest, Ytest)
print(sc)  # 0.6043610352312279

# 交叉验证下，与线性回归相比，岭回归的结果如何变化？
alpharange = np.arange(1, 1001, 100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg, X, y, cv=5, scoring="r2").mean()
    linears = cross_val_score(linear, X, y, cv=5, scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
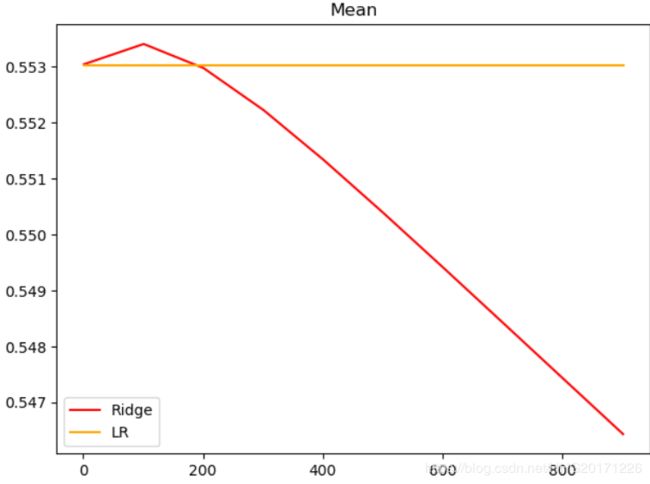
plt.plot(alpharange, ridge, color="red", label="Ridge")
plt.plot(alpharange, lr, color="orange", label="LR")
plt.title("Mean")
plt.legend()
plt.show()

# 模型方差如何变化？
alpharange = np.arange(1, 1001, 100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg, X, y, cv=5, scoring="r2").var()
    varLR = cross_val_score(linear, X, y, cv=5, scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
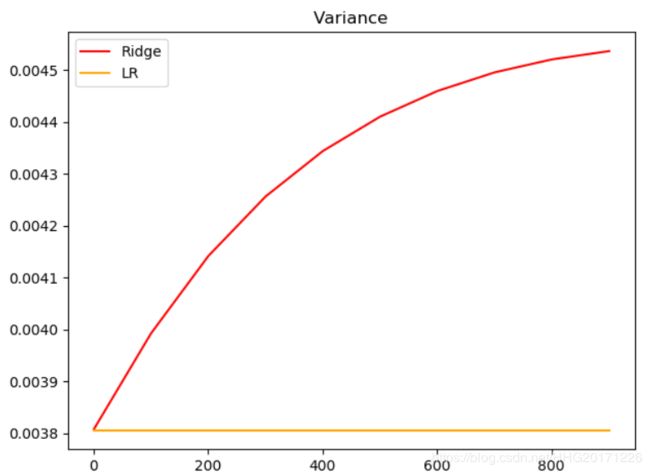
plt.plot(alpharange, ridge, color="red", label="Ridge")
plt.plot(alpharange, lr, color="orange", label="LR")
plt.title("Variance")
plt.legend()
plt.show()

X = load_boston().data
y = load_boston().target

Xtain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=321)

# 查看方差的变化
alpharange = np.arange(1, 1001, 100)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg, X, y, cv=5, scoring="r2").var()
    varLR = cross_val_score(linear, X, y, cv=5, scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
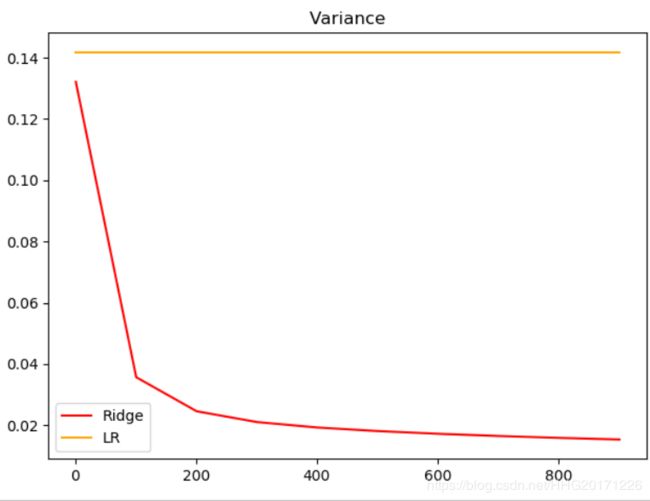
plt.plot(alpharange, ridge, color="red", label="Ridge")
plt.plot(alpharange, lr, color="orange", label="LR")
plt.title("Variance")
plt.legend()
plt.show()

#查看R2的变化
alpharange = np.arange(1,1001,100)
ridge, lr = [], []
for alpha in alpharange:
	reg = Ridge(alpha=alpha)
	linear = LinearRegression()
	regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
	linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
	ridge.append(regs)
	lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

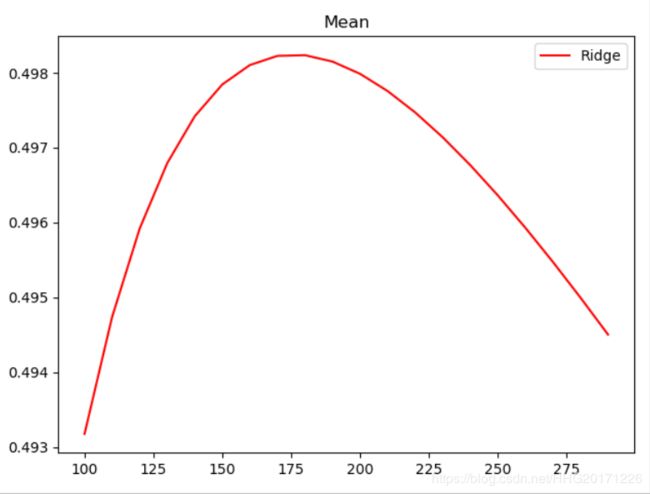
#细化学习曲线
alpharange = np.arange(100,300,10)
ridge, lr = [], []
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    #linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring = "r2").mean()
    #linears = cross_val_score(linear,X,y,cv=5,scoring = "r2").mean()
    ridge.append(regs)
    # lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
#plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

2.3 选取最佳的正则化参数取值

使用交叉验证来选择最佳的正则化系数。在sklearn中，我们有带交叉验证的岭回归可以使用

class sklearn.linear_model.RidgeCV (alphas=(0.1, 1.0, 10.0), 
									fit_intercept=True, 
									normalize=False, 
									scoring=None,
									cv=None, 
									gcv_mode=None, 
									store_cv_values=False
								)

使用我们之前建立的加利佛尼亚房屋价值数据集：

import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing as fch
from sklearn.linear_model import RidgeCV

housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数", "房屋使用年代中位数", "平均房间数目"
    , "平均卧室数目", "街区人口", "平均入住率", "街区的纬度", "街区的经度"]
Ridge_ = RidgeCV(alphas=np.arange(1, 1001, 100)
                 # ,scoring="neg_mean_squared_error"
                 , store_cv_values=True
                 # ,cv=5
                 ).fit(X, y)

# 无关交叉验证的岭回归结果
re = Ridge_.score(X, y)
print(re )
# 调用所有交叉验证的结果
re = Ridge_.cv_values_.shape
print(re )
# 进行平均后可以查看每个正则化系数取值下的交叉验证结果
re = Ridge_.cv_values_.mean(axis=0)
print(re )
# 查看被选择出来的最佳正则化系数
re = Ridge_.alpha_
print(re )

'''
0.6060251767338429
(20640, 10)
[0.52823795 0.52787439 0.52807763 0.52855759 0.52917958 0.52987689
 0.53061486 0.53137481 0.53214638 0.53292369]
101
'''

Lasso

1 Lasso与多重共线性

2 Lasso的核心作用：特征选择

class sklearn.linear_model.Lasso (alpha=1.0, 
									fit_intercept=True, 
									normalize=False, 
									precompute=False,
									copy_X=True, 
									max_iter=1000, 
									tol=0.0001, 
									warm_start=False, 
									positive=False, 
									random_state=None, 
									selection=’cyclic’
								)

lasso如何做特征选择：

import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression, Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt

housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目"
		,"平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
X.head()
Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)

#恢复索引
for i in [Xtrain,Xtest]:
	i.index = range(i.shape[0])

#线性回归进行拟合
reg = LinearRegression().fit(Xtrain,Ytrain)
(reg.coef_*100).tolist()

#岭回归进行拟合
Ridge_ = Ridge(alpha=0).fit(Xtrain,Ytrain)
(Ridge_.coef_*100).tolist()

#Lasso进行拟合
lasso_ = Lasso(alpha=0).fit(Xtrain,Ytrain)
(lasso_.coef_*100).tolist()

#岭回归进行拟合
Ridge_ = Ridge(alpha=0.01).fit(Xtrain,Ytrain)
(Ridge_.coef_*100).tolist()

#Lasso进行拟合
lasso_ = Lasso(alpha=0.01).fit(Xtrain,Ytrain)
(lasso_.coef_*100).tolist()


#加大正则项系数，观察模型的系数发生了什么变化
Ridge_ = Ridge(alpha=10**4).fit(Xtrain,Ytrain)
(Ridge_.coef_*100).tolist()
lasso_ = Lasso(alpha=10**4).fit(Xtrain,Ytrain)
(lasso_.coef_*100).tolist()

#看来10**4对于Lasso来说是一个过于大的取值
lasso_ = Lasso(alpha=1).fit(Xtrain,Ytrain)
(lasso_.coef_*100).tolist()

#将系数进行绘图
plt.plot(range(1,9),(reg.coef_*100).tolist(),color="red",label="LR")
plt.plot(range(1,9),(Ridge_.coef_*100).tolist(),color="orange",label="Ridge")
plt.plot(range(1,9),(lasso_.coef_*100).tolist(),color="k",label="Lasso")
plt.plot(range(1,9),[0]*8,color="grey",linestyle="--")
plt.xlabel('w') #横坐标是每一个特征所对应的系数
plt.legend()
plt.show()

3 选取最佳的正则化参数取值

class sklearn.linear_model.LassoCV (eps=0.001, 
									n_alphas=100, 
									alphas=None, 
									fit_intercept=True,
									normalize=False, 
									precompute=’auto’, 
									max_iter=1000, 
									tol=0.0001, 
									copy_X=True, 
									cv=’warn’, 
									verbose=False,
									n_jobs=None, 
									positive=False, 
									random_state=None, 
									selection=’cyclic’
							)

from sklearn.linear_model import LassoCV

#自己建立Lasso进行alpha选择的范围
alpharange = np.logspace(-10, -2, 200,base=10)

#其实是形成10为底的指数函数
#10**(-10)到10**(-2)次方
alpharange.shape
Xtrain.head()
lasso_ = LassoCV(alphas=alpharange #自行输入的alpha的取值范围
				,cv=5 #交叉验证的折数
				).fit(Xtrain, Ytrain)

#查看被选择出来的最佳正则化系数
lasso_.alpha_

#调用所有交叉验证的结果
lasso_.mse_path_

lasso_.mse_path_.shape #返回每个alpha下的五折交叉验证结果

lasso_.mse_path_.mean(axis=1) #有注意到在岭回归中我们的轴向是axis=0吗？
#在岭回归当中，我们是留一验证，因此我们的交叉验证结果返回的是，每一个样本在每个alpha下的交叉验证结果
#因此我们要求每个alpha下的交叉验证均值，就是axis=0，跨行求均值
#而在这里，我们返回的是，每一个alpha取值下，每一折交叉验证的结果
#因此我们要求每个alpha下的交叉验证均值，就是axis=1，跨列求均值

#最佳正则化系数下获得的模型的系数结果
lasso_.coef_

lasso_.score(Xtest,Ytest)

#与线性回归相比如何？
reg = LinearRegression().fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)

#使用lassoCV自带的正则化路径长度和路径中的alpha个数来自动建立alpha选择的范围
ls_ = LassoCV(  eps=0.00001
				,n_alphas=300
				,cv=5
				).fit(Xtrain, Ytrain)
ls_.alpha_
ls_.alphas_ #查看所有自动生成的alpha取值
ls_.alphas_.shape
ls_.score(Xtest,Ytest)
ls_.coef_

Lasso作为线性回归家族中在改良上走得最远的算法，还有许多领域等待我们去探讨。比如说，在现实中，我们不仅可以适用交叉验证来选择最佳正则化系数，我们也可以使用BIC（ 贝叶斯信息准则）或者AIC（Akaike informationcriterion，艾凯克信息准则）来做模型选择。同时，我们可以不使用坐标下降法，还可以使用最小角度回归来对lasso进行计算。