《算法导论》-读书笔记-第七章-快速排序(QUICKSORT)

序言

快速排序，顾名思义就是具有较快的排序速度，它利用了跟归并排序一样的分治思想。它同时是一种原址性的排序方法，最好情况下的时间复杂度为O(nlgn)， 最坏情况下的时间复杂度为O(n²)。

---

快速排序的描述

快速排序利用的是分治思想，既然用到的是分治思想，那么对于A[p…r]自然就有分解，解决，合并的过程：

分解：数组A[p…r]被划分成两个子数组A[p…q-1]和A[q+1,r],使得A[p…q-1]中的每个元素都小于等于A[q],而A[q]小于等于A[q+1…r]中的元素，下标q也在这个划分过程中进行计算。

解决：通过递归调用快速排序，对子数组A[p…q-1]和A[q+1…r]排序

合并：由于快排具有原址性，所以是不需要合并的。

对于快速排序的过程，在书中的源代码是：

 QUICKSORT(A,p,r)
     if p > r
         then q = PARTITION(A,p,r)
         QUICKSORT(A,p,q-1)
         QUICKSORT(A,q+1,r)

可以看出快排和前面章节介绍的归并排序在算法上具有一定的相似性。主要的关键步骤在于PARTITION函数，返回值是关键字的位置q。

对于数组的划分（PARTITION），在书中的源代码是：

PARTITION(A,p,r)
     x = A[r]
     i = p-1
     for j = p to r-1
         do if A[j] ≤ x
             then i ++
                   swap(A[i],A[j])
     swap(A[i+1],A[r])
     return i+1

选取最后一个数作为基准数，经过这样的一趟划分下来后，会使得A[q]的左边的数都小于A[q]，A[q]的右边的数都大于A[q]， 而A[q]恰好是这个基准数。具体过程如下图：

快速排序算法的C语言实现

根据书中的源代码，很容易用C语言写出：

#include 

void QuickSort(int* A, int p, int r);  //快速排序
int Partition(int* A, int p, int r);   //数组的划分
void swap(int* a, int* b);             //两数交换

void main()
{
	int Array[8] = { 6,2,4,3,8,9,7,1 };
	int p = 0;
	int r = 7;
	QuickSort(Array, p, r);

	for (int k = 0; k < 8; k++)
		printf("%d ", Array[k]);
	printf("\n");
}

void QuickSort(int* A, int p, int r)    //快速排序
{
	int q;

	if (p < r)
	{
		q = Partition(A, p, r);
		QuickSort(A, p, q - 1);        //递归调用
		QuickSort(A, q + 1, r);
	}
}

int Partition(int* A, int p, int r)   //实现数组的划分
{
	int x, i, j, temp;

	x = A[r];                        //取最后一个数作为基准数
	i = p - 1;
	for (j = p; j < r; j++) {
		if (A[j] <= x)
		{
			i++;
			swap(&A[i], &A[j]);
		}
	}
	swap(&A[i + 1], &A[r]);
	return i + 1;
}

void swap(int* a, int* b) {      //交换a,b两个数
	int temp;

	temp = *a;
	*a = *b;
	*b = temp;
}

快速排序的性能分析

快速排序的运行时间依赖于划分是否平衡，平衡与否有依赖于划分的元素。如果划分是平衡的，快排的性能会和归并排序是一样的，如果不平衡的话，那么快排就会接近于插入算法。

• 最坏情况划分
  在快排中，最坏的情况就是说对已经排好序的数组进行排序。他的递归式是T(N) = T(N-1)+T(0)+O(N)。根据这个表达式我们可以得出所需要的时间是O(n²)

• 最好情况划分
  平衡的划分使得PARTITION过程得到的两个子序列。这两个子序列的规模都不超过n/2，这种情况下快排的性能是非常好的。他的递归式为：T(N) = 2T(N/2) + O(N),由主方法可以得出，他的时间为：Θ(nlgn)。

• 平衡的划分
  快速排序的平均情况运行时间与其最佳情况运行时间很接近，而不是非常接近于其最坏情况运行时间。例如：假设划分过程总是产生9:1的划分，算法的运行时间可表示为：T(N) <= T(9N/10)+T(N/10)+cn。这一递归式对应的递归树如图：
  
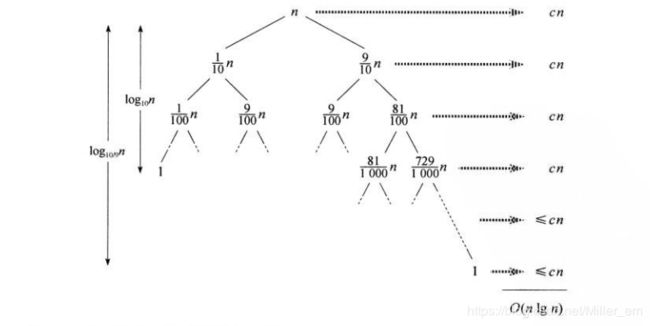
  在递归的每一层上都是9: 1的划分，直观上看起来非常不平衡，但快速排序的运行时间是O(nlgn)，与恰好在中间划分的渐近运行时间是一样的。实际上，即使是99 : 1的划分，其时间复杂度仍然是O(nlgn)。事实上，任何一种常数比例的划分都会产生深度为Θ(lgn)的递归树，其中每一-层的时间代价都是O(n)。因此，只要划分是常数比例的，算法的运行时间总是O(nlgn)。