探索性数据分析:自然断点法算法原理及Python实现
虽然这是2020年第一篇,不过根据我兔的习惯,俺们通常是过农历大年才算过年,所以这篇依然算是旧历年的文章,不算开篇制作。
在做专题制图的时候,需要把专题数据分成若干类别,分类的标准当然仁者见仁智者见智,比如我以前写过的分位数分级法,就是一种极好的方法:
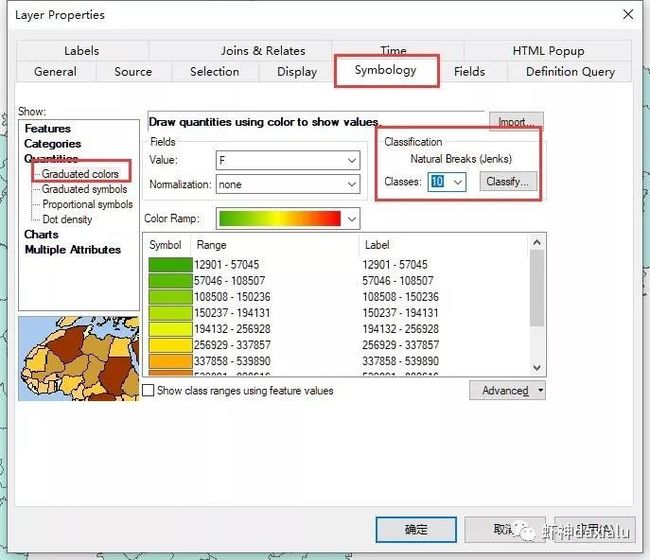
但是分位数分级法限定就是六类(不算缺失值),如果需要更多的类别,就不适用了,而在ArcGIS里面,提供了一种非常好用,也是最常用的分类方法,就是所谓的自然断点法:
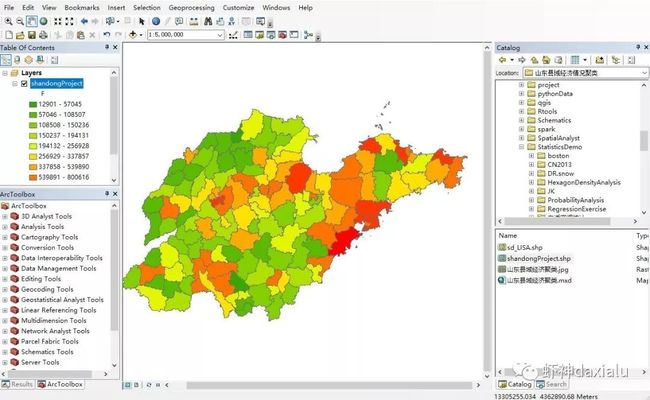
比如我把山东省各县的GDP划分成10个等级:
自然断点法可以根据你选择的级别进行划分,是最省时省力的方法。
既然自然断点这个方法这么好用,我如果脱离ArcGIS,用在其他地方呢?是否有办法?答案当然是肯定的,下面我们来介绍一下,自然断点法的原理在Python可视化里面的应用。
自然断点法运用了聚类的思维,它的核心思想与聚类一样:使每一组内部的相似性最大,而外部组与组之间的相异性最大。但是与聚类不一样的地方,聚类是不会关注每一类中的要素数量和范围的,而自然断点法在于它还会兼顾每一组之间的要素的范围和个数尽量相近。
自然断点法有两个称呼,一个就是直接英文名称,叫做“Natural Breaks”,这就不解释了,还有一个称呼就是ArcGIS里面用的,叫做“Jenks”,主要是来源于它的创造者:乔治·弗雷德里克·詹克斯(George Frederick Jenks)教授:
乔治·弗雷德里克·詹克斯教授
(George Frederick Jenks)
(1916-1996),
1916年7月9日出生在纽约,
1950年在锡拉丘兹大学获得了地理学博士学位,
第二次世界大战的时候,作为测绘和制图师,詹克斯为美国空军工作;
在他的职业生涯中,专注于制图学,是美国最著名的制图学家之一。
他从1949年开始执教于美国堪萨斯大学地理系,
并且创立了该校制图专业,于1986年从堪萨斯大学退休。
詹克斯博士于1996年12月去世,享年80岁。
自然断点法的意义在于,詹克斯教授认为任何数列之间,都存在一些自然(非人为设定的)的转折点和断点,这些自然的断点,都是具有统计学意义的,用这些转折点可以把研究的对象分成性质相似的群组,因此,自然断点本身就是分级的良好界限。
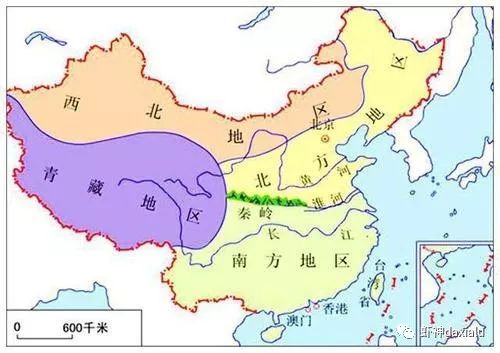
正如地理上一样,大部分自然的分界线效果都非常好,比如中国的南北分界线:秦岭——淮河:
当然, 如果是人为来分,就不是这样了,比如对于广东人来说:
那么如何来寻找这些断点呢?他设计了一种算法,通过迭代比较每个分组和分组中元素的均值与观测值之间的平方差之和来确定值在分组中的最佳排列。计算出来的最佳分类,可确定值在有序分布中的中断点,以最大程度地减少组内平方差之和。
好吧,上面这个说法比较晦涩,下面通过一个简单的算法,来给大家说明一下自然断点法的原理:
比如我们现在有四个值:4,5,9,10,要分成两类
我信你鬼,不用算,都能看出来,
4,5一类,9,10一类)、:
稍安勿躁,我们来看看在自然断点法里面应该如何计算呢:
第一步:计算数组“平均值的偏差平方和”(SDAM),算法如下:
计算平均值:
(4+5+9+10)/4= 7
计算SDAM
(4-7)^ 2 +(5-7)^ 2 +(9-7)^ 2 +(10-7) ^ 2
= 9 + 4 + 4 + 9 =26
第二步,迭代每个范围组合,计算“类别均值的平方偏差平方和”(SDCM_ALL),然后找到最小的:
第一组:[4] [5,9,10],
SDCM_ALL
=(4-4)^ 2 +(5-8)^ 2 +(9-8)^ 2 +(10-8)^ 2
= 0 + 9 + 1 + 4 =14。
第二组:[4,5] [9,10],
SDCM_ALL
=(4-4.5)^ 2 +(5-4.5)^ 2 +(9-9.5)^ 2 +(10-9.5)^ 2
= 0.25 + 0.25 + 0.25 + 0.25 =1。
第三组:[4,5,9] [10],
SDCM_ALL
=(4-6)^ 2 +(5-6)^ 2 +(9-6)^ 2 + (10-10)^ 2
= 4 +1 + 9 + 0 =14。
实际上这样已经能够看出来最小的肯定就是第二组分类方法了,但是詹克斯教授还设计了第三步,也就是对数值进行汇总度量:
第三步,计算“方差拟合优度”(GVF)
GVF= (SDAM-SCDM)/ SDAM
GVF的值是在0-1之间,1表示拟合极好,0表示拟合极差,算法如下:
第二组计算结果为:(26-1)/ 26 = 25/26 = 0.9
其他两组计算结果为:(26-14)/ 26 = 12/26 = 0.46
在这个算法被发明很长时间内,都被视为少量数据集的最佳划分方法,但是因为采用迭代组合来进行计算,被认为不适用于大型数据集——直到计算机被广泛应用在各行各业中。
上面简单介绍了一下自然断点法的计算原理,不过没有打算让大家自己去写一个实现,因为重复造轮子这种事,是木有意义,下面我们来介绍Python里面来实现自然断点法的包:jenkspy
地址:https://pypi.org/project/jenkspy/
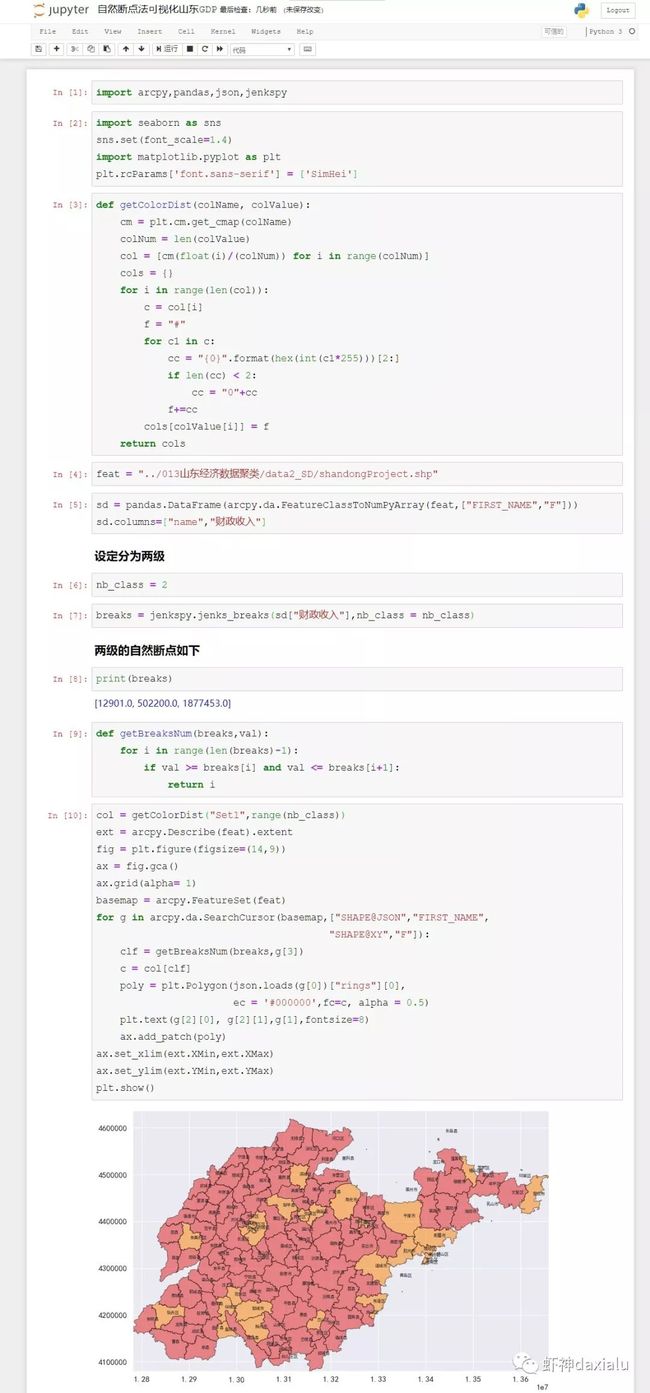
安装和使用都非常简单,安装的话,直接pip就可以了,使用的话,也非常简单,看下面的Demo:
打完收工,源代码在老地方找:
https://github.com/allenlu2008/PythonDemo
018自然断点法,数据用的013,山东经济聚类的数据。