深度学习与卷积神经网络--识别鸟

作者：Adam Geitgey

原文：https://medium.com/@ageitgey/machine-learning-is-fun-part-3-deep-learning-and-convolutional-neural-networks-f40359318721#.3n9dohehj

译者：巡洋舰科技——赵95

校对：离线Offline——林沁

转载请联系译者。

你是不是看烦了各种各样有关深度学习的报道，却仍不知其所云？让我们一起来改变这个现状吧！

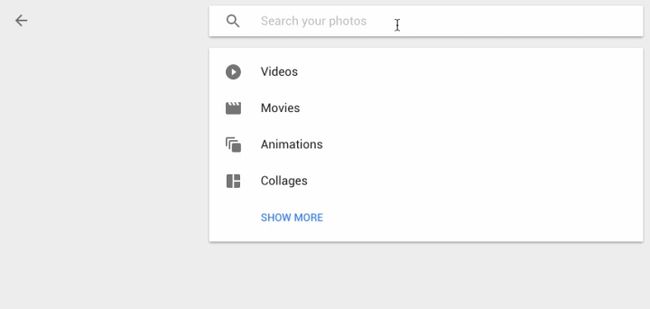
这一次，我们将应用深度学习技术，来写一个识别图像中物体的程序。换句话说，我们会解释 Google 相册搜索图片时所用到的「黑科技」：

Google 现在可以让你在你自己的图片库里面，根据你的描述搜索图片，即使这些图片根本没有被标注任何标签！这是怎么做到的？？

和第一、二章一样，这篇指南是为那些对机器学习感兴趣，但又不知从哪里开始的人而写的。这意味着文中有大量的概括。但是那又如何呢？只要能让读者对机器学习更感兴趣，这篇文章的任务也就完成了。

用深度学习识别物体

xkcd#1425（出自http://xkcd.com，汉化来自http://xkcd.tw）

你可能曾经看过这个著名的 xkcd 的漫画。

一个 3 岁的小孩可以识别出鸟类的照片，然而最顶尖的计算机科学家们已经花了 50 年时间来研究如何让电脑识别出不同的物体。漫画里的灵感就是这么来的。

在最近的几年里，我们终于找到了一种通过深度卷积神经网络（deep convolutional neural networks）来进行物体识别的好方法。这些个词听起来就像是威廉·吉布森科幻小说里的生造词，但是如果你把这个想法逐步分解，你绝对可以理解它。

让我们开始吧——让我们一起来写一个识别鸟类的程序！

由浅入深

在我们在识别鸟类之前，让我们先做个更简单的任务——识别手写的数字「8」。

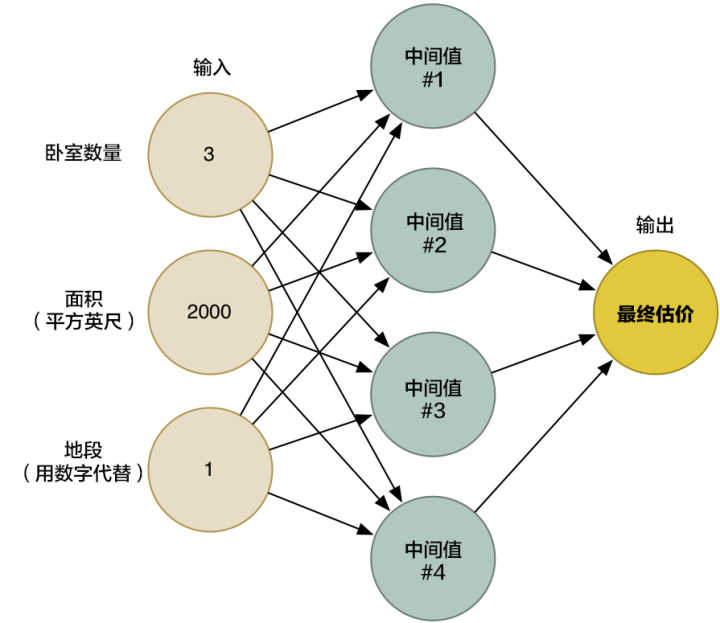
在第二章中，我们已经了解到神经网络是如何通过连接无数神经元来解决复杂问题的。我们创造了一个小型神经网络，然后根据各种因素（房屋面积、格局、地段等）来估计房屋的价格：

在第一章中我们提到了，机器学习，就是关于重复使用同样的泛型算法，来处理不同的数据，解决不同的问题的一种概念。所以这次，我们稍微修改一下同样的神经网络，试着用它来识别手写文字。但是为了更加简便，我们只会尝试去识别数字「8」。

机器学习只有在你拥有数据（最好是大量数据）的情况下，才能有效。所以，我们需要有大量的手写「8」来开始我们的尝试。幸运的是，恰好有研究人员建立了 MNIST 手写数字数据库，它能助我们一臂之力。MNIST提供了 60,000 张手写数字的图片，每张图片分辨率为 18×18。下列是数据库中的一些例子：

MNIST数据库中的数字「8」

万物皆「数」

在第二章中我们创造的那个神经网络，只能接受三个数字输入（卧室数、面积、地段）。但是现在，我们需要用神经网络来处理图像。所以到底怎样才能把图片，而不是数字，输入到神经网络里呢？

结论其实极其简单。神经网络会把数字当成输入，而对于电脑来说，图片其实恰好就是一连串代表着每个像素颜色的数字：

我们把一幅 18×18 像素的图片当成一串含有 324 个数字的数组，就可以把它输入到我们的神经网络里面了：

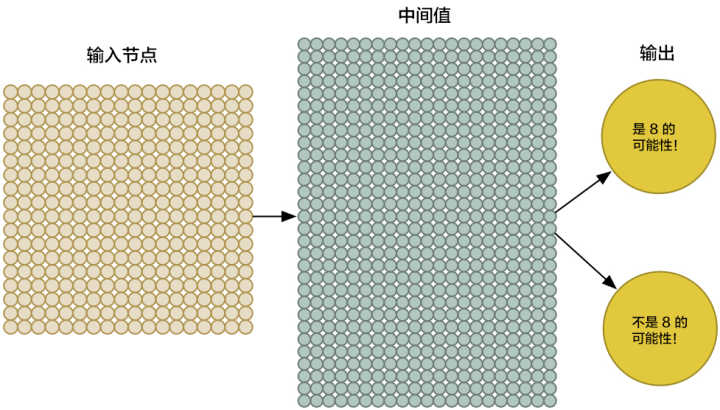
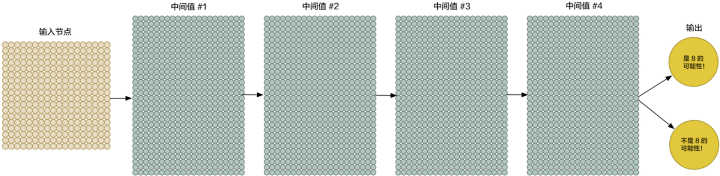
为了更好地操控我们的输入数据，我们把神经网络的输入节点扩大到 324 个：

请注意，我们的神经网络现在有了两个输出（而不仅仅是一个房子的价格）。第一个输出会预测图片是「8」的概率，而第二个则输出不是「8」的概率。概括地说，我们就可以依靠多种不同的输出，利用神经网络把要识别的物品进行分组。

虽然我们的神经网络要比上次大得多（这次有 324 个输入，上次只有 3 个！），但是现在的计算机一眨眼的功夫就能够对这几百个节点进行运算。当然，你的手机也可以做到。

现在唯一要做的就是用各种「8」和非「8」的图片来训练我们的神经网络了。当我们喂给神经网络一个「8」的时候，我们会告诉它是「8」的概率是 100% ，而不是「8」的概率是 0%，反之亦然。

下面是一些训练数据：

嗯……训练数据好好吃

在现代的笔记本电脑上，训练这种神经网络几分钟就能完成。完成之后，我们就可以得到一个能比较准确识别字迹「8」的神经网络。欢迎来到（上世纪八十年代末的）图像识别的世界！

短浅的目光

仅仅把像素输入到神经网络里，就可以识别图像，这很棒！机器学习就像魔法一样！……对不对？

呵呵，当然，不会，这么，简单。

首先，好消息是，当我们的数字就在图片的正中间的时候，我们的识别器干得还不错。

坏消息是:

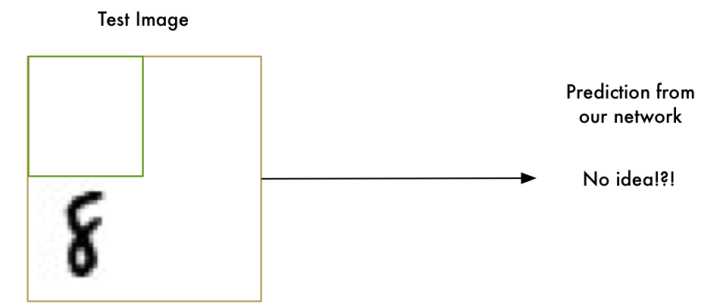
当数字并不是正好在图片中央的时候，我们的识别器就完全不工作了。一点点的位移我们的识别器就掀桌子不干了(╯‵□′)╯︵┻━┻。

这是因为我们的网络只学习到了正中央的「8」。它并不知道那些偏离中心的「8」长什么样子。它仅仅知道中间是「8」的图片规律。

在真实世界中，这种识别器好像并没什么卵用。真实世界的问题永远不会如此轻松简单。所以，我们需要知道，当「8」不在图片正中时，怎么才能让我们的神经网络识别它。

暴力方法 #1：滑框搜索

我们已经创造出了一个能够很好地识别图片正中间「8」的程序。如果我们干脆把整个图片分成一个个小部分，并挨个都识别一遍，直到我们找到「8」，这样能不能行呢？

这个叫做滑动窗口算法（sliding window），是暴力算法之一。在有限的情况下，它能够识别得很好。但实际上它并不怎么有效率，你必须在同一张图片里面一遍一遍地识别不同大小的物体。实际上，我们可以做得更好！

暴力方法 #2：更多的数据与一个深度神经网

刚刚我们提到，经过训练之后，我们只能找出在中间的「8」。如果我们用更多的数据来训练，数据中包括各种不同位置和大小的「8」，会怎样呢？

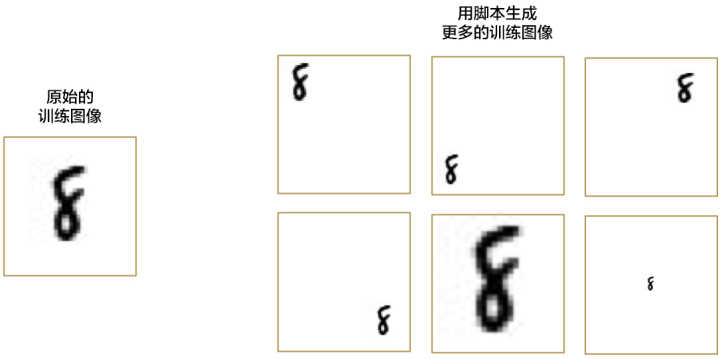
我们并不需要收集更多的训练数据。实际上，我们可以写一个小脚本来生成各种各样不同位置「8」的新图片：

通过组合不同版本的训练图片，我们创造出了合成训练数据（Synthetic Training Data）。这是一种非常实用的技巧！

使用这种方法，我们能够轻易地创造出无限量的训练数据。

数据越多，这个问题对神经网络来说就越复杂。但是通过扩大神经网络，它就能寻找到更复杂的规律了。

要扩大我们的网络，我们首先要把把节点一层一层的堆积起来：

因为它比传统的神经网络层数更多，所以我们把它称作「深度神经网络」（deep neural network）。

这个想法在二十世纪六十年代末就出现了，但直至今日，训练这样一个大型神经网络也是一件缓慢到不切实际的事情。然而，一旦我们知道了如何使用 3D 显卡（最开始是用来进行快速矩阵乘法运算）来替代普通的电脑处理器，使用大型神经网络的想法就立刻变得可行了。实际上，你用来玩守望先锋的 NVIDIA GeForce GTX1080 这款显卡，就可以极快速的训练我们的神经网络。

但是尽管我们能把我们的神经网络扩张得特别大，并使用 3D 显卡快速训练它，这依然不能让我们一次性得到结论。我们需要更智能地将图片处理后，放入到神经网络里。

仔细想想，如果把图片最上方和最下方的「8」当成两个不同的对象来处理，并写两个不同的网络来识别它们，这件事实在是说不通。

应该有某种方法，使得我们的神经网络，在没有额外的训练数据的基础上，能够非常智能的识别出图片上任何位置的「8」，都是一样是「8」。幸运的是……这就是！

卷积性的解决办法

作为人类，你能够直观地感知到图片中存在某种层级（hierarchy）或者是概念结构（conceptual structure）。参考下面的这个图片：

作为人类，你立刻就能识别出这个图片的层级：

· 地面是由草和水泥组成的

· 图中有一个小孩

· 小孩在骑弹簧木马

· 弹簧木马在草地上

最重要的是，我们识别出了小孩儿，无论这个小孩所处的环境是怎样的。当每一次出现不同的环境时，我们人类不需要重新学习小孩儿这个概念。

但是现在，我们的神经网络做不到这些。它认为「8」出现在图片的不同位置，就是不一样的东西。它不能理解「物体出现在图片的不同位置还是同一个物体」这个概念。这意味着在每种可能出现的位置上，它必须重新学习识别各种物体。这弱爆了。

我们需要让我们的神经网络理解平移不变性（translation invariance）这个概念——也就是说，无论「8」出现在图片的哪里，它都是「8」。

我们会通过一个叫做卷积（Convolution）的方法来达成这个目标。卷积的灵感是由计算机科学和生物学共同激发的。（有一些疯狂的生物学家，它们用奇怪的针头去戳猫的大脑，来观察猫是怎样处理图像的 >_<）。

卷积是如何工作的

之前我们提到过，我们可以把一整张图片当做一串数字输入到神经网络里面。不同的是，这次我们会利用「位移物相同」[1]的概念来把这件事做得更智能。

下面就是，它怎样工作的分步解释——

第一步：把图片分解成部分重合的小图块

和上述的滑框搜索类似的，让我们把滑框滑过整个图片，并存储下每一个框里面的小图块：

这么做之后，我们把图片分解成了 77 块同样大小的小图块。

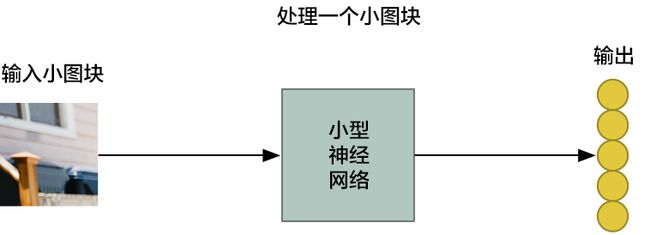
第二步：把每个小图块输入到小型神经网络中

之前，我们做的事是把单张图片输入到神经网络中，来判断它是否一为「8」。这一次我们还做同样的事情，只不过我们输入的是一个个小图块：

重复这个步骤 77 次，每次判断一张小图块。

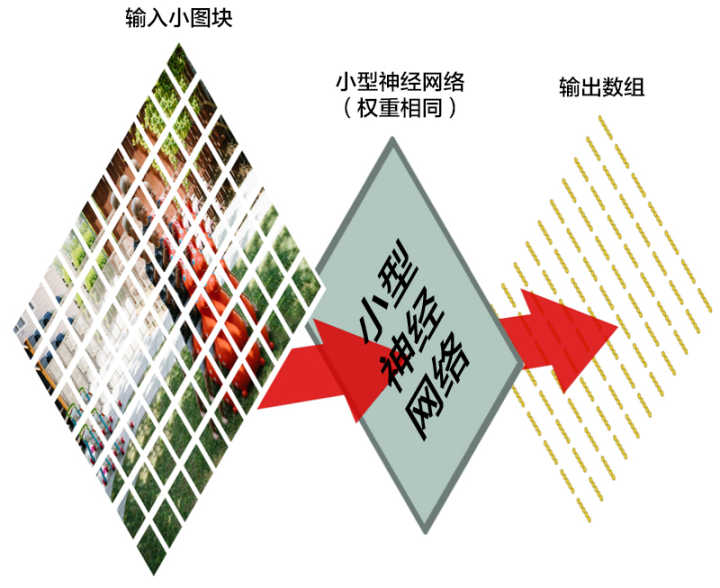
然而，有一个非常重要的不同：对于每个小图块，我们会使用同样的神经网络权重。换一句话来说，我们平等对待每一个小图块。如果哪个小图块有任何异常出现，我们就认为这个图块是「异常」（interesting）的

第三步：把每一个小图块的结果都保存到一个新的数组当中

我们不想并不想打乱小图块的顺序。所以，我们把每个小图块按照图片上的顺序输入并保存结果，就像这样：

换一句话来说，我们从一整张图片开始，最后得到一个稍小一点的数组，里面存储着我们图片中的哪一部分有异常。

第四步：缩减像素采样

第三步的结果是一个数组，这个数组对应着原始图片中最异常的部分。但是这个数组依然很大:

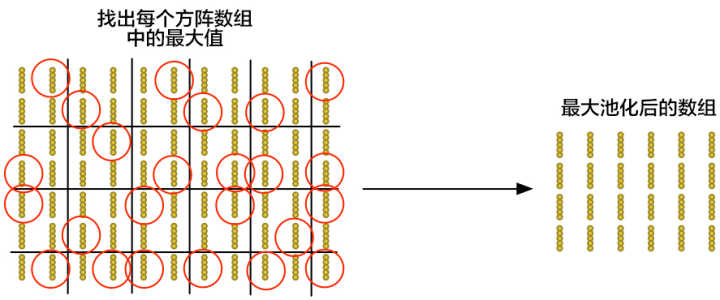
为了减小这个数组的大小，我们利用一种叫做最大池化（max pooling）的函数来降采样（downsample）。它听起来很棒，但这仍旧不够！

让我们先来看每个 2×2 的方阵数组，并且留下最大的数：

这里，一旦我们找到组成 2×2 方阵的 4 个输入中任何异常的部分，我们就只保留这一个数。这样一来我们的数组大小就缩减了，同时最重要的部分也保留住了。

最后一步：作出预测

到现在为止，我们已经把一个很大的图片缩减到了一个相对较小的数组。

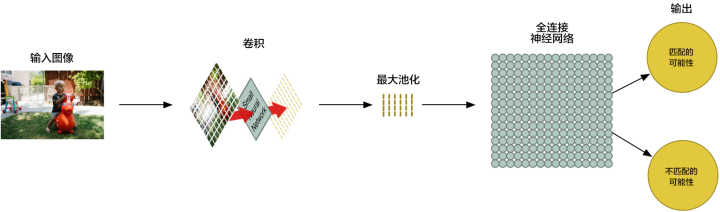
你猜怎么着？数组就是一串数字而已，所以我们我们可以把这个数组输入到另外一个神经网络里面去。最后的这个神经网络会决定这个图片是否匹配。为了区分它和卷积的不同，我们把它称作「全连接」网络（“Fully Connected” Network）。

所以从开始到结束，我们的五步就像管道一样被连接了起来：

添加更多步骤

我们的图片处理管道是一系列的步骤：卷积、最大池化，还有最后的「全连接」网络。

你可以把这些步骤任意组合、堆叠多次，来解决真实世界中的问题！你可以有两层、三层甚至十层卷积层。当你想要缩小你的数据大小时，你也随时可以调用最大池化函数。

我们解决问题的基本方法，就是从一整个图片开始，一步一步逐渐地分解它，直到你找到了一个单一的结论。你的卷积层越多，你的网络就越能识别出复杂的特征。

比如说，第一个卷积的步骤可能就是尝试去识别尖锐的东西，而第二个卷积步骤则是通过找到的尖锐物体来找鸟类的喙，最后一步是通过鸟喙来识别整只鸟，以此类推。

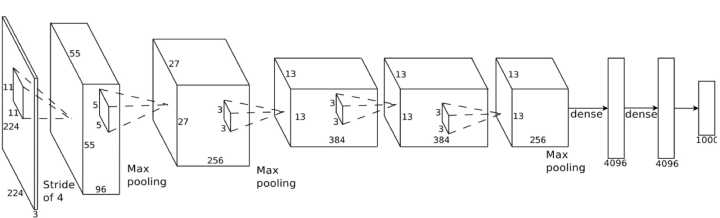
下面是一个更实际的深层卷积网络的样子（就是你们能在研究报告里面找到的那种例子一样）：

这里，他们从一个 224×224 像素的图片开始，先使用了两次卷积和最大池化，再使用三次卷积，一次最大池化；最后再使用两个全连接层。最终的结果是这个图片能被分类到 1000 种不同类别当中的某一种！

建造正确的网络

所以，你是怎么知道我们需要结合哪些步骤来让我们的图片分类器工作呢？

说句良心话，你必须做许多的实验和检测才能回答这个问题。在为你要解决的问题找到完美的结构和参数之前，你可能需要训练 100 个网络。机器学习需要反复试验！

建立我们的鸟类分类器

现在我们已经做够了准备，我们已经可以写一个小程序来判定一个图中的物体是不是一只鸟了。

诚然，我们需要数据来开始。CIFAR10 数据库免费提供了 6000 张鸟类的图片和 52000 张非鸟类的图片。但是为了获取更多的数据，我们仍需添加 Caltech-UCSD Birds-200-2011 数据库，这里面包括了另外的 12000 张鸟类的图片。

这是我们整合后的数据库里面的一些鸟类的图片：

这是数据库里一些非鸟类图片：

这些数据对于我们这篇文章解释说明的目的来说已经够了，但是对于真实世界的问题来说，72000 张低分辨率的图片还是太少了。如果你想要达到 Google 这种等级的表现的话，你需要上百万张高清无码大图。在机器学习这个领域中，有更多的数据永远比一个更好的算法更重要！现在你知道为什么谷歌总是乐于给你提供无限量免费图片存储了吧？ 他们，需要，你的，数据！

为了建立我们的分类器，我们将会使用 TFLearn。TFLearn 是 Google TensorFlow 的一个封装，Google TensorFlow 包含了一个拥有简单 API 的深度学习库。用它来建立卷积网络的过程，和写几行代码定义我们网络的层级一样简单。

下面是定义并训练我们网络的代码：

# -*- coding: utf-8 -*-



"""



基于这个 tflearn 样例代码:



https://github.com/tflearn/tflearn/blob/master/examples/images/convnet_cifar10.py



"""



from __future__ import division, print_function,
absolute_import



# 导入 tflearn 和一些辅助文件



import tflearn



from tflearn.data_utils import shuffle



from tflearn.layers.core import input_data,
dropout, fully_connected



from tflearn.layers.conv import conv_2d,
max_pool_2d



from tflearn.layers.estimator import regression



from tflearn.data_preprocessing import
ImagePreprocessing



from tflearn.data_augmentation import
ImageAugmentation



import pickle



# 加载数据集



X, Y, X_test, Y_test =
pickle.load(open("full_dataset.pkl", "rb"))



# 打乱数据



X, Y = shuffle(X, Y)



# 确定数据是规范的



img_prep = ImagePreprocessing()



img_prep.add_featurewise_zero_center()



img_prep.add_featurewise_stdnorm()



# 翻转、旋转和模糊效果数据集中的图片,



# 来创造一些合成训练数据.



img_aug = ImageAugmentation()



img_aug.add_random_flip_leftright()



img_aug.add_random_rotation(max_angle=25.)



img_aug.add_random_blur(sigma_max=3.)



# 定义我们的网络架构:



# 输入内容是一张 32x32 大小, 3 个颜色通道(红、绿、蓝）的图片



network = input_data(shape=[None, 32, 32, 3],



            
        data_preprocessing=img_prep,



            
        data_augmentation=img_aug)



# 第一步: 卷积



network = conv_2d(network, 32, 3,
activation='relu')



# 第二步: 最大池化



network = max_pool_2d(network, 2)



# 第三步: 再卷积



network = conv_2d(network, 64, 3,
activation='relu')



# 第四步: 再再卷积



network = conv_2d(network, 64, 3,
activation='relu')



# 第五步: 再最大池化



network = max_pool_2d(network, 2)



# 第六步: 拥有 512 个节点的全连接神经网络



network = fully_connected(network, 512,
activation='relu')



# 第七步: Dropout - 在训练过程中随机丢掉一些数据来防止过拟合



network = dropout(network, 0.5)



# 第八步: 拥有两个输出 (0=不是鸟, 1=是鸟) 的全连接神经网络，yong l做出最终预测



network = fully_connected(network, 2,
activation='softmax')



# 告诉 tflearn 我们想如何训练神经网络



network = regression(network, optimizer='adam',



            
        loss='categorical_crossentropy',



            
        learning_rate=0.001)



# 把网络打包为一个模型对象  



model = tflearn.DNN(network,
tensorboard_verbose=0, checkpoint_path='bird-classifier.tfl.ckpt')



# 开始训练！我们将进行 100 次训练, 并实时监视它.



model.fit(X, Y, n_epoch=100, shuffle=True,
validation_set=(X_test, Y_test),



        
 show_metric=True, batch_size=96,



        
 snapshot_epoch=True,



        
 run_id='bird-classifier')



# 当训练结束时保存模型



model.save("bird-classifier.tfl")



print("Network trained and saved as
bird-classifier.tfl!")

如果你的游戏显卡足够好，显存足够大（比如说 Nvidia GeForce GTX980 Ti），一个小时以内训练就能结束，但是如果你用一般的 CPU 来训练的话，需要的时间可能更长。

随着训练的进行，准确度也会增加。在第一遍训练之后，它的准确率是75.4%。10 次训练之后，准确率就上升到了 91.7%。当训练了大约 50 次的时候，它的准确率达到了 95.5%。继续训练并没有增加它的准确度，所以我停止了。

恭喜！我们的程序现在能识别鸟类的图片了！

测试我们的网络

现在我们拥有了一个训练过的神经网络，我们可以开始使用它了！这儿有一个简单的脚本，能够接收一个图片并预测图中是否是鸟类。

但是为了真正检测我们的神经网络的效果，我们需要大量的图片来测试。我创造的那个数据库里面有 15000 张用来验证的图片。当我把这 15000 张图片放到程序里运行的时候，它的预测准确率达到了 95%。

看起来还不错，对吧？呃……这事儿吧还得辩证地看……

95% 是有多准确？

我们的网络声称有 95% 的准确率。但是细节决定成败，这个数字的表示的意义可能有很多。

比如说，如果我们的训练图片是由 5% 的鸟类图片和 95% 的非鸟类图片组成的呢？一个程序即使每次都猜「不是鸟」也能达到 95% 的准确率！这也就意味着这个程序并没有什么作用。

相比于准确率，我们必须更多地关注在数字本身。为了判别一个分类系统有多好，我们需要知道它是怎样出错误的，而不是仅仅关注它错了多少次。

与其只考虑我们预测的对与错，不如把我们的程序分解成四个不同的类别——

· 首先，对于那些被我们的网络正确辨认为鸟类而且确实是鸟类的，我们叫他们真正类（True Positives）：

哇哦！我们的网络能够识别那么多种不同的鸟类！

· 第二，被辨认为非鸟类，而且确实是非鸟类的，我们称为真负类（True Negatives）：

我们才不会认错马和卡车呢！

· 第三，被辨认为鸟类，但实际上却是非鸟类的，我们叫假正类（False Positives）：

好多飞机被误认成了鸟！情有可原。

· 第四，被辨认为非鸟类，但却是鸟类的，我们叫假负类（False Negatives）：

这些鸟骗过我们！蠢蠢的鸵鸟！它们能算是鸟类吗？

那 15000 张验证图片中，每种类别的数量如下图所示：

为什么我们要把结果做上述分类呢？因为每一个错误产生的几率并不都是一样的。

设想如果我们写一个通过 MRI 图像来探测癌症的程序。如果我们探测到了癌症，我们更希望它是假正类而不是假负类。因为假负类是最可怕的情况——那就是你的程序告诉你，你绝对没有病，但实际上你已经病入膏肓了。

我们需要计算准确率和召回率（Precision and Recall metrics）而并不仅仅关注总体的准确度。准确率和召回率给了我们程序表现的一个清晰的反馈：

这告诉我们，在我们判定是「鸟类」的样本中，有 97% 的样本的确是鸟类！但是这同时也告诉我们说，我们只找出了整个数据集中 90% 的真实鸟类。换句话说，我们可能不会找到每一只鸟，但是当我们找到一只鸟的时候，我们很确定它就是一只鸟！

路还在远方……

现在既然你知道了一些关于深度卷积网络的基本概念，你可以用 TFLearn 尝试一下各种结构神经网络的例子。它包括了自带的数据集，你甚至不用自己去收集图片。

你同时也知道了如何开始创造分支或是学习机器学习的其他领域。接下来为什么不尝试着去学习如何用算法来训练我们的电脑玩雅达利的游戏呢？

1. 译者注：也就是平移不变性。