matlab学习
###技能学习记录:
####matlab的应用:
plot画函数:
plot(y)
plot(x,y)
x=linspace(0,2*pi,30); % 生成一组线性等距的数值
y=sin(x);
plot(x,y) %生成的图形是上30个点连成的光滑的正弦曲线。
x=0:pi/15:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2) %在一张图中画两条正弦曲线
另一种画法是利用hold命令。在已经画好的图形上,
若设置hold on,MATLA将把新的plot命令产生的图形画在原来的图形上。
而命令hold off 将结束这个过程
grid %网格
xlabel(‘Independent Variable X’)%x轴标记
ylabel(‘Dependent Variables Y and Z’)%y轴标记
title(‘Sine and Cosine Curves’)%标题
线型和颜色:
线型 线方式: - 实线 :点线 -. 虚点线 - - 波折线
线型 点方式: . 圆点 +加号 * 星号 x x形 o 小圆
颜色: y黄; r红; g绿; b蓝; w白; k黑; m紫; c青.
坐标系的控制:
在缺省情况下MATLAB自动选择图形的横、纵坐标的比例,如果你对这个比例不满意,可以用axis命令控制
axis([xmin xmax ymin ymax])
axis equal 或 axis(‘equal’) x轴和y轴的单位长度相同
axis square 或 axis(‘square’) 图框呈方形
axis off 或 axis(‘off’) 清除坐标刻度
多幅图形:
可以在同一个画面上建立几个坐标系, 用subplot(m,n,p)命令;把一个画面分成m×n个图形区域, p代表当前的区域号,在每个区域中分别画一个图,如
x=linspace(0,2*pi,30); y=sin(x); z=cos(x);
u=2*sin(x).*cos(x); v=sin(x)./cos(x);
subplot(2,2,1),plot(x,y),axis([0 2*pi –1 1]),title(‘sin(x)’)
subplot(2,2,2),plot(x,z),axis([0 2*pi –1 1]),title(‘cos(x)’)
subplot(2,2,3),plot(x,u),axis([0 2*pi –1 1]),title(‘2sin(x)cos(x)’)
subplot(2,2,4),plot(x,v),axis([0 2*pi –20 20]),title(‘sin(x)/cos(x)’)
画二维矩阵的3维展示:
图片读取:
imgsrc=imread('imgpath');
imggray=rgb2gray(imgsrc);
图像展示及命名:
figure('Name','imgsrc');
figure('position',[200,200,500,500]) 指定窗口位置[left,bottom,width,height]
RGB转Gray:
创建矩阵:
图像灰度x方向投影:
img_x=sum(f,2)/n;
plot(img_x,'r','LineWidth',1.5); %以序号为横坐标,img_x的值为纵坐标画出的折线
图像灰度y方向投影:
img_y=sum(f,1)/m;
plot(img_y,'r','LineWidth',1.5);
图像二值化:
thresh=graythresh(img);%OTSU算法
B=im2bw(A,thresh);%对图像二值化
大津法:
1、计算每个灰度值的概率并计算目标和背景的分布概率以及平均灰度值和方差。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ybWEcIk1-1575685717210)(/media/hhg/EWorkData/WebPictures/LearnSkill/20161124214056127.jpeg)]//显示本地图片
图片//加!可以显示出来
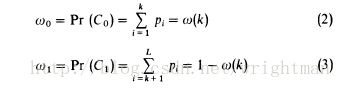
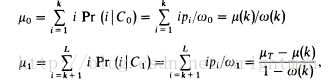
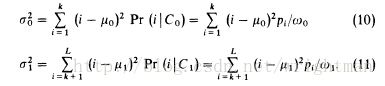
2、计算类间差
3、取类间差最大的灰度值即为阈值
graythresh(image)函数输入是一副图像,在我做的图像的变化检测方向就是输入差异图(两幅图像对应位置做差或者做比,或者做对数比),输出就是阈值。
在这个函数中,是使用最大类间方差法找到图片的一个合适的阈值(threshold)。
图像二值化:
bw3 = imbinarize(C, 0.3); 第一个参数为要处理的图像名称,第二个参数是用户选取的阈值。
imbinarize和im2bw 函数的作用是把大于阈值的元素换成1,小于阈值的函数换成0。
图像求连通域:
total = bwarea(BW)%计算二值图像中对象的总面积
连通域过滤:
BW2 = bwareaopen(BW,P,conn)%删除二值图像BW中面积小于P的对象,默认情况下conn使用8邻域。
寻找最大的连通域:
[L,num]=bwlabel(tu3);
stats=regionprops(L);
Ar=cat(1,stats.Area);
index=find(Ar==max(Ar));
tu(find(L~=index))=0;//将其他区域置为0
图像极坐标转换:
矩阵的操作:
创建矩阵:
建立向量的时候可以利用冒号表达式,冒号表达式可以产生一个行向量,一般格式是: e1:e2:e3,其中e1为初始值,e2为步长,e3为终止值。
还可以用linspace函数产生行向量,其调用格式为:linspace(a,b,n) ,其中a和b是生成向量的第一个和最后一个元素,n是元素总数。
ones()函数:产生全为1的矩阵,ones(n):产生n*n维的全1矩阵,ones(m,n):产生m*n维的全1矩阵;
zeros()函数:产生全为0的矩阵;
rand()函数:产生在(0,1)区间均匀分布的随机阵;
eye()函数:产生单位阵;
randn()函数:产生均值为0,方差为1的标准正态分布随机矩阵。
获取矩阵的元素:
可以通过下标(行列索引)引用矩阵的元素,如 Matrix(m,n)。
也可以采用矩阵元素的序号来引用矩阵元素。
矩阵元素的序号就是相应元素在内存中的排列顺序。
在MATLAB中,矩阵元素按列存储。
序号(Index)与下标(Subscript )是一一对应的,以m*n矩阵A为例,矩阵元素A(i,j)的序号为(j-1)*m+i。
其相互转换关系也可利用sub2ind和ind2sub函数求得。
矩阵的拆分:
利用冒号表达式获得子矩阵:
A(:,j)表示取A矩阵的第j列全部元素;A(i,:)表示A矩阵第i行的全部元素;A(i,j)表示取A矩阵第i行、第j列的元素。
A(i:i+m,:)表示取A矩阵第i~i+m行的全部元素;A(:,k:k+m)表示取A矩阵第k~k+m列的全部元素,A(i:i+m,k:k+m)表示取A矩阵第i~i+m行内,
并在第k~k+m列中的所有元素。此外,还可利用一般向量和end运算符来表示矩阵下标,从而获得子矩阵。end表示某一维的末尾元素下标。
利用空矩阵删除矩阵的元素:
在MATLAB中,定义[]为空矩阵。给变量X赋空矩阵的语句为X=[]。注意,X=[]与clear X不同,clear是将X从工作空间中删除,
而空矩阵则存在于工作空间中,只是维数为0。
特殊矩阵:
魔方矩阵魔方矩阵有一个有趣的性质,其每行、每列及两条对角线上的元素和都相等。对于n阶魔方阵,其元素由1,2,3,…,n2共n2个整数组成。MATLAB提供了求魔方矩阵的函数magic(n),其功能是生成一个n阶魔方阵。
范得蒙矩阵范得蒙(Vandermonde)矩阵最后一列全为1,倒数第二列为一个指定的向量,其他各列是其后列与倒数第二列的点乘积。可以用一个指定向量生成一个范得蒙矩阵。在MATLAB中,函数vander(V)生成以向量V为基础向量的范得蒙矩阵。
希尔伯特矩阵在MATLAB中,生成希尔伯特矩阵的函数是hilb(n)。使用一般方法求逆会因为原始数据的微小扰动而产生不可靠的计算结果。MATLAB中,有一个专门求希尔伯特矩阵的逆的函数invhilb(n),其功能是求n阶的希尔伯特矩阵的逆矩阵。
托普利兹矩阵托普利兹(Toeplitz)矩阵除第一行第一列外,其他每个元素都与左上角的元素相同。生成托普利兹矩阵的函数是toeplitz(x,y),它生成一个以x为第一列,y为第一行的托普利兹矩阵。这里x, y均为向量,两者不必等长。toeplitz(x)用向量x生成一个对称的托普利兹矩阵。
伴随矩阵 MATLAB生成伴随矩阵的函数是compan(p),其中p是一个多项式的系数向量,高次幂系数排在前,低次幂排在后。
帕斯卡矩阵我们知道,二次项(x+y)n展开后的系数随n的增大组成一个三角形表,称为杨辉三角形。由杨辉三角形表组成的矩阵称为帕斯卡(Pascal)矩阵。函数pascal(n)生成一个n阶帕斯卡矩阵。
矩阵的运算:
find函数:
[i,j,s]=find(S)
[i,j]=find(S) %返回 S 中所有非零元素的下标和数值
matlab中矩阵的表示及简单操作
卷积运算:
滤波:
BW = edge(I,'sobel') 自动选择阈值用Sobel算子进行边缘检测
BW = edge(I,'sobel',thresh) 根据所指定的敏感度阈值thresh,用Sobel算子进行边缘检测,它忽略了所有小于阈值的边缘。当thresh为空时,自动选择阈值。
BW = edge(I,'sobel',thresh,direction) 根据所指定的敏感度阈值thresh,在所指定的方向direction上,用Sobel 算子进行边缘检测。Direction可取的字符串值为horizontal(水平方向)、vertical(垂直方向)或both(两个方向)。
[BW,thresh] = edge(I,'sobel',...) 返回阈值
BW = edge(I,'prewitt') 自动选择阈值用prewitt算子进行边缘检测
BW = edge(I,'prewitt',thresh) 根据所指定的敏感度阈值thresh,用prewitt算子进行边缘检测,它忽略了所有小于阈值的边缘。当thresh为空时,自动选择阈值
BW = edge(I,'prewitt',thresh,direction) 根据所指定的敏感度阈值thresh,在所指定的方向direction上,用prewitt算子进行边缘检测。Direction可取的字符串值为horizontal(水平方向)、vertical(垂直方向)或both(两个方向)默认方向为both
[BW,thresh] = edge(I,'prewitt',...) 返回阈值
BW = edge(I,'roberts') 自动选择阈值用roberts算子进行边缘检测
BW = edge(I,'roberts',thresh) 根据所指定的敏感度阈值thresh,用Roberts算子进行边缘检测,它忽略了所有小于阈值的边缘。当thresh为空时,自动选择阈值。
[BW,thresh] = edge(I,'roberts',...) 返回阈值
BW = edge(I,'log') 自动选择阈值用LOG算子进行边缘检测
直方图均衡化:
I=imread('1.jpg');
J=histeq(I); %直方图均衡化
椭圆拟合:cftools 生成matlab代码
houghcircle:
function [hough_space,hough_circle,para] = hough_circle(BW,step_r,step_angle,r_min,r_max,p,var,res)
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% input
% BW:二值图像;
% step_r:检测的圆半径步长
% step_angle:角度步长,单位为弧度
% r_min:最小圆半径
% r_max:最大圆半径
% p:阈值,0,1之间的数 通过调此值可以得到图中圆的圆心和半径
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% output
% hough_space:参数空间,h(a,b,r)表示圆心在(a,b)半径为r的圆上的点数
% hough_circl:二值图像,检测到的圆
% para:检测到的圆的圆心、半径
circleParaXYR=[];
para=[];
[m,n] = size(BW);
size_r = round((r_max-r_min)/step_r)+1;%四舍五入
size_angle = round(2*pi/step_angle);
hough_space = zeros(m,n,size_r);
[rows,cols] = find(BW);%查找非零元素的行列坐标
ecount = size(rows);%非零坐标的个数
% Hough变换
% 将图像空间(x,y)对应到参数空间(a,b,r)
% a = x-r*cos(angle)
% b = y-r*sin(angle)
for i=1:ecount
for r=1:size_r %半径步长数
for k=1:size_angle %按一定弧度把圆几等分
a = round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle));
b = round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle));
if(a>0&a<=m&b>0&b<=n)
hough_space(a,b,r) = hough_space(a,b,r)+1;%h(a,b,r)的坐标,圆心和半径
end
end
end
end
% 搜索超过阈值的聚集点。对于多个圆的检测,阈值要设的小一点!通过调此值,可以求出所有圆的圆心和半径
max_para = max(max(max(hough_space)));%返回值就是这个矩阵的最大值
index = find(hough_space>=max_para*p);%一个矩阵中,想找到其中大于max_para*p数的位置
length = size(index);%符合阈值的个数
hough_circle = false(m,n);
%hough_circle = zeros(m,n);
%通过位置求半径和圆心。
% var=5;
for i=1:ecount
for k=1:length
par3 = floor(index(k)/(m*n))+1;
par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;
par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;
if((rows(i)-par1)^2+(cols(i)-par2)^2<(r_min+(par3-1)*step_r)^2+var&...
(rows(i)-par1)^2+(cols(i)-par2)^2>(r_min+(par3-1)*step_r)^2-var)
hough_circle(rows(i),cols(i)) = true; %检测的圆
end
end
end
% 从超过峰值阈值中得到
for k=1:length
par3 = floor(index(k)/(m*n))+1;%取整
par2 = floor((index(k)-(par3-1)*(m*n))/m)+1;
par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m;
circleParaXYR = [circleParaXYR;par1,par2,par3];
hough_circle(par1,par2)= true; %这时得到好多圆心和半径,不同的圆的圆心处聚集好多点,这是因为所给的圆不是标准的圆
%fprintf(1,'test1:Center %d %d \n',par1,par2);
end
%集中在各个圆的圆心处的点取平均,得到针对每个圆的精确圆心和半径!
while size(circleParaXYR,1) >= 1
num=1;
XYR=[];
temp1=circleParaXYR(1,1);
temp2=circleParaXYR(1,2);
temp3=circleParaXYR(1,3);
c1=temp1;
c2=temp2;
c3=temp3;
% temp3= r_min+(temp3-1)*step_r;
if size(circleParaXYR,1)>1
for k=2:size(circleParaXYR,1)
if (circleParaXYR(k,1)-temp1)^2+(circleParaXYR(k,2)-temp2)^2 > (r_min+(res-1)*step_r)^2 |...%圆心距离判断,大于res则判断两个点不是同一个圆的圆心
abs(circleParaXYR(k,3)-temp3)>res %半径长度判断,半径差大于res时,进一步排除同心圆
% if (circleParaXYR(k,1)-temp1)^2+(circleParaXYR(k,2)-temp2)^2 > temp3^2
XYR=[XYR;circleParaXYR(k,1),circleParaXYR(k,2),circleParaXYR(k,3)]; %保存剩下圆的圆心和半径位置
else
c1=c1+circleParaXYR(k,1);
c2=c2+circleParaXYR(k,2);
c3=c3+circleParaXYR(k,3);
num=num+1;
end
end
end
%fprintf(1,'sum %d %d radius %d\n',c1,c2,r_min+(c3-1)*step_r);
c1=round(c1/num);
c2=round(c2/num);
c3=round(c3/num);
c3=r_min+(c3-1)*step_r;
%fprintf(1,'num=%d\n',num)
%fprintf(1,'Center %d %d radius %d\n',c1,c2,c3);
para=[para;c1,c2,c3]; %保存各个圆的圆心和半径的值
circleParaXYR=XYR;
end
end
多项式拟合:
p = polyfit(xsegtemp,ysegtemp,3);%三次曲线拟合
ysegtempf = polyval(p,xsegtemp); %得到xsegtemp时拟合曲线的y值
圆形拟合:
数值运算:
uint8的范围是0-255 uint16的范围是0-65535
uint8(number) %这个函数的做法是把大于255的数全部强制置为255,而小于255的部分则保持原样不变
若希望将0-65535的灰度级映射到0-255上,则可采用以下的办法:uint8(double(number)/65535*255)
图像处理中用到的几个重要的函数记录:
g=imfilter(f,w,filtering_mode,boundary_options,size_optinos)
%对任意类型数组或多维图像进行滤波
%f是输入图像,w为滤波模板,g为滤波结果;
mean %求数组的均值
M=mean(A)
如果 A 是向量,则 mean(A) 返回元素均值。
如果 A 为矩阵,那么 mean(A) 返回包含每列均值的行向量。
如果 A 是多维数组,则 mean(A) 沿大小不等于 1 的第一个数组维度计算,并将这些元素视为向量。此维度会变为 1,而所有其他维度的大小保持不变。
M=mean(A,2) %返回列均值
[r,c]=size(A),当有两个输出参数时,size函数将矩阵的行数返回到第一个输出变量r,将矩阵的列数返回到第二个输出变量c。
size(X,1),返回矩阵X的行数;
size(X,2),返回矩阵X的列数;
ceil(X) %取顶
floor(X) %取底
mean(A,1):沿着第一维(列)求平均值;
mean(A,2):沿着第二维(行)求平均值;
画圆函数:
viscircles([0,0],3);
function [] = circle( x,y,r )
rectangle('Position',[x-r,y-r,2*r,2*r],'Curvature',[1,1],'linewidth',1),axis equal
end
function [] = plot1( x,y,r )
theta=0:0.1:2*pi;
Circle1=x+r*cos(theta);
Circle2=y+r*sin(theta);
c=[123,14,52];
plot(Circle1,Circle2,'c','linewidth',1);
axis equal
end
指定图像的大小:
set(gcf,'position',[80 100 800 600])
imhist( i );直接显示图像i的灰度直方图;
imhist(i,n)n为指定灰度级显示直方图;
[count, x] = imhist( i ) 获取直方图信息,count为每一级灰度像素个数,x为灰度级,x也可以在imhist(i,x)中指定,可以通过stem(x,count)画相应直方图;
一级引用
二级引用
三级引用
这里是百度一下,你就知道