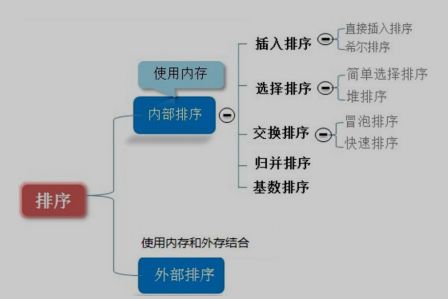
内部排序: 就是使用内存空间来排序
外部排序: 就是数据量很大,需要借助外部存储(文件)来排序.
直接上代码:
package com.lvcai;
public class Sort {
public static void main(String[] args) {
//排序 分为: 内部排序(使用内存来排序) , 外部排序(需要借助外部存储)
// 内部排序:
// int[] array = {100, 6, 9, 2, 1, 0, 54,23,5};
// int[] arr = new int[10000000];
// for (int i = 0; i < 10000000; i++) {
// arr[i] = (int) (Math.random() * 80000000); // 生成一个[0, 8000000) 数
// }
// int[] temp = new int[arr.length];
// long before = System.currentTimeMillis();
// //selectSort(arr); // 选择排序:8万个随机数,选择排序耗时 13755 毫秒
// //bubbleSort(arr); // 冒泡排序:8万个随机数,选择排序耗时 13804 毫秒
// //insertSort(arr); // 插入排序:8万个随机数,选择排序耗时 2381 毫秒
// //shellSort(arr); // 希尔排序:8万个随机数,选择排序耗时 8606 毫秒
// quickSort(arr,0,arr.length-1); // 快速排序:8万个随机数,选择排序耗时 16 毫秒
// //MergeSort(arr,0,arr.length-1,temp); // 归并排序:8万个随机数,选择排序耗时 23 毫秒
radixSort(arr); // 基数排序: 8万个随机数,选择排序耗时 16 毫秒
// long after = System.currentTimeMillis();
// System.out.println(after - before);
//int[] array = {100, 6, 9, 2, 1, 0, 54,23,5};
//int[] array = {8,1,2,4,5,6,7};
int[] array = {6,1,2,7,9,3,4,5,10,8};
int[] temp = new int[array.length];
print(array);
MergeSort(array,0,array.length-1,temp);
print(array);
}
//1: 选择排序: 将第一个数,和数组中其余数比较, 比较结束后, 数组第一个数就是最小的那个数, 将第二个数 和数组中其余数比较, 比较结束后也是将最小的数组放在最前面
// 测试结果: 8万个随机数,选择排序耗时8049毫秒 10万个随机数,选择排序耗时9636毫秒,
public static void selectSort(int[] array){
for (int i = 0; i < array.length - 1; i++) {
for (int j = i+1; j < array.length; j++) {
if(array[i] > array[j]){
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}
}
}
//2: 冒泡排序: 将待排序的序列 从前向后,依次比较相邻的二个元素, 如果逆序就交换, 这样是较大的值逐渐从前向后移动, 时间复杂度 O(n^2)
//测试结果: 8万个随机数,选择排序耗时9211毫秒 10万个随机数,选择排序耗时11603毫秒,
public static void bubbleSort(int[] array){
int temp= 0;
for (int i = 0; i < array.length -1; i++) {
for(int j = 0; j < array.length -1 -i ; j++){
if(array[j] > array[j+1]){
temp = array[j+1];
array[j+1] = array[j];
array[j] = temp;
}
}
}
}
//2.1: 冒泡排序优化: 如果在某一次循环比较过程中, 没有发生交换,说明此时,已经是有序的,,就提前结束
public static void bubbleSortBetter(int[] array){
int temp= 0;
for (int i = 0; i < array.length -1; i++) {
int exchageCount = 0;//交换次数,
for(int j = 0; j < array.length -1 -i ; j++){
if(array[j] > array[j+1]){
exchageCount++;
temp = array[j+1];
array[j+1] = array[j];
array[j] = temp;
}
}
if(exchageCount == 0){
break;
}
}
}
// 3: 插入排序: 将数组第一个数看做是有序的 ,后面的数都是无序的, 对于无序数据,在已排序的数据中从后向前扫描
// 速度测试结果:
//就像打牌一样, 将第一个元素看做有序的, 其余的牌看成无序的,从无序中最左侧拿出一张牌, 从后向前扫描有序序列,寻找插入位置,找到位置后,将牌插入,,
public static void insertSort(int[] array){
//思路: 1,假设第一个元素是有序的, 从第二个元素a开始比较
// 2, 如果这个元素a ,比前一个元素b小, 就将b后移一位,(会覆盖掉a,所以先将a保存下), 之后继续从后向前扫描,和a比较, 如果比a大,那么就后移,
// 3, 当循环结束的时候, 就说明已经找到插入位置了
/**
* 比如: {3,1,0,6}
* 一: 从1,和 3比较 , 1 < 3, 所以将 3 后移, 变为{3,3,0,6}, 跳出循环,此时将第一个3 替换为1 -->{1,3,0,6}
* 二: 然后 0 和3 比较, 3向后移动->{1,3,3,6}, 0 和1比较, 1向后移动->{1,1,3,6}, 跳出循环,此时将 1替换为0,->{0,1,3,6}
* 三: 然后 6和 3比较, 不变, 和1比较,不变, 和0 比较不变. 所以最终结果为 {0,1,3,6}
*
*/
for (int i = 1; i < array.length; i++) {
int insertVal = array[i];//要插入的元素, 先保存下
int insertIndex = i-1;// 要插入元素的前一元素的索引
//insertVal < array[insertIndex] 表示 要插入的元素 如果小于,之前索引对应元素, 就将array[insertIndex] 向后移一位
while(insertIndex >= 0 && insertVal < array[insertIndex]){
array[insertIndex+1] = array[insertIndex];//就将array[insertIndex] 向后移一位,会覆盖掉要插入的元素
insertIndex--;//递减,就是从后向前 扫描已排序的序列
}
//当跳出循环的时候, 说明 比insertVal大的元素, 都依次后移了一位, 而要插入的位置 刚好就是 insertIndex+1 的位置
array[insertIndex +1] = insertVal;
}
}
//4: 希尔排序: 又叫增量递减排序,是插入排序的优化, {3,1,6,0},由于最小数0 在最后,插入排序时,0 需要从最后移动到最前,这样效率反而低.
public static void shellSort(int[] array){
/**
* 思路:{8,1,2,4,5,6,7}, 长度 7
* 1: 步长增量 7/2 = 3, 从8开始,步长为3分组. 8,4,7 1,5 2,6 对这进行插入排序,结果为 {4,1,2,7,5,6,8}
* 2: 步长增量 3/2 = 1, 从4开始,步长为1分组, 就是对{4,1,2,7,5,6,8} 进行插入排序 结果为{1,2,4,5,6,7,8}
*
* {8, 9, 1, 7, 2, 3, 5, 4, 6, 0} 长度为10
* 1: 步长增量 10/2 = 5, 从8开始,步长为5分组, 8,3 9,5 1,4 7,6 2,0 对这五组分别进行插入排序,结果为:{3,5,1,6,0,8,9,4,7,2}
* 2: 步长增量 5/2 = 2, 从3开始,步长为2分组, 3,1,0,9,7 5,6,8,4,2 对这二组 分别进行插入排序, 结果为{0,2,1,4,3,5,7,6,9,8}
* 3: 步长增量 2/2 = 1, 从0开始,步长为1分组, 0,2,1,4,3,5,7,6,9,8 就是对他进行插入排序, 结果为{0,1,2,3,4,5,6,7,8,9}
*
* 可以看出 0 最小, 在第一次分组结束后, 0 已经到了中间,减少了移动次数
*/
int temp;
for(int grp =array.length/2 ; grp>0 ; grp /=2){//步长为长度/2
for(int i = grp ; i < array.length ; i++){
for(int j = i - grp; j >= 0 ; j -= grp){
if(array[j] > array[j+grp]){ //组间元素对比,如果逆序, 就交换
temp = array[j+grp];
array[j+grp] = array[j];
array[j] = temp;
}
}
}
}
}
//5: 快速排序: 是冒泡排序的改进,是一种分区交换排序方法, 思想如下: 一趟快速排序,采用从两头向中间扫描的方法,公式交换与基准记录
// 快速排序之所以快,是因为冒泡排序时相邻二个元素,依次比较,,,而快速排序,是根据基准值,将序列变成 左侧比他小,右侧比他大,这样的比较是跳跃式的,总的比较次数是比冒泡要少
/**
* @param array 待排序列
* @param leftIndex 待排序列起始位置
* @param reightIndex 待排序列结束位置
*/
public static void quickSort(int[] array, int leftIndex, int reightIndex){
/**
* 思路: {6,1,2,7,9,3,4,5,10,8}
* 1: 将第一个数 6 作为基准值,坑位(下角标0), 向从后向前扫描,找到比6小的数 5, 5填到该坑位 {5,1,2,7,9,3,4,5,10,8},同时下角标 7,成为新的坑位
* 2: 从前向后扫描,找到一个比6 大的数:7, 将7 填到上一个坑位 -> {5,1,2,7,9,3,4,7,10,8},下角标3成为新坑位
* 3: 从7开始从后向前扫描, 找到一个比6 小的数:4, 将4填到上一个坑位,-->{5,1,2,4,9,3,4,7,10,8},下角标6成为新坑位
* 4: 从4开始从前向后扫描, 找到一个比6 大的数:9, 将9填到上一个坑位,-->{5,1,2,4,9,3,9,7,10,8},下角标4成为新坑位
* 5: 从9开始从后向前扫描,找到一个比6 小的数:3, 将3填到上一个坑位, -->{5,1,2,4,3,3,9,7,10,8},下角标5成为新坑位
* 6: 此时循环结束, 然后将 基准值:6,填到上一个坑位 -->{5,1,2,4,3,6,9,7,10,8}
* 7:此时 以6 区分 {5,1,2,4,3},{9,7,10,8} 分别进行 1-6步骤
*/
if(leftIndex >= reightIndex){
return;
}
int left = leftIndex;// 记录开始索引, 因为排序过程中 leftIndex 会移动, 所以要用第三方变量left来代替参与排序
int reight = reightIndex;//记录尾索引,
int key = array[left]; //这个是基准值,通常将第一个作为基准值, 同时left成为新坑位(下标为0)
while(left < reight){
//先从后向前扫描, 找到一个比基准值小的值, 将这个值赋填到上个left坑位, 同时reight成为新坑位
while(key <= array[reight] && left < reight){
reight--;
}
array[left] = array[reight];
//从前向后扫描, 找到一个比基准值 大的值, 将这个值赋值给,上一个reight位置(填到坑中),同时这个left成为新坑位
while( key >= array[left] && left < reight){
left++;
}
array[reight] = array[left];
}
//当这个大的循环结束的时候, left== reight , 并且这个位置就是新的坑位,需要将基准值key 填到这里
array[left] = key;
//此时该序列变成一个: left 左侧都是比array[left]小, 右侧都是比array[reight]大 的序列
// 左递归, 开始下标 leftIndex, 结束下标 left-1
quickSort(array,leftIndex,left-1);
// 右递归, 开始下标 left+1, 结束下标 reightIndex
quickSort(array,reight+1,reightIndex);
}
//6: 归并排序, 归并排序需要额外的空间,temp 大小和array一样,
/**
*
* @param array 待排序 序列
* @param begin 开始索引
* @param end 尾部索引
* @param temp 额外空间, 大小和待排序一样
*/
public static void MergeSort(int[] array,int begin,int end,int[] temp){
if(begin < end){
int mid = (begin + end)/2;
//递归 将序列不停的二分
MergeSort(array,begin,mid,temp);
MergeSort(array,mid+1,end,temp);
//合并,
merge(array,begin,mid,end,temp);
}
}
public static void merge(int[] array,int begin,int mid,int end,int[] temp){
/**
* 思路: {6,1,2,7,9,3,4,5,10,8}
* 1: 先分成 左右两部分 {6,1,2,7,9} {3,4,5,10,8},继续分
* 2: {6,1,2} {7,9} {3,4,5} {10,8},继续分
* 3: {6,1} {2} {7,9} {3,4} {5} {10,8}
*
* 左序列 排序合并过程: {6,1} {2} {7,9}
* 4.1:{6,1}排序过程: 将小的数加入到temp中 {1}, 然后发现左序列还有剩余数6, 将6 加入到temp中{1,6}, 然后将temp的数,复制到array中 {1,6,2,7,9,3,4,5,10,8}
* 4.2: 由于接下来为{2}排序, 将{1,6} 和{2} 排序: 1比2小, 1添加到temp中{1}, 2比6小,2添加到temp中{1,2}, 最后左序列还有剩余6, 6添加到temp中{1,2,6}, 将temp复制到array中{1,2,6,7,9,3,4,5,10,8}
* 4.3: 接下来为{1,2,6} {7,9} 排序合并.....{1,2,6,7,9}
*
* 4.4 右序列 排序合并过程 {3,4} {5} {10,8} ---> {3,4} {5} {8,10}. 最终变成{3,4,5,8,10}
*
* 5 将{1,2,6,7,9} {3,4,5,8,10} 排序合并,然后复制到array中,,最终结果{1,2,3,4,5,6,7,8,9,10}
*/
int i = begin;//初始化,左边序列的初始索引
int j = mid + 1; //初始化, 右边序列的初始索引
int t = 0;//temp序列的初始索引
//先把左序列 右序列的数据, 进行排序填充到temp中,直到左右两边有一边处理完毕
while(i <= mid && j <= end){
if(array[i] <= array[j]){
temp[t] = array[i];
t++;
i++;
}else{
temp[t] = array[j];
t++;
j++;
}
}
//如果左序列有剩余,就加入到temp
while(i <= mid){
temp[t] = array[i];
t++;
i++;
}
//如果右序列有剩余,就加入到temp
while(j <= end){
temp[t] = array[j];
t++;
j++;
}
//将temp已排好序的,复制到array中
t = 0;
//int tempLeft = begin;
while(begin <= end){
array[begin] = temp[t];
t++;
begin++;
}
}
public static void print(int[] array){
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
}
}
7;基数排序: 也叫桶排序,思路分析
//7: 基数排序, 也叫桶排序, 由于单个数字只有0-9, 需要有10个桶,编号从0-9,
public static void radixSort(int[] array){
/**
* 思路: 基数排序, 也叫桶排序, 思路请看图:
*/
//1, 获取数组中的最大数
int max = array[0];
for (int i = 1; i < array.length; i++) {
if(array[i] > max){
max = array[i];
}
}
//桶排序的次数为
int maxLenght = (max+"").length();
//2: 创建一个二维数组,来表示10个桶,为避免下标越界,每个桶的大小都为array.length
int[][] bucket = new int[10][array.length];
//2.1: 需要记录每个桶中的数据个数,便于取数据,这里用一个 一维数组来表示, 比如bucketNumberCount[1] = 2, 表示编号为1 的桶有2个数据
int[] bucketNumberCount = new int[10];
for (int i = 0 , n = 1; i < maxLenght; i++ , n *= 10) {
for (int j = 0; j < array.length; j++) {
//获取对应的位数, 个位,十位,百位,千位. 当n为1时候,是个位数, n为10,是十位数, n为100是百位数
int numberDigit = array[j] / n % 10;
//根据 位数,将数放入对应的桶中,numberDigit就是对应的桶编号,bucketNumberCount这个数组初始为[0,0,0,0,0,0,0,0,0,0], bucketNumberCount[numberDigit] = 0,表示这个桶中元素个数为0,bucketNumberCount[numberDigit] = 1,说明该桶中放了一个元素
bucket[numberDigit][bucketNumberCount[numberDigit]] = array[j]; //这个数放到桶中下标为0 的位置,之后放到为1的位置
bucketNumberCount[numberDigit]++;
}
//循环结束时候,说明都放到对应的桶中了, 接下来根据桶编号0-9, 将数据取出来,放到array中
int index = 0;
for (int k = 0; k < 10; k++) {
if(bucketNumberCount[k] != 0){
//说明 编号为k的桶中有数据,数量为bucketNumberCount[k], 循环取出,存到array中
for (int h = 0; h < bucketNumberCount[k]; h++) {
array[index] = bucket[k][h];
index++;
}
}
//编号为k的桶中元素取出来后,将桶中元素清0;避免影响下次存取
bucketNumberCount[k] = 0;
}
}
}