lsd-slam源码解读第一篇:Sophus/sophus

lsd-slam源码解读第一篇:Sophus/sophus

---

所谓slam即Real-time Simultaneous Localization and Mapping,实时定位与地图重建，lsd是一个大规模的单目视觉半稠密slam项目，优点和前景我就不多说了，做机器人和AR的朋友们估计早就已经铭记于心，在进入正题之前，我在这里给出官网和代码链接，有兴趣的朋友可以上去看看
官网:http://vision.in.tum.de/research/vslam/lsdslam
代码:https://github.com/tum-vision/lsd_slam

我想在明白任何一个slam算法之前，我们应该首先知道的是几个变换，即平移，旋转，相似以及投影变换
在lsd-slam中，有个三方开源库叫做Sophus/sophus，封装好了前三个变换

不失一般性，为了简单起见，我认为理解了一个文件，其他文件都是类似的，只是有一些由于自由度差异带来的差异而已，我在这里就介绍以一下so3.hpp文件

---

这几行内容只是一些简单的类型定义或者声明，其中使用了trait技法，不明白trait技法的好处的朋友可以去翻看stl源码解析书上的相关内容

namespace Sophus {
template class SO3Group;
typedef EIGEN_DEPRECATED SO3Group SO3;
typedef SO3Group SO3d; 
typedef SO3Group SO3f;  
}

template
struct traits, _Options> >
    : traits > {
  typedef _Scalar Scalar;
  typedef Map,_Options> QuaternionType;
};

template
struct traits, _Options> >
    : traits > {
  typedef _Scalar Scalar;
  typedef Map,_Options> QuaternionType;
};
}
}

SO3GroupBase

SO3是一个群，所谓群就是数学意义上的那个群，SO3正好是一个乘法群而已，满足封闭性，单位元，结合律等，我觉得没太大必要去了解数学上一个群甚至李群是如何抽象地定义的(因为那需要你1年左右的高等代数功底和一年左右的抽象代数功底，还有一年左右微分几何的功力)，但是理解这个群是如何用于做旋转的，我认为还是很有必要的

template
class SO3GroupBase {
public:
  typedef typename internal::traits::QuaternionType &
  QuaternionReference;
  typedef const typename internal::traits::QuaternionType &
  ConstQuaternionReference;

  static const int DoF = 3;
  static const int num_parameters = 4;
  static const int N = 3;

  typedef Matrix Transformation;
  typedef Matrix Point;
  typedef Matrix Tangent;
  typedef Matrix Adjoint;

这个部分的程序，无非是定义了一些数据了类型以及三个常数，前面的数据类型是两个四元数的引用类型(四元数用于旋转是一个非常美妙的idea，有兴趣的朋友可以去查阅相关资料)
接下来定义自由度，由于是三维空间的旋转所以只有3个自由度，四元数有4个参数，以及变换矩阵是3*3矩阵
最后定义的是要用到的数据类型，分别是3*3的旋转矩阵，3*1的空间点，3*1的角速度，还有3*3的邻接矩阵
我猜想大多数朋友去谷歌Adjoint matrix得到的结果不是图里面的邻接矩阵（对此我想说，此邻接非彼邻接），就是李群里面一大堆抽象的运算定义（这个正解了，太抽象，忘掉他吧，后面我会说明一下这玩意儿是如何使用的）

---

接下来让我们来看下面这个函数，也就是代码里面的下一行

  inline  const Adjoint Adj() const {
    return matrix();
    }

追踪进去之后得到的是

  inline
  const Transformation matrix() const {
    return unit_quaternion().toRotationMatrix();
  }

这个代码在文件的211行，表达的是一个单位四元数到一个旋转矩阵的变换，再追踪进去，在文件的291行

  ConstQuaternionReference unit_quaternion() const {
return static_cast(this)->unit_quaternion();

}
这个时候，你会发现，这里看起来是一个特别危险的代码，然而并不是，这个其实是基类调用子类方法的经典实现。
怎么做呢？方法很简单，基类和子类同时有一个相同名字的函数，基类作为模板类。但这个模板类型只能传入它的派生类，然后调用基类的同名函数，强制吧指针转化为模板类型的指针，这样就成功地调用了子类的同名函数

  QuaternionBase::toRotationMatrix(void) const {
  Matrix3 res;

  const Scalar tx  = Scalar(2)*this->x();
  const Scalar ty  = Scalar(2)*this->y();
  const Scalar tz  = Scalar(2)*this->z();
  const Scalar twx = tx*this->w();
  const Scalar twy = ty*this->w();
  const Scalar twz = tz*this->w();
  const Scalar txx = tx*this->x();
  const Scalar txy = ty*this->x();
  const Scalar txz = tz*this->x();
  const Scalar tyy = ty*this->y();
  const Scalar tyz = tz*this->y();
  const Scalar tzz = tz*this->z();

  res.coeffRef(0,0) = Scalar(1)-(tyy+tzz);
  res.coeffRef(0,1) = txy-twz;
  res.coeffRef(0,2) = txz+twy;
  res.coeffRef(1,0) = txy+twz;
  res.coeffRef(1,1) = Scalar(1)-(txx+tzz);
  res.coeffRef(1,2) = tyz-twx;
  res.coeffRef(2,0) = txz-twy;
  res.coeffRef(2,1) = tyz+twx;
  res.coeffRef(2,2) = Scalar(1)-(txx+tyy);

  return res;
}

也就是这个算法，这个算法本身是很简单的，只要你明白四元数是如何表示旋转的，那么写一个函数，将四元数转化为旋转矩阵，就是这个矩阵了（附四元数表示旋转的方法http://blog.csdn.net/candycat1992/article/details/41254799）

  /**
   * \returns copy of instance casted to NewScalarType
   */
  template
  inline SO3Group cast() const {
    return SO3Group(unit_quaternion()
                                   .template cast() );
  }

cast()函数显然是个很简单的函数，就是返回一个不同类型的对象

  inline Scalar* data() {
    return unit_quaternion_nonconst().coeffs().data();
  }

  inline const Scalar* data() const {
    return unit_quaternion().coeffs().data();
  }

这两个函数是返回四元数的数据

  inline
  void fastMultiply(const SO3Group& other) {
    unit_quaternion_nonconst() *= other.unit_quaternion();
  }

这里无非是调用了四元数的乘法运算

  /**
   * \returns group inverse of instance
   */
  inline
  const SO3Group inverse() const {
    return SO3Group(unit_quaternion().conjugate());
  }

这个就是返回了个共轭的四元数，然后用这个四元数构造了个SO3Group的对象

  inline
  const Tangent log() const {
    return SO3Group::log(*this);
  }

这个函数跟踪进去会到475行的log()函数，之后会发现这个log函数调用了logAndTheta()函数，也就是这个函数

  inline static
  const Tangent logAndTheta(const SO3Group & other,
                            Scalar * theta) {
    const Scalar squared_n
        = other.unit_quaternion().vec().squaredNorm();
    const Scalar n = std::sqrt(squared_n);
    const Scalar w = other.unit_quaternion().w();

    Scalar two_atan_nbyw_by_n;

    if (n < SophusConstants::epsilon()) {

      if (std::abs(w) < SophusConstants::epsilon()) {
        throw SophusException("Quaternion is not normalized!");
      }
      const Scalar squared_w = w*w;
      two_atan_nbyw_by_n = static_cast(2) / w
                           - static_cast(2)*(squared_n)/(w*squared_w);
    } else {
      if (std::abs(w)::epsilon()) {
        if (w > static_cast(0)) {
          two_atan_nbyw_by_n = M_PI/n;
        } else {
          two_atan_nbyw_by_n = -M_PI/n;
        }
      }else{
        two_atan_nbyw_by_n = static_cast(2) * atan(n/w) / n;
      }
    }

    *theta = two_atan_nbyw_by_n*n;

    return two_atan_nbyw_by_n * other.unit_quaternion().vec();
  }

我觉得应该明白这个函数是干啥用的，看返回值，很清楚的说明了这个函数是为了得到一个旋转的角速度的，而传入值实际上是另一个四元数和一个作为输出参数的值，代表了角速度的大小，具体计算方案实际上是李群里面的一组映射中的对数映射，从SO(3)向so(3)的映射

  inline
  void normalize() {
    Scalar length = unit_quaternion_nonconst().norm();
    if (length < SophusConstants::epsilon()) {
      throw SophusException("Quaternion is (near) zero!");
    }
    unit_quaternion_nonconst().coeffs() /= length;
  }

归一化函数

  inline
  const Point operator*(const Point & p) const {
    return unit_quaternion()._transformVector(p);
  }

这个函数实际上比较重要，它正是一个SO(3)的对象对一个点做旋转变换的函数，这个函数底层调用了四元数进行操作

  inline
  void operator*=(const SO3Group& other) {
    fastMultiply(other);
    normalize();
  }

这个函数就是两个旋转过程的复合

  inline static
  const Adjoint d_lieBracketab_by_d_a(const Tangent & b) {
    return -hat(b);
  }

这个又是返回邻接矩阵，传入值是一个角速度，你可能会问，这个邻接矩阵又是啥意思呢，其实很简单，这个邻接矩阵不同于刚才(把四元数转化为旋转矩阵),这个矩阵是把一个角速度转化为角速度矩阵的函数，由于角速度和向量相乘是叉积，但有时候需要把这样的运算表示成矩阵乘法的方式，由此，需要把角速度(向量，实际上是一阶反对称张量)转化为矩阵的形式(实际上是还原成本来的张量表达形式)我想大多数朋友可能暂时不能理解其数学含义，但是这个的操作方式是很简单的

  inline static
  const Transformation hat(const Tangent & omega) {
    Transformation Omega;
    Omega <<  static_cast(0), -omega(2),  omega(1)
        ,  omega(2),     static_cast(0), -omega(0)
        , -omega(1),  omega(0),     static_cast(0);
    return Omega;
  }

以上，其实就是那个简单的操作，然后再取相反数而已

  inline static
  const SO3Group exp(const Tangent & omega) {
    Scalar theta;
    return expAndTheta(omega, &theta);
  }

  inline static
  const SO3Group expAndTheta(const Tangent & omega,
                                     Scalar * theta) {
    const Scalar theta_sq = omega.squaredNorm();
    *theta = std::sqrt(theta_sq);
    const Scalar half_theta = static_cast(0.5)*(*theta);

Scalar imag_factor;
Scalar real_factor;;
if((*theta)::epsilon()) {
  const Scalar theta_po4 = theta_sq*theta_sq;
  imag_factor = static_cast(0.5)
                - static_cast(1.0/48.0)*theta_sq
                + static_cast(1.0/3840.0)*theta_po4;
  real_factor = static_cast(1)
                - static_cast(0.5)*theta_sq +
                static_cast(1.0/384.0)*theta_po4;
} else {
  const Scalar sin_half_theta = std::sin(half_theta);
  imag_factor = sin_half_theta/(*theta);
  real_factor = std::cos(half_theta);
}



 return SO3Group(Quaternion(real_factor,
                                               imag_factor*omega.x(),
                                               imag_factor*omega.y(),
                                               imag_factor*omega.z()));
  }

这两个函数或许又会让你痛苦很长一段时间，因为它又是李群的映射运算，而且这个代码还有一点小bug
这两个函数的核心其实就是下面那个函数，它其实是遵从以下公式得到的

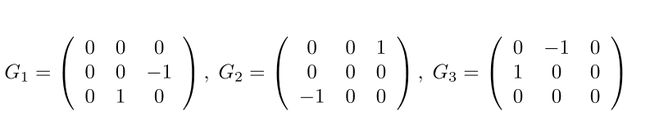
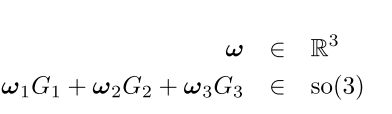
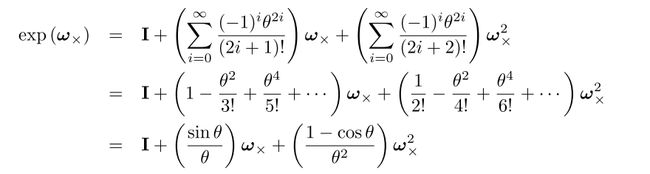
人生苦短，证明都见鬼去吧，有兴趣的朋友可以自行去查看相关资料，注意代码有点小bug

if((*theta)::epsilon()) {
  const Scalar theta_po4 = theta_sq*theta_sq;
  imag_factor = static_cast(0.5)
                - static_cast(1.0/48.0)*theta_sq
                + static_cast(1.0/3840.0)*theta_po4;
  real_factor = static_cast(1)
                - static_cast(0.5)*theta_sq +
                static_cast(1.0/384.0)*theta_po4;
}

其实if这里面这一大块是Taylor公式，上面是sin(x)/x的，下面是cos(x)的，但值得注意的是，这里的x都是取的半角，也就是x/2，所以指数部分还要多乘以一个1/2^n,但是static_cast(0.5)*theta_sq这个地方作者忘了乘以这个系数，其他地方都是乘了的

后面的函数，稍微复杂的，前面在写调用的时候，或多或少已经写过了，剩下的代码相对都比较简单，主要包含一些类型定义和一些简单的构造，请读者自行解读