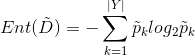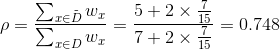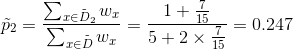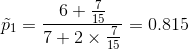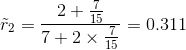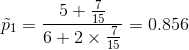机器学习笔记（7）——C4.5决策树中的缺失值处理

缺失值处理是C4.5决策树算法中的又一个重要部分，前面已经讨论过连续值和剪枝的处理方法：

机器学习笔记（5）——C4.5决策树中的连续值处理和Python实现

机器学习笔记（6）——C4.5决策树中的剪枝处理和Python实现

现实任务中，通常会遇到大量不完整的样本，如果直接放弃不完整样本，对数据是极大的浪费，例如下面这个有缺失值的西瓜样本集，只有4个完整样本。

在构造决策树时，处理含有缺失值的样本的时候，需要解决两个问题：

（1）如何在属性值缺失的情况下选择最优划分属性？

（2）选定了划分属性，若样本在该属性上的值是缺失的，那么该如何对这个样本进行划分？

以上两个问题在周志华老师的《机器学习》书中有详细的讲解。但是还有一个问题：

（3）决策树构造完成后，如果测试样本的属性值不完整，该如何确定该样本的类别？

书中没有介绍，好在昆兰在1993年发表的文章中提供了解决方案。下面我们对以上3个问题逐一讨论。

1. 选择最优划分属性

之前的算法中，我们选择信息增益最大的属性作为最优划分属性，那么对于有缺失值的属性，其信息增益就是无缺失值样本所占的比例乘以无缺失值样本子集的信息增益。

其中是属性a上无缺失值样本所占的比例；是属性a上无缺失值的样本子集。回顾一下ID3算法中，信息增益的计算方法：

        

色泽：

另分别表示“色泽”属性上取值为“青绿”、“乌黑”、“浅白”的样本子集。

同样可以计算出其他几个属性的信息增益：

属性	色泽	根蒂	敲声	纹理	脐部	触感
信息增益	0.252	0.171	0.145	0.424	0.289	0.006

 

 

 

因此，选择“纹理”作为根节点进行划分。编号为{1,2,3,4,5,6,15}的7个样本进入“纹理=清晰”的分支，编号为{7,9,13,14,17}的5个样本进入“纹理=稍糊”的分支，编号为{11,12,16}的3个样本进入“纹理=模糊”的分支。

那么选定了划分属性，若样本在该属性上的值是缺失的，那么该如何对这个样本进行划分？（也就是问题2）

重点来了：对于编号为8和10的缺失值样本，将分别以7/15、5/15、3/15的权重划分到以上3个分支。也就是说，将缺失值样本按不同的概率划分到了所有分支中，而概率则等于无缺失值样本在每个分支中所占的比例。

这里引入了权重的概念，在学习开始时，样本的默认权重为1，对于无缺失值的样本，划分到子节点时其权重保持不变。

样本有了权重，我们需要对信息增益的计算公式做一些改进。

   （无缺失值样本所占的比例，样本的个数按权重来计算）

（无缺失值样本中第k类所占的比例，样本的个数按权重来计算）

（无缺失值样本中属性a上取值为的样本所占的比例，样本个数按权重来计算）

下面我们再以“纹理=清晰”这个分支为例，看看下一步将如何划分：

色泽：

    （无缺失值样本中，好瓜的比例）

    （无缺失值样本中，坏瓜的比例）

    （无缺失值样本中，“色泽=乌黑”的样本的比例）

    （无缺失值样本中，“色泽=青绿”的样本的比例）

    （“色泽=乌黑”）

    （“色泽=青绿”）

                     

根蒂：

无缺失值，

无缺失值样本中，正负样本所占比例：

    

属性值为“蜷缩”、“稍蜷”、“硬挺”的样本比例：

         

    

    

敲声：

无缺失值样本中，正负样本所占比例：

    

属性值为“浊响”、“沉闷”、“清脆”的样本比例：

         

    

    

脐部：

无缺失值样本中，正负样本所占比例：

    

属性值为“凹陷”、“稍凹”、“平坦”的样本比例：

         

    

    

 触感：

无缺失值样本中，正负样本所占比例：

    

属性值为“硬滑”、“软粘”的样本比例：

         

    

    

因此，根蒂作为最优划分属性，继续划分。

对每个分支递归构建出决策树如下：

2. 如何对有缺失值的样本分类

对于问题3，决策树构造完成后，如果测试样本的属性值不完整，该如何确定该样本的类别？昆兰的文章中给出如下解决方案：

如果分类进入某个属性值未知的分支节点时，探索所有可能的分类结果并把所有结果结合起来考虑。这样，会存在多个路径，分类结果将是类别的分布而不是某一类别，从而选择概率最高的类别作为预测类别。

那么如果是使用上面构造的决策树，仍然无法确定测试样本在每条路径上的概率，因此需要对以上树结构稍作改进。这里我们使用昆兰原著中的数据集，能够更好的体现算法的原理。

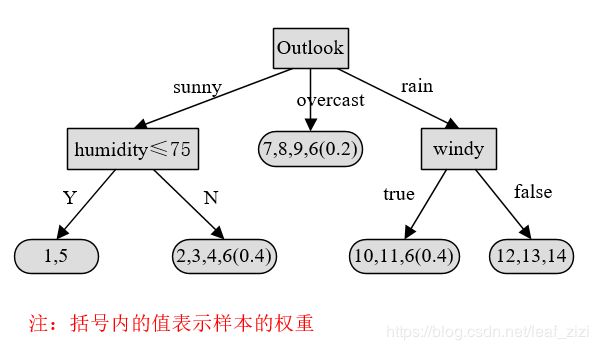
用前面的计算过程，会得到一个决策树，我们先看一下每个样本在树节点中的分布情况：

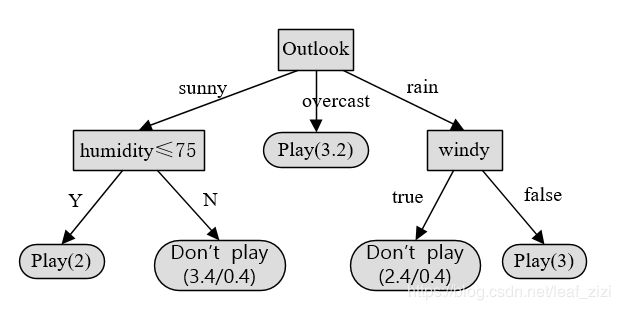
然后我们对树的结构做个改进，给每个叶子节点加个数值，例如（N/E)，N表示该叶节点中所包含的总样本数，E表示与该叶节点的类别不同的样本数，然后就可以得到这样的树结构。

现在我们使用这个决策树对测试样本分类，样本的属性值为：ountlook=sunny, temperature=70, humidity=?, windy=false.

测试样本进入左侧第一个分支，但是humidity属性值未知，因此两个分支的可能性都会考虑：

• 如果humidity<=75，类别是play。
• 如果humidity>75，类别是Don‘t play的概率为3/3.4（88%），play的概率是0.4/3.4（12%）。

那么，总的类别分布情况是：

因此，该样本的类别判定为Don't play。

总结

至此，对于决策树中缺失值的处理就有了完整的解决方案，主要解决了3个问题，1是如何选择最优划分属性，2是有缺失值的训练样本如何划分到分支中，3是测试样本如有缺失值该如何判断其类别。Python代码实现以后的文章中会补充。

---

代码资源下载地址（留言回复可能不及时，请您自行下载）：

https://download.csdn.net/download/leaf_zizi/10867159

---

参考：

周志华《机器学习》

J.Ross Quinlan C4.5: Programs For Machine Learning