一、声波波束求和
1. 声波传播和求和
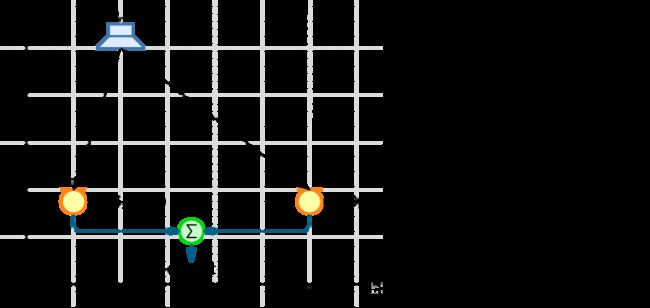
下图,一个简化的麦克风阵列波束形成设置。 从扬声器传播来的声波,将在不同的时刻到达麦克风,此属性是阵列空间滤波功能的本质。 模拟阵列的空间滤波性能时,有必要计算麦克风信号如何针对不同的信号源位置或角度求和。
根据扬声器和麦克风的位置,可以首先计算波束传播的距离,然后对于给定的声速,波束离开扬声器并到达每个麦克风所花费的时间。
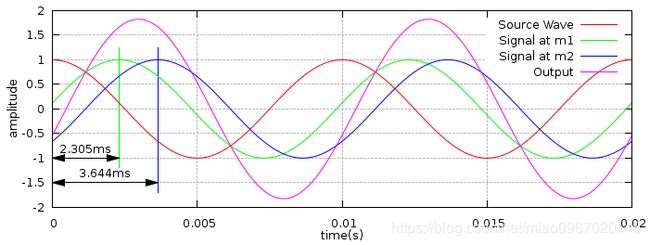
上图显示了一个100Hz的“源波”,代表信号离开扬声器。 该图还显示了“麦克风1处的信号”和“麦克风2处的信号”。 可以清楚地看到源信号传播到麦克风所引起的延迟。 最后显示了阵列的“输出”(两个麦克风信号的总和)。 由于传播时间的差异,输出的幅度为1.825,而不是幅度为源波的两倍(有两个麦克风)。
注意:未考虑信号从扬声器传播到麦克风时的衰减。
2.用相量计算组合麦克风信号幅度
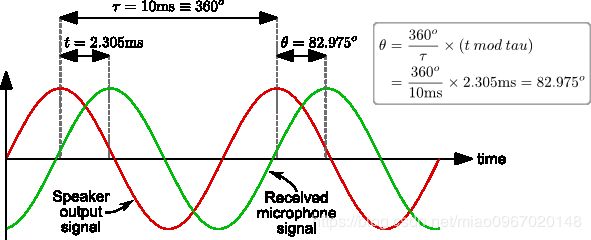
相量(Phasors )是一种简单的计算组合的麦克风信号(阵列的输出)幅度方法。 下图显示了如何计算两个信号之间的相位差。 波的一个周期对应于360°,给定的周期为10ms,2.305ms的延迟对应于82.975°的相移。
两种麦克风信号的相位计算如下所示:
相量图提供了一种表示正弦波的幅度和相位方法,还提供相加波形的图形方法。 三个相量图表示两个麦克风信号和阵列的输出。 相量长度对应于波的幅度,角度对应于相位,被绘制为复轴上的向量。 通过将向量相加,可以很容易地实现相量求和,所得向量代表相加波。
对向量求和的最简单方法是将其从极坐标(振幅和相位)转换为笛卡尔坐标(实数和虚数)。 然后,可以根据两个麦克风矢量的总和轻松计算出输出矢量。
最后,计算波幅总和,使用毕达哥拉斯定理计算总和向量的长度,如下所示
3.简化形式
综合上述阶段,可以得出以下公式:
根据波的频率,行间距离和声速来计算波的复数表示。 要输出一组波,只需计算并叠加每个波的实部和虚部,然后使用毕达哥拉斯定理计算最终振幅。
以下c代码执行上述两个麦克风设置的波加和计算:
File: waves.c
#include
#include
int main(void)
{
double phase, distance, delay;
double freq = 100.0; // Hz
double speedSound = 343.0; // m/s
// Microphone 1
distance = sqrt(0.25*0.25 + 0.75*0.75);
delay = distance / speedSound;
double re1 = cos(2.0 * M_PI * freq * delay);
double im1 = sin(2.0 * M_PI * freq * delay);
phase = 180 * atan2(im1, re1) / M_PI;
printf("Mic1 - Distance:%.4f, Delay:%.4f, Phase:%.3f, [%.3f %.3f]\n", distance, delay*1000, phase, re1, im1);
// Microphone 2
distance = sqrt(1.00*1.00 + 0.75*0.75);
delay = distance / speedSound;
double re2 = cos(2.0 * M_PI * freq * delay);
double im2 = sin(2.0 * M_PI * freq * delay);
phase = 180 * atan2(im2, re2) / M_PI;
printf("Mic2 - Distance:%.4f, Delay:%.4f, Phase:%.3f, [%.3f %.3f]\n", distance, delay*1000, phase, re2, im2);
// Output
double re = re1 + re2;
double im = im1 + im2;
double amp = sqrt(re*re + im*im);
phase = 180 * atan2(im, re) / M_PI;
printf("Output - Amplitude:%.3f, Phase:%.3f, [%.3f %.3f]\n", amp, phase, re, im);
return 0;
} 可以使用以下命令来编译和执行代码:
gcc -Wall -lm -o waves waves.c
./waves输出显示麦克风的极性和笛卡尔形式以及输出信号。
Mic1 - Distance:0.7906, Delay:2.3049, Phase:82.975, [0.122 0.992]
Mic2 - Distance:1.2500, Delay:3.6443, Phase:131.195, [-0.659 0.752]
Output - Amplitude:1.826, Phase:107.085, [-0.536 1.745]4. 欧拉公式表示
可以使用欧拉公式表示波的复数。 下面的等式显示了欧拉公式,以及如何调整它来表示频率为f的波动。
对于延迟为d的波,方程式:
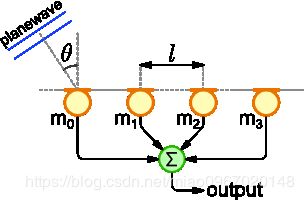
5. 线性阵列示例
以线性阵列为例, 每个阵列麦克风之间的距离为1米, 对于从角度θ以声速c到达的频率为f的平面波,使用以下公式计算阵列的输出。
下面代码用相量和指数方法计算线性阵列的输出幅度。
相量方法:
File: array1.c
#include
#include
int main(void)
{
int numElements = 4; // Number of array elements
double spacing = 0.75; // Element separation in metre
double angle = 30.0; // Degrees from broadside
double freq = 100.0; // Signal frequency in Hz
double speedSound = 343.0; // m/s
int i;
double realSum = 0;
double imagSum = 0;
// Iterate through array elements
for (i=0 ; i 指数方法
File: array2.c
#include
#include
#include
#include
int main(void)
{
int numElements = 4; // Number of array elements
double spacing = 0.75; // Element separation in metre
double angle = 30.0; // Degrees from broadside
double freq = 100.0; // Signal frequency in Hz
double speedSound = 343.0; // m/s
int i;
gsl_complex total;
GSL_SET_COMPLEX(&total, 0 ,0);
gsl_complex comp;
// Iterate through array elements
for (i=0 ; i 可以使用以下命令来编译和执行代码
> gcc -Wall -lm -o array1 array1.c
> ./array1
> gcc -Wall -lm -lgsl -o array2 array2.c
> ./array2这两个程序的输出是相同的,因为它们都计算相同的内容,尽管方式略有不同。 输出以米为单位显示每个阵列元素的物理位置,以及相对于第一个麦克风的波前延迟。 求和信号的幅度也以其复杂的形式显示。
0) Position: 0.000000, Delay: 0.000000e+00
1) Position: 0.750000, Delay: 1.093294e-03
2) Position: 1.500000, Delay: 2.186589e-03
3) Position: 2.250000, Delay: 3.279883e-03
Output Amplitude: 2.912 [1.498204, 2.497171]