算法图解第四章快速排序（递归的巧妙应用）（学习笔记）

一、分而治之

假设你是农场主，有一小块土地。你要将这块地均匀地分成方块，且分出的方块要尽可能大。

显然，下面的分法都不符合要求。

如何将一块地均匀地分成方块，并确保分出的方块是最大的呢？

使用D&C策略！D&C算法是递归的。

使用D&C解决问题的过程包括两个步骤。

(1)找出基线条件，这种条件必须尽可能简单。

(2) 不断将问题分解（或者说缩小规模），直到符合基线条件。

这里我就用我画的图解释下：

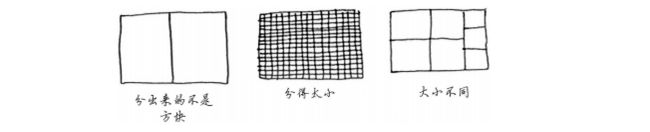
画的图可能不是很标准，你就当这里面都是正方形，我是怎么画的呢？

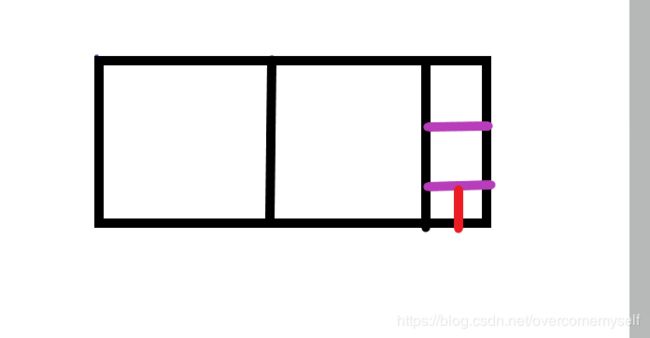
第一步：首先是一个矩形，既然让我们尽可能的画方块最大的，在矩形里要想画最大的正方形，就是让正方形的边长最长，正方形的边长最长不能超过矩形的的宽，所以，第一步就是画的那两条黑线。

第二步：画两条黑线还剩下一个矩形，跟第一步一样，继续使正方形的边长最长，就是画的那两条紫色线。

第三步：最后一个的矩形的长等于宽的两倍，所以正好是两个正方形。

而使用D&C解决问题的过程包括两个步骤：

(1) 找出基线条件，而这里的基线条件就是当长等于宽的两倍时

(2) 不断将问题分解（或者说缩小规模），直到符合基线条件。再这里每次分开最大正方形后会留下一个矩形，而这个矩形再重复原来的步骤即可。

二、快速排序

如何对一个数组进行快速排序呢？

快速排序也是用了D&C，所以必须先理解上面那个例子。

下面我们就来学习快速排序。

对一个数组进行快速排序，先找出基线条件，也就是最简单的数组，也就是不用排序的数组。所以：

基线条件：数组为空或者只包含一个元素（因为这样只需要原样返回数组即可，不用排序）

如果有多个元素的数组怎么办？

你就要使用D&C，将数组分解，直至满足基线条件，到这里D&C解决问题的过程的两个步骤基本确定了。

下面就介绍快速排序的工作原理：

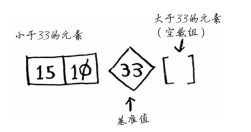
首先，从数组中选择一个元素，这个元素被称为基准值

稍后再介绍如何选择合适的基准值。我们暂时将数组的第一个元素用作基准值

接下来，找出比基准值小的元素以及比基准值大的元素,分别位于基准值两边，如图：

现在你有：

(1)一个由所有小于基准值的数字组成的子数组(可以为空)；

(2)基准值；

(3)一个由所有大于基准值的数组组成的子数组(可以为空)。

但是这里只是进行了分区，得到的两个子数组是无序的。

而如果这两个数组是有序的，对整个数组进行排序将非常容易。

只需要像这样：左边的数组 + 基准值 + 右边的数组，合并就可以了。

所以只要对这两个子数组进行快速排序，再合并结果，就能得到一个有序数组！

（而这两个子数组不就又可以当成原来的那个数组去重复以上的步骤。）

三、快速排序的代码：

def sort(a):
    if len(a)<2:
        return a  #基线条件：为空或只包含一个元素的数组是“有序”的
    else:
        x=a[0]
        less=[i for i in a[1:] if i <=x]  #由所有小于基准值的元素组成的子数组
        more=[i for i in a[1:] if i >x]   #由所有大于基准值的元素组成的子数组
        return sort(less)+[x]+sort(more)  #左边的数组（有序） + 基准值 + 右边的数组（有序）
print (sort([5,4,2,9,3,8,6,2,1,5]))

结果：

[1, 2, 2, 3, 4, 5, 5, 6, 8, 9]

其实对于基准值的选择，无论选择谁作为基准值都可以分别把小于基准值合成一个数组(可以为空数组)，大于基准值的一个数组(可以为空数组)，最终都可以用快速排序法进行排序。