视觉SLAM十四讲-第十讲笔记

本讲开始进入后端模块。后端优化目前分为基于滤波器的方法和基于非线性优化的方法，本讲讲述以EKF为代表的滤波器法，以及稀疏性。

一、 后端优化概述

1. 后端模块的作用

前端估计得到：

• $k$时刻相机的位姿，$x_k$
• 地图中路标$j$的世界坐标，$y_j$

前端估计只基于$k$的前一时刻或前几时刻。后端优化所做的，则是根据到目前为止观测到的所有信息，优化之前的估计结果。
后端优化中，把位姿$x$和路标$y$都看做服从某种概率分布的随机变量。已知相机运动数据$u$，观测数据$z$，问题转化为确定其概率分布，进行最大似然估计。

后端优化主要有两种方法：

1. 假设马尔科夫性，$k$时刻状态只与$k-1$时刻有关。即本讲的EKF法。
2. 假设$k$时刻状态与之前所有状态有关，为基于非线性优化的方法。将在下一讲详细阐释。

2. 问题描述

变量：
$x_k$：$k$时刻下所有未知量，包含相机和此时刻m个可见路标。
已知：
$u_{1:k}$：前$k$帧的运动数据。
$z_{1:k}$：前$k$帧的观测数据。
估计：
$P(x_k|x_0,u_{1:k},z_{1:k})$：根据所有已知，估计现在的位姿和路标的状态分布。

根据贝叶斯法则：
$$P(x_k|x_0,u_{1:k},z_{1:k})\propto P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1})$$
即：后验正比于似然乘先验。
其中，先验指前$k-1$帧的观测。根据马尔科夫假设，对先验展开得：
$$P(x_k|x_0,u_{1:k},z_{1:k-1})=\int P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})d{x}_{k-1}$$
即：$x_k$受$x_{k-1}$影响，考虑所有$k-1$时刻的$x$可能，对每一种可能，其概率是$x_{k-1}$下$x_k$的概率，乘以$x_{k-1}$的概率。
问题的最终目标是：求状态变量的最大后验概率形式。

二、 卡尔曼滤波器

1. 线性系统和卡尔曼滤波器(KF)

根据马尔科夫性，当前时刻状态只和上一时刻有关。我们来化简先验概率部分，把这个公式挪下来：
$$P(x_k|x_0,u_{1:k},z_{1:k-1})=\int P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})d{x}_{k-1}$$
等式右边第一项可以化简为：
$$P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})=P(x_k|x_{k-1},u_k)$$
第二项化简为：
$$P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})=P(x_{k-1}|x_0,u_{1:k-1},z_{1:k-1})$$
我对这两个式子化简的理解是：第一个是在$k-1$时刻状态$x_{k-1}$的条件下，得到$k$时刻状态$x_k$的概率。因为马尔可夫性，所以与$x_0$无关。但是去掉$z_{k-1}$并不理解。是指它是基于状态的概率，因此与观测无关吗？ 这可以看做运动方程。
第二个式子是$x_{k-1}$的概率，不涉及马尔可夫性，如$x_{k-2}$的条件，因此只讲发生在其后的$u_k$去掉。这可以看做上一帧的状态分布。
因此所做的事情是，根据上一时刻的状态分布，根据运动方程，二者结合得到当前时刻的先验，进而得到这一时刻的状态分布（后验）。

1.1. 线性高斯系统

使用线性方程描述运动方程和观测方程：
$$x_k=A_k{x}_{k-1}+u_k+w_k$$
$$z_k=C_k{x}_k+v_k$$
这个很好理解，$A,C$是转移矩阵，$u,z$是运动数据和观测数据，$w,v$是噪声。
输入是$x_{k-1}$的后验，根据它求$x_k$的先验，再求$x_k$的后验，作为这一步的最终结果。
因为高斯分布，均值代表了其状态估计值，协方差代表了其不确定性。
使用$x_k$表示待求的随机变量，${\hat{x}}_k$为其后验，${\overline{x}}_k$为其先验。

• 先验：$N({\overline{x}}_k,{\overline{P}}_k)$
• 似然：$N(C_k{x}_k,Q)$
• 后验：$N({\hat{x}}_k,{\hat{P}}_k)$

1.2. 卡尔曼滤波器(KF)

已知的是先验和似然的分布表示，$N({\overline{x}}_k,{\overline{P}}_k)$与$N(C_k{x}_k,Q)$。同时已知后验与先验、似然的关系：$N({\hat{x}}_k,{\hat{P}}_k)$=$N({\overline{x}}_k,{\overline{P}}_k)\times N(C_k{x}_k,Q)$，要求后验的概率分布表达式。
根据高斯分布指数项系数配方可求得。

KF分为以下几步，(ﾉ*･ω･)ﾉ可得：

1. 预测
   根据$k-1$时的$x$的后验，计算$k$时$x$的先验和似然。
   推导得到先验的均值和协方差：
   $${\overline{x}}_k=A_k{\hat{x}}_{k-1}+u_k,{\overline{P}}_k=A_k{\hat{P}}_{k-1}{A}_k^T+R$$
2. 更新
   求卡尔曼增益：
   $$K={\overline{P}}_k{C}_k^T(C_k{\overline{P}}_k{C}_k^T+Q{)}^{-1}$$
   更新后验：
   $${\hat{x}}_k={\overline{x}}_k+K(z_k-C_k{\overline{x}}_k),{\hat{P}}_k=(I-K{C}_k){\overline{P}}_k$$

卡尔曼滤波器依据线性系统，没有近似，是线性最优无偏估计。

2. 非线性系统和扩展卡尔曼滤波器(EKF)

实际SLAM系统存在问题：

• 运动方程和观测方程非线性
• 高斯分布经非线性变换后，不再是高斯分布

因此需要进行近似，将非高斯分布近似成高斯分布。 在非线性系统中的KF即为EKF。其做法是：在某个点附近考虑运动方程和观测方程的 一阶泰勒展开，即其线性部分，然后按照KF进行(ﾉ*･ω･)ﾉ。

2.1. 线性化

k时刻，把运动方程($f$)，观测方程($h$)，在${\hat{x}}_{k-1},{\hat{P}}_{k-1}$处线性化，即求在此处的偏导。
得到：
$$F=\frac{\partial f}{\partial x_{k-1}}{|}_{{\hat{x}}_{k-1}}$$
$$H=\frac{\partial h}{\partial x_k}{|}_{{\overline{x}}_k}$$

2.2. 扩展卡尔曼滤波器(EKF)

同样，分为两步：

1. 预测
   根据${\hat{x}}_{k-1}$，即上时刻后验，求出此时刻先验的概率分布形式（均值和协方差）。
   $${\overline{x}}_k=f({\hat{x}}_{k-1},u_k),{\overline{P}}_k=F{\hat{P}}_{k-1}{F}^T+R_k$$
2. 更新
   根据先验，求出卡尔曼增益，再求出后验。
   $$K_k={\overline{P}}_k{H}^T(H{\overline{P}}_k{H}^T+Q_k{)}^{-1}$$
   $${\hat{x}}_k={\overline{x}}_k+K_k(z_k-h({\overline{x}}_k)),{\hat{P}}_k=(I-K_{k}H){\overline{P}}_k$$

与KF对比，EKF可以看做在其基础上的改动：

• 将转移矩阵对变量的操作($C_k{x}_k$)，改为转移函数操作(h(x_k))。
• 将转移矩阵($A,C$)，改为转移函数的偏导值($F,H$)。

EKF给出的是，非线性系统单次线性近似的最大后验估计。

3. 局限

1. 马尔可夫性的局限
2. 一阶近似的局限
3. 需要存储均值和方差，因为路标量很大，因此协方差矩阵很大。

三、 BA与图优化

BA(Bundle Adjustment)：通过重投影不断优化估计的参数。
由于其稀疏属性，能够实现在线运行。

1. 投影模型和BA代价函数

此流程图即相机投影模型，也是观测方程的过程。注意，一个位姿只能观测到部分路标点。
观测方程：$$z=h(x,y)$$
其中：

• $z$: 像素坐标$(u_s,v_s{)}^T$
• $x$: 相机位姿，外参$R,t$，对应李代数$ϵ$
• $y$: 三维坐标点$p$

误差定义为：
$$e=z-h(ϵ,p)$$
代价函数：
$$\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\Vert e_{i,j}{\Vert }^2=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\Vert z-h(ϵ,p){\Vert }^2$$
即对所有的位姿和路标点组合下的观测误差求最小二乘。
对此最小二乘求解，相当于对位姿和路标同时调整，即BA。

2. BA的求解

自变量$x$是所有待优化的变量，包括所有位姿和所有路标点（为了方便把位姿的李代数记成$e$）。
$$x=[e_1,...,e_m,p1,...,p_n{]}^T=[x_c,x_p]$$
$$x_c=[e_1,...,e_m]T，六自由度$$
$$x_p=[p_1,...,p_n]T，三自由度$$
根据非线性优化，从初值开始，不断找增量$\delta x$，使最小二乘误差下降。
目标函数：
$$\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\Vert f(x+\delta x){\Vert }^2=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^n\Vert e_{i,j}+F_{i,j}\delta e_i+E_{i,j}\delta p_j{\Vert }^2$$
其中$F_{i,j}$是代价函数在当前状态下对相机姿态的偏导，$E_{i,j}$是代价函数在当前状态下对路标位姿的偏导。

雅克比矩阵由这两者构成：
$$J=[FE]$$
在G-N方法下，$H$矩阵为：
$$H=J^{T}J=\left[\begin{array}{cc}{F}^{T}F& F^{T}E\\ E^{T}F& E^{T}E\end{array}\right]=\left[\begin{array}{cc}{H}_{1,1}& H_{1,2}\\ H_{2,1}& H_{2,2}\end{array}\right]$$

3. 稀疏性

考虑$e_{i,j}$，为相机位姿$e_i$下看到的路标$p_j$的误差，其雅克比为：
$$J_{i,j}(x)=(0_{2\ast 6},...,0_{2\ast 6},\frac{\partial e_{i,j}}{\partial e_i},0_{2\ast 6},...,0_{2\ast 3},...,0_{2\ast 3},\frac{\partial e_{i,j}}{\partial p_j},0_{2\ast 6},...,0_{2\ast 6})=$$
可见，这个$J_{i,j}$是由好多2x6和2x3的块组成的，并且只有第$i$个2x6的块，和第$j$个2*3的块是不为零的。它们对应着相机位姿$e_i$和路标$p_j$的偏导。
对应到$H$，只有$(i,i),(i,j),(j,i),(j,j)$四个位置的块不为零。

因此整个$H$可以分块，并拥有以下性质：

• $H_{1,1}$是对角阵，在$H_{i,i}$处是非零块。
• $H_{2,2}$是对角阵，在$H_{j,j}$处是非零块。
• $H_{1,2}$和$H_{2,1}$的稀疏性不确定。

下面是一个更加直观表示其形状的图：
对于如下的位姿和路标关系：

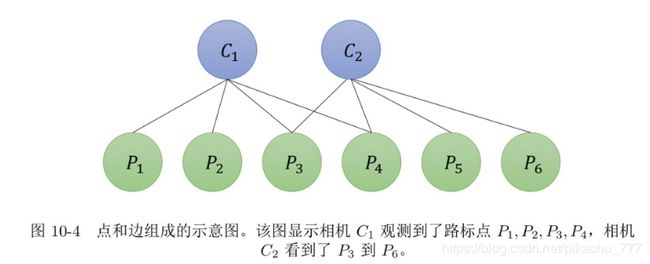
其$J,H$形状为：


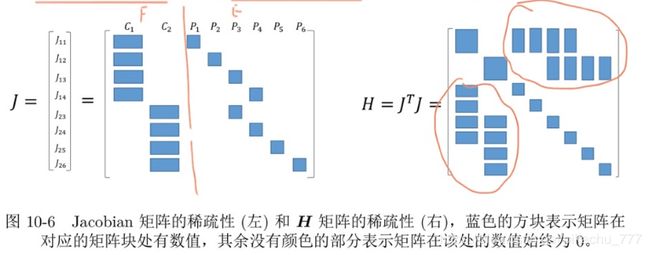
可见，$H_{1,2}$，$H_{2,1}$两部分的分布，和位姿与路标的邻接矩阵分布一致。

H矩阵的稀疏性质

其稀疏性可总结如下：

1. 左上角$B$为对角块矩阵，每个对角块元素维度与相机位姿维度相等(一般为6)。
2. 右下角$C$也是对角块矩阵，每个对角块元素维度与路标点维度相等(一般为3)。
3. 左下$E$和右上$E^T$两块，结构与观测数据相关。
4. 当路标点数量很大时，$B$很小，$C$很大，$E$和$E^T$零散分布。

4. 边缘化

拥有$H$后，目标是求解$H\delta x=g$。
$$\left[\begin{array}{cc}B& E\\ E^T& C\end{array}\right]\left[\begin{array}{c}\delta x_c\\ \delta x_p\end{array}\right]=\left[\begin{array}{c}v\\ w\end{array}\right]$$
使用边缘化方法消元：

1. 消去$E$，这样$H$矩阵的第一行就与$E$无关
2. 进而第一行乘后的结果，与$\delta x_p$无关，这样就可以解出$\delta x_c$。
3. 把$\delta x_c$带入，解出$\delta x_p$。

其中，主要计算两在于第二步。第三步中，由于$C$是对角块，其逆易求，因此在计算过程中计算量减少。

此外，第二步消元后的方程系数记做$S$，其稀疏性的意义为：非对角线上的非零矩阵块，表示了该出对应的两个相机变量之间存在着共同观测的路标点，称为共视。

从概率角度看，边缘化的意义是，先求了$x_c$的边缘概率。
$$P(x_c,x_p)=P(x_c)P(x_p|x_c)$$

四、代码解读

1. g2o

g2o_bundle.cpp

包含程序入口，图的创建，优化参数的设置和优化流程。
SolveProblem流程：

1. BundleParams params(argc,argv)读入并解析command参数。
2. BALProblem bal_problem(filename)读入数据，包括：

• 相机、路标、观测数
• 观测数据（相机-路标对，还有两个参数不知道是啥）
• 相机和路标的初始值

3. WriteToPLYFile存储原点云模型
4. 对初值添加噪声
5. 建立优化问题具体形式，包括：

• SetSolverOptionsFromFlags根据参数选择优化方法
• BuildProblem创建节点，包括相机位姿节点和路标节点
• BuildProblem创建边，为观测

6. 进行优化
7. WriteToBALProblem存储优化后的新数据
8. WriteToPLYFile存储优化后的点云模型

BALProblem

定义优化问题和图的参数，存储数据，实现了数据噪声添加、数据存储的功能。

g2o_bal_class.h

重写边和节点。包含：

1. 9自由度的相机节点
2. 3自由度的路标节点
3. 边，定义代价函数、J矩阵。

2. ceres

和g2o流程一致，只是在solver部分不同，自己定义了损失函数。
另外代码有bug，直接运行存储的点云名字是final_ply…，应该改成final.ply