二叉搜索树的节点插入，查找。

在讲解二分搜索树之前，我想先讲清楚一个东西，那就是递归，因为在后面的插入，查找操作都是利用递归去查找的，而且对于递归的理解也是一个难点，因此，以下是我对于递归的理解。

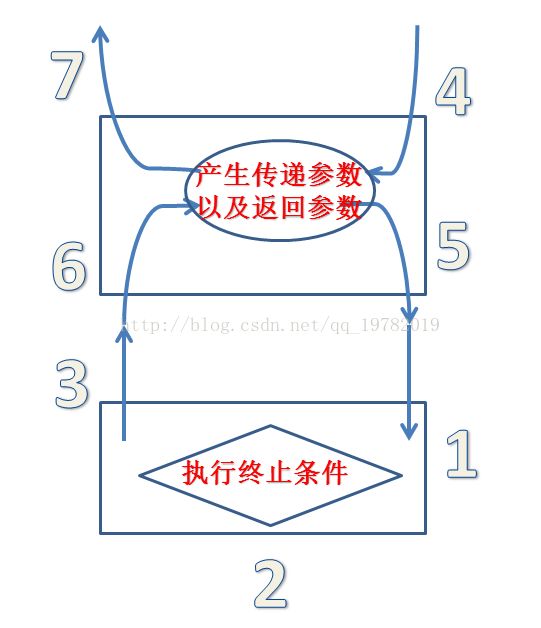
，对于递归，我们不能用人脑去展开来想，所以，我们只需要把递归过程中的两个过程给想清楚就好了，一个是递归发生在终止条件的时候，还有一个是递归在不断缩小规模的过程中其中的一个情况，具体我们可以见下图：

我们把最下面的方框理解为递归的出口，也就是递归发生终止时的情况，而上面的方框，我们理解为在终止条件发生前的前一个情况，因为一个人递归操作就是由这两种情况组成的，因此，我们只需要理清上面的两种情况就能够很好的理解递归了。

对于涉及到递归的问题，我们可以按照上图的思路来写出递归函数。

1.对终止条件进行判断  if(终止条件成立）

2.如果有必要的话，对传入的参数改造，或者自己产生参数

3.把我们产生的目标参数返回给上一层

4.接受来自上上层传递过来的参数

5.对传递过来的参数进行改造，把目标参数发往下一层级

6.接受下一层级往上传过来的目标参数，有必要的话对其利用或者改造。

7.把目标参数（需要返回的参数）发往上一层。

理解了上面的7点后，对于下面的递归操作就不难理解了。

我们首先来看看往二叉树中插入节点的方法：

// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    Node* insert(Node *node, Key key, Value value){

        if( node == NULL ){
            count ++;
            return new Node(key, value);
        }

        if( key == node->key )
            node->value = value;
        else if( key < node->key )
            node->left = insert( node->left , key, value);
        else    // key > node->key
            node->right = insert( node->right, key, value);

        return node;
    }
};

第一点： 对终止条件进行判断  if(终止条件成立）。

if( node == NULL )

第二点：如果有必要的话，对传入的参数改造，或者自己产生参数。

newNode(key, value)

第三点：把我们产生的目标参数返回给上一层。

returnnewNode(key, value);

第四点：接受来自上上层传递过来的参数。

Node *node, Key key, Value value

第五点：对传递过来的参数进行改造，把目标参数发往下一层级。

insert( node->left , key, value);

insert( node->right, key, value)

第六点：接受下一层级往上传过来的目标参数，有必要的话对其利用或者改造。

node->left = insert( node->left , key, value);

node->right = insert( node->right, key, value);

第七点：把目标参数（需要返回的参数）发往上一层。

return node;

根据以上的分析，我们发现递归函数大多符合上面的七点，因此我们只要按照上面的7

点为根本，然后再加上一些额外的操作，则一个递归函数差不多就写好了。

二叉树的查找（查找二叉树中是否存在某个key）：

 // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    bool contain(Node* node, Key key){

        if( node == NULL )
            return false;

        if( key == node->key )
            return true;
        else if( key < node->key )
            return contain( node->left , key );
        else // key > node->key
            return contain( node->right , key );
    }

二叉搜索树的查找（查找树中key相对应的value）：

 // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    Value* search(Node* node, Key key){

        if( node == NULL )
            return NULL;

        if( key == node->key )
            return &(node->value);
        else if( key < node->key )
            return search( node->left , key );
        else // key > node->key
            return search( node->right, key );
    }
};