对深搜的理解

深度优先搜索，顾名思义就是一条路走到头的搜索，今天俺来描述一下我对深搜的认识过程

首先我们po一个洛谷上的题：

题目背景
给定一个N*M方格的迷宫，迷宫里有T处障碍，障碍处不可通过。给定起点坐标和终点坐标，问: 每个方格最多经过1次，有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

输入格式
第一行N、M和T，N为行，M为列，T为障碍总数。第二行起点坐标SX,SY，终点坐标FX,FY。接下来T行，每行为障碍点的坐标。

输出格式
给定起点坐标和终点坐标，问每个方格最多经过1次，从起点坐标到终点坐标的方案总数。

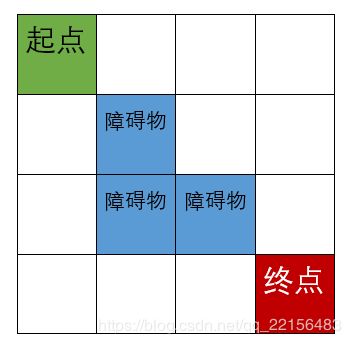
给一个简单的数据我们先来分析一下
4 4 3
1 1 4 4
2 2
3 2
3 3

好像不是很直观哈哈，给整个图，就这个亚子叭：

再给整个编号

我们先规定，到每个新节点，按右，下，上，左的顺序尝试；那么我们一步一步分析；

先放个流程图，哈哈哈

向右

向右

向下

向右

向下

向下

向右

向下

向下

向下

向下

向右

向右

向右

1

2

3

5

4

7

8

12

16

9

13

14

15

16

---

要完成上面的步骤，我们可以这样：

1. 每到一个节点按右下左上的顺序尝试，能走通就往下走，走完再回来走别的方向
2. 走过的结点不再走
3. 到终点就让计数器++，然后往回退一步并删除标记，再看上一个节点其他方向能否走通

---

介绍到这里就结束了，其实深搜也可以当作模拟来看，上面的步骤已经给了，下面放代码

#include
int a[100][100],book[100][100],n,m;
int ex,ey;
int flag=0;
int next[4][2]{{0,1},{1,0},{0,-1},{-1,0}};
void dfs(int x,int y);
int main()
{	
	int i,sd,aa,bb,sx,sy;
	scanf("%d%d%d",&n,&m,&sd);
	scanf("%d%d",&sx,&sy);
	scanf("%d%d",&ex,&ey);
	for(i=0;i<sd;i++)
	{
		scanf("%d%d",&aa,&bb);
		a[aa][bb]=1;
	}
	book[sx][sy]=1;
	dfs(sx,sy);
	printf("%d",flag);
	return 0;
}
//   dfs函数就是深搜的递归过程
void dfs(int x,int y)
{
	if(x==ex&&y==ey)	//结束条件，当走到终点计数器++并返回上一个步骤
	{
		flag++;
		return;
	}
	int i,tx,ty;
	for(i=0;i<4;i++)				//遍历四个方向
	{
		tx=x+next[i][0];ty=y+next[i][1];		//尝试过程
		if(tx<1||ty<1||tx>n||ty>m)				//判断能否走通（越界）
		{	
			continue;
		}
		if(a[tx][ty]==0&&book[tx][ty]==0)		//判断能否走通*2
		{
			book[tx][ty]=1;				//能走通，先标记，防止重复走
			dfs(tx,ty);
			book[tx][ty]=0;				//这里已经是从上一个节点返回了，所以删						        
										//除上一个tx，ty的标记
		}
	}
	return ;
}