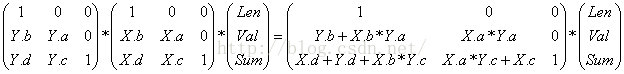【BZOJ4540】【Hnoi2016】序列 线段树
Claris劲啊！CA劲啊！
%%%两位线段树做法传送门在这里和这里
逆向题解时间到：
首先将询问按照终点排序，并且一边从
到
遍历，不妨设当前遍历到了点
，对于之前的每个点
，我们维护两个值
和
。(之后的点的两个值都先设成0)
其中
表示从这个点到之间序列A的最小值，而
，表示从我们遍历第一个点到当前的所有时刻下的各个历史版本的和。（当遍历的点在这个点之前等于零）（事实上
。）
不（很）难发现对于每一个询问
，当且仅当
时，有
。因为
也就是说，如果我们把询问全部离线下来，遍历的时候可以快速更新并且求和，，我们就可以快速回答每一个询问。
剩下就是线段树的锅了，我们把对于每个点的定义拓展到线段树的区间上，对于每个点以及它代表的
。
，，我们维护四个下传标记a,b,c,d，更新的时候
，初始化时a=1，b=c=d=0.
每加入一个值
，从这个数左边第一个大于它的数的位置+1到这个数的位置这一段的最小值都会被刷成，对应参数
同时我们要向加入最新版的的值，对应参数
。
两个下传标记打到一起时的处理方法来自于矩阵乘法。（图有毒，警告）
/**************************************************************
Problem: 4540
User: RicardoWang
Language: C++
Result: Accepted
Time:5196 ms
Memory:14948 kb
****************************************************************/
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define MAXN 100005
int size;
void _read(int &x)
{
char ch=getchar(); bool flag=false; x=0;
while(ch<'0' || ch>'9'){if(ch=='-')flag=true; ch=getchar();}
while(ch>='0' && ch<='9'){x=x*10+ch-'0'; ch=getchar();} if(flag)x=-x; return ;
}
struct q
{
int a,b,id;
}Q[MAXN];
int N,M,A[MAXN];
bool cmp(q x,q y)
{
return x.b>1;
build(chi[now][0],L,m); build(chi[now][1],m+1,R) ;return ;
}
void add(int now,int L,int R,node p)
{
long long len=R-L+1;
sum[now]+=p.c*val[now]+p.d*len;
val[now]=p.a*val[now]+p.b*len;
w[now]=w[now]+p;
return ;
}
void push_down(int now,int L,int R)
{
int m=(L+R)>>1;
node t=w[now];
if(t.a!=1 || t.b || t.c || t.d)
{
add(chi[now][0],L,m,t); add(chi[now][1],m+1,R,t);
w[now].clear();
}
return ;
}
node tmp;
void update(int now,int L,int R,int x,int y)
{
if(x<=L && R<=y){add(now,L,R,tmp);return ;}
int m=(L+R)>>1;push_down(now,L,R);
if(x<=m)update(chi[now][0],L,m,x,y);
if(y>m)update(chi[now][1],m+1,R,x,y);
sum[now]=sum[chi[now][0]]+sum[chi[now][1]]; val[now]=val[chi[now][0]]+val[chi[now][1]]; return ;
}
long long query(int now,int L,int R,int x,int y)
{
if(x<=L && R<=y)return sum[now];
int m=(L+R)>>1;push_down(now,L,R);
if(y<=m) return query(chi[now][0],L,m,x,y);
else if(x>m)return query(chi[now][1],m+1,R,x,y);
else return query(chi[now][0],L,m,x,y)+query(chi[now][1],m+1,R,x,y);
}
int st[MAXN],top;
long long ans[MAXN];
char s[55];int cct;
void out(long long x)
{
if(!x)putchar('0');
if(x<0)putchar('-'),x=-x;
cct=0;while(x){cct++; s[cct]=x%10+'0'; x=x/10;}
while(cct){putchar(s[cct]); cct--;}
putchar('\n');
}
void work()
{
build(rt,1,N);
top=0;int j=1;
for(int i=1;i<=N;i++)
{
while(top&& A[st[top]]>=A[i])top--;
tmp=(node){0,A[i],0,0}; update(rt,1,N,st[top]+1,i);
add(1,1,N,(node){1,0,1,0}); st[++top]=i;
while(j<=M && Q[j].b==i) {ans[Q[j].id]=query(rt,1,N,Q[j].a,Q[j].b);j++;}
}
for(int i=1;i<=M;i++)out(ans[i]);
//out(0); out(-0); out(-123);out(1234);
return ;
}
int main()
{
//freopen("in.txt","r",stdin);
Init();
work();
return 0;
} （然而全程LL还不如莫队快）