(二十一)论文阅读 | 目标检测之Dynamic RCNN
简介
本文介绍的是 2020 2020 2020年的一篇关于目标检测的论文, D y n a m i c R { \rm Dynamic\ R} Dynamic R- C N N {\rm CNN} CNN。由它的名字我们可以初步得到,它也是 R {\rm R} R- C N N {\rm CNN} CNN系列算法,即两阶段目标检测算法;然后动态性其实体现在在训练目标检测模型过程中使用动态训练的策略。前面介绍过的 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN也可以看作是一种动态训练方法,它在训练过程中不断调整交并比阈值的大小以提高候选框的质量。而论文在训练过程中不仅关注了交并比阈值的动态设置,也在自适应地调整回归损失的形式。实验结果为在 M O C O C O {\rm MO\ COCO} MO COCO数据集上相比于 S O T A {\rm SOTA} SOTA方法的 A P {\rm AP} AP提高了 1.7 % {\rm 1.7\%} 1.7%。论文原文 源码
0. Abstract
作者首先指出,尽管两阶段目标检测算法的模型精度持续占据着金字塔顶,但这类模型的训练过程可以得到改善。首先,动态训练的方法与模型的固定设置之间存在着不一致。如在训练过程中正负样本的分配策略以及回归损失函数形式不能随着样本总体特征的变化而变化。针对以上两点,论文提出的 D y n a m i c R { \rm Dynamic\ R} Dynamic R- C N N {\rm CNN} CNN用于缓解上述问题。
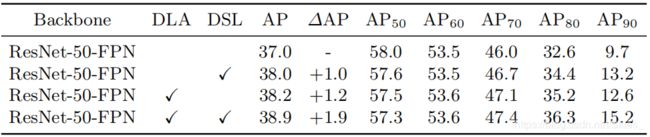
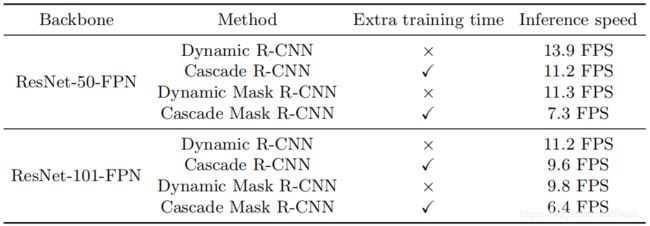
论文贡献:(一)基于目标检测的训练特征,指出应该基于样本分布的变化而动态调整训练的策略;(二)提出 D L A {\rm DLA} DLA和 D S L {\rm DSL} DSL的训练方法,其仅通过引入两个变量就可以实现;(三)引入该方法在提高性能的同时不会降低模型的速度。
1. Introduction
在引言部分文章首先指出,不同于图像分类里的分类概念,目标检测中的分类是基于标注框进行的。即与图像分类中每幅图像都有明确的类别标签不一样,在目标检测中不存在绝对的准则判断该候选框属于正类还是负类。而在目标检测中常用的用于确定正负样本的方法是设定交并比阈值,如果先验框框与标注框的交并比在某个范围内,则认定其为正样本,否则为负样本。但在训练过程中设定固定的阈值往往不能获得最佳的结果, C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的解决办法是不断加大阈值,从而不断提高候选框的质量,但这其实是一个级联的检测过程,会引入大量的计算。同时,在边界框的回归过程也存在以上问题。
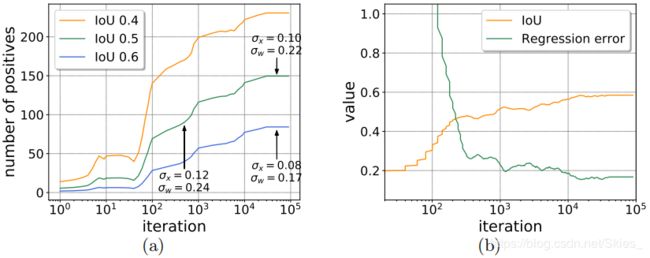
由图 2 2 2中的 ( a ) {\rm (a)} (a)可知,无论交并比阈值设置为多少,随着迭代次数的增加,正样本数量都在急剧增加(这是由于随着训练的进行,模型对样本的分类能力增强);图 2 2 2中的 ( b ) {\rm (b)} (b)展示的回归情况也是如此。
2. Related Work
相关工作部分文章首先简要介绍了 R {\rm R} R- C N N {\rm CNN} CNN系列方法,然后指出目标检测中常用到的分类方法以及边界框回归方法。在这几个部分中,作者均提到了对 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的参考。最后介绍了模型的学习方法,如课程学习和自步学习等。二者的策略均是模仿人类的学习方法,即先从简单的事物开始学起以找到有效的学习方式,进而聚焦于对复杂样本的学习。
3. Dynamic Quality in the Training Procedure
3.1 Proposal Classification
在目标检测中正负样本的区分策略一直是人们研究的热点,直观上我们认为如果预测框与任何标注框均不相交则视为负样本,如果与某个标注框完全重叠则视为正样本,但如果其和标注框的 I o U {\rm IoU} IoU为 0.5 {\rm 0.5} 0.5时则没有绝对的界定方法。 F a s t e r R {\rm Faster\ R} Faster R- C N N {\rm CNN} CNN中区分正负样本的策略如下: l a b e l = { p o s i t i v e i f m a x I o U ( b , G ) ≥ T + n e g a t i v e i f m a x I o U ( b , G ) < T − i g n o r e d o t h e r w i s e (1) {\rm label=}\left\{ \begin{aligned} &positive&&{\rm if}\ {\rm max}\ IoU(b,G)≥T_{+}\\ &negative&&{\rm if}\ {\rm max}\ IoU(b,G)<T_{-}\\ &ignored&&{\rm otherwise}\\ \end{aligned} \right.\tag{1} label=⎩⎪⎨⎪⎧positivenegativeignoredif max IoU(b,G)≥T+if max IoU(b,G)<T−otherwise(1)
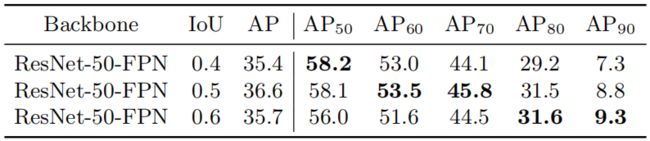
F a s t e r R {\rm Faster\ R} Faster R- C N N {\rm CNN} CNN中主要通过人为设定的正负样本阈值来区分,这也是现在常用的分配方案。由于分类器的目的是产生正负样本,所以不同的交并比阈值也会产生不同的分类效果。相关实验结果如下:
由上图可知,不同指标的最佳结果并没有在同一设定的 I o U {\rm IoU} IoU阈值处,我们理想的结果就是通过某种方法可以在不同检测标准下均得到最佳结果。 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN中通过级联的方式不断增大 I o U {\rm IoU} IoU阈值,从而得到了最佳的效果,但这种方法同时也引入大量额外的计算。直观上,在训练的初始阶段,模型并不能产生大量的高质量样本,这时应设置较低的 I o U {\rm IoU} IoU阈值以获得足够数量的正样本;随着训练过程的推移,这时应该适当增加 I o U {\rm IoU} IoU阈值以获得高质量的样本来训练模型。文章提出了不同于 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的方法,后文会介绍。
3.2 Bounding Box Regression
在目标检测中边界框回归的方式通常遵循的是 F a s t e r R {\rm Faster\ R} Faster R- C N N {\rm CNN} CNN中的策略,如下: δ x = ( g x − b x ) / b w , δ y = ( g y − b y ) / b h δ_x=(g_{x}-b_{x})/b_w,\ \ δ_y=(g_{y}-b{y})/b_h δx=(gx−bx)/bw, δy=(gy−by)/bh
δ w = l o g ( g w / b w ) , δ h = l o g ( g h / b h ) (2) δ_w={\rm log}(g_w/b_w),\ \ δ_h={\rm log}(g_h/b_h)\tag{2} δw=log(gw/bw), δh=log(gh/bh)(2)
其中 δ δ δ是预测框相对于标注框的偏移大小,通常会将其归一化以稳定训练过程。但作者通过实验发现,随着训练的进行,回归目标的分布(即均值和和方差)在不断变化,如下图:
由上图的第一列和第二列可知,两组实验是设定的相同 I o U {\rm IoU} IoU阈值。随着训练过程的进行,模型产生更多高质量的样本,造成回归目标的均值和方差均减小。根据 S m o o t h L 1 {\rm SmoothL1} SmoothL1损失函数的形式,这会降低正样本在训练模型时的贡献(由于均值和方差均减小,预测的偏移也会减小即损失值减小,而此时正样本的比例是在不断变大的。即相对减小了高质量的正样本在训练过程中的贡献),从而限制了模型的整体性能。因此,有必要根据样本的分布对损失函数的形式动态地进行调整。
4. Dynamic R-CNN
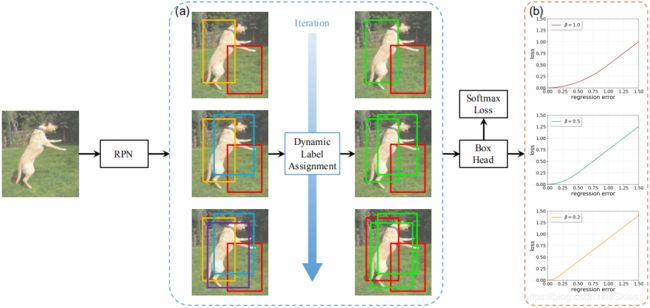
上图展示了 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN的整体流程,其核心思想是基于样本的分布动态地调整分类器和回归器。首先,输入图像经由 R P N {\rm RPN} RPN产生候选区域,由于随着训练过程的迭代而产生越来越多的高质量样本,这时增大 I o U {\rm IoU} IoU阈值。如 ( a ) {\rm (a)} (a)中右边的绿色框表示正样本,随着阈值的增加正样本的数量而不断增加。文中将这个过程称之为动态样本分配, D L A {\rm DLA} DLA。 ( b ) {\rm (b)} (b)中展示了不同 β \beta β的 S m o o t h L 1 {\rm SmoothL1} SmoothL1损失函数的变化情况,设置不同 β \beta β的即为文中提到的 D S L {\rm DSL} DSL方法。
4.1 Dynamic Label Assignment
l a b e l = { 1 i f m a x I o U ( b , G ) ≥ T n o w 0 i f m a x I o U ( b , G ) < T n o w (3) {\rm label=}\left\{ \begin{aligned} &1&&{\rm if}\ {\rm max}\ IoU(b,G)≥T_{now}\\ &0&&{\rm if}\ {\rm max}\ IoU(b,G)<T_{now}\\ \end{aligned} \right.\tag{3} label={10if max IoU(b,G)≥Tnowif max IoU(b,G)<Tnow(3)
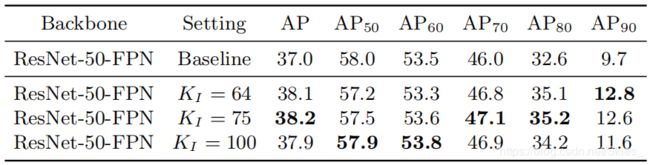
上式是 D L A {\rm DLA} DLA的形式,由经典 F a s t e r R {\rm Faster\ R} Faster R- C N N {\rm CNN} CNN中的形式得到,其中 T n o w T_{now} Tnow表示当前的 I o U {\rm IoU} IoU阈值。 I o U {\rm IoU} IoU的动态变化过程如下:首先计算候选框与其匹配的标注框的交并比 I I I,然后选择第 K I K_{I} KI大的值作为当前的 I o U {\rm IoU} IoU阈值 T n o w T_{now} Tnow。随着训练的过程, T n o w T_{now} Tnow会随着 I I I的增大而增大。在具体实践中,首先计算批次样本中的第 K I K_{I} KI大的 I o U {\rm IoU} IoU值,然后每 C C C个迭代使用前者的平均值更新 T n o w T_{now} Tnow(由于一次迭代会产生很多批次)。 D L A {\rm DLA} DLA的思路同 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN一致,只是选取阈值的方法有所不同。
4.2 Dynamic SmoothL1 Loss
S m o o t h L 1 {\rm SmoothL1} SmoothL1损失函数的形式如下: S m o o t h L 1 ( x , β ) = { 0.5 ∣ x ∣ 2 / β i f ∣ x ∣ < β ∣ x ∣ − 0.5 β o t h e r w i s e (4) {\rm SmoothL1}(x,\beta)=\left\{ \begin{aligned} &0.5|x|^2/\beta&&{\rm if}\ |x|<\beta\\ &|x|-0.5\beta&&otherwise\\ \end{aligned} \right.\tag{4} SmoothL1(x,β)={0.5∣x∣2/β∣x∣−0.5βif ∣x∣<βotherwise(4)
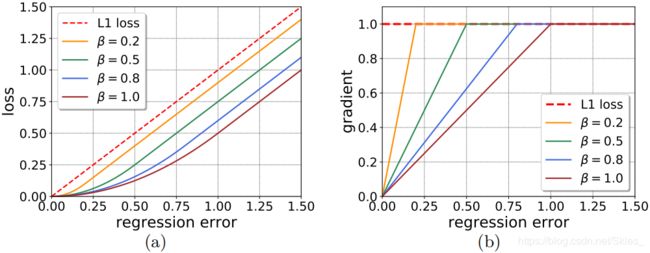
上图展示了 S m o o t h L 1 {\rm SmoothL1} SmoothL1损失函数的不同参数设置得到的损失和梯度变化情况。随着 β \beta β值的减小,梯度更快趋于饱和,从而使较小的误差对模型的训练有更大的贡献。(这里没有理解具体为什么会采取如下措施,结合后面损失函数的形式,可以理解为随着迭代训练的进行,增大回归部分的损失而适当加快模型训练)则回归损失函数的形式如下: S m o o t h L 1 ( x , β ) = { 0.5 ∣ x ∣ 2 / β n o w i f ∣ x ∣ < β n o w ∣ x ∣ − 0.5 β n o w o t h e r w i s e (5) {\rm SmoothL1}(x,\beta)=\left\{ \begin{aligned} &0.5|x|^2/\beta_{now}&&{\rm if}\ |x|<\beta_{now}\\ &|x|-0.5\beta_{now}&&otherwise\\ \end{aligned} \right.\tag{5} SmoothL1(x,β)={0.5∣x∣2/βnow∣x∣−0.5βnowif ∣x∣<βnowotherwise(5)
具体的做法是,首先候选框与其匹配的标注框的回归损失 E E E,然后选择第 K β K_{\beta} Kβ小的值作为当前 β \beta β值。在具体实践中,首先计算每批次样本中的第 K β K_{\beta} Kβ小的损失值,然后每 C C C个迭代使用前者的中间值更新 β \beta β。最后,给出 D y n a m i c R { \rm Dynamic\ R} Dynamic R- C N N {\rm CNN} CNN的总体检测流程,其中第八行和第九行分别是 D L A {\rm DLA} DLA和 D S A {\rm DSA} DSA的关键步骤。
5. Experiments
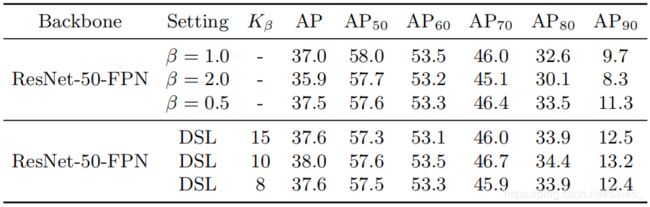
图上前面三行展示了不使用论文提出的 D S L {\rm DSL} DSL方法,后面三行为不同超参数下使用 D S L {\rm DSL} DSL的实验结果。可以看到,下面三行的结果普遍优于上面的结果。同时在 K β = 10 K_{\beta}=10 Kβ=10时,模型取得了最佳的结果。
6. Conclusion
论文以实验结果引入,得出在训练目标检测模型的过程中应随着样本的分布变化而动态设置分类器和回归器的结论。借鉴 C a s c a d e R {\rm Cascade\ R} Cascade R- C N N {\rm CNN} CNN中动态训练的设置,论文提出 D L A {\rm DLA} DLA在训练过程中动态改变交并比阈值以提高获取样本的质量。接着,借鉴 D L A {\rm DLA} DLA的思路,通过修改 S m o o t h L 1 {\rm SmoothL1} SmoothL1的参数动态调整回归器的形式,得到 D S L {\rm DSL} DSL。论文提出的方法在程序实现上并不困难,在定义分类器和回归器时分别引入一个变量即可。但是本文并没有理解文中的几个配图,是结合后续内容理解的。纵观全文,其创新性其实并不强,在 A T S S {\rm ATSS} ATSS中分析有框检测算法和无框就算法的异同后提出一种自适应的样本采样方法。本文可以借鉴的思路是,在训练目标检测器时应随着数据的变化而动态地改变训练的策略,文中给出了分类器和回归器两个方面。
参考
- Zhang H, Chang H, Ma B, et al. Dynamic R-CNN: Towards High Quality Object Detection via Dynamic Training[J]. arXiv preprint arXiv:2004.06002, 2020.