2017.10.29闵神讲课DAY2(数论)
模运算
等大家刷题刷的多了,就会发现一些题会要求你对最终答案对P取模(当然也会有一些**的题目会让你高精度,不谈了)
除法定理
对于一个整数x和正整数p,x能被唯一地表示为x=a*p+b,其中a是整数,b是小于p的非负数.
这个小学学过吧,a是x除以p的商,b是余数。
x对p取模的结果自然是b,如果有另一个数y=c*p+d,首先y模p的结果就是d,那么这两个数如果做一些运算答案对p取模的结果是什么呢?
下面推一些公式,不是很难。
加减乘…..
继续沿用刚才x和y的定义:
x±y=(a±b)p+(c±d),设c±d=e*p+f,那么
x±y=(a±b+e)p+f,所以(x±y)%p=(c±d)%p
x*y=(a*c)*p^2+(b*c+a*d)*p+(c*d),设c*d=e*p+f
那么xy=(a*c*p+b*c+a*d+e)*p+f,(xy)%p=(cd)%p
这个说明了什么呢?不管x和y本身是多少,他们运算后模p的结果就是他们模p后运算的结果再模p,求解时只需要保留过程中的数模p的结果就行
定义运算
有了这个性质我们就可以把程序中所有需要操作的数都限定到[0,p-1]范围内辣。
思考:如果数刚开始不是这个范围内咋办?
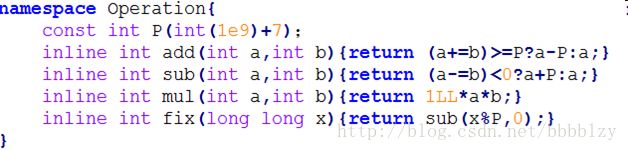
下面是闵神的模板,注意细节和常数的处理。
也就是举个例子
如果题目要你%2333(这是一个质数)
那么在这个题目中2334等价于1
4666等价于0
就是2334=1,,4666=0在此题是正确的
这样我们就可以避免很多大数据的计算
乘法逆元
在此我们需要引进两个新的概念:
单位元:单位元(英文常写作Identity Element,即IE)是集合里的一种特别的元,与该集合里的运算(可理解为实数里的*,但并不局限于)有关。当它和其他元素结合时,并不会改变那些元素。(说的通俗一点,加法的单位元就是0,;乘法的单位元就是1)
逆元:逆元素是指一个可以取消另一给定元素运算的元素,在数学里,逆元素广义化了加法中的加法逆元和乘法中的倒数。
对于除法来说,同余原理是不满足的(即(a/b)%p!=(a%p)/(b%p))
那么我们该怎么处理除法呢??
这时候我们就要用到逆元了!
将除法转化为乘这个数的逆元
定义:对于正整数a和m,如果a*x mod m=1, 则x的最小正整数解称为a模m的逆元,表示为a^(-1) (mod m)
求解方法:(1)根据费马小定理:有a^(m-1) mod m=1, 即a*a^(m-2) mod m=1, 所以a^(m-2)就是a模m的逆元。 (适用条件:m为素数)
(2)扩展欧几里得求解:a*x mod m=1,即a*x-m*y=1,解这个丢番图方程即可。 (适用条件:gcd(a,m)=1)
(3)欧拉函数法:留个坑。
(4)线性递推:规定m为质数,且1^(-1)≡1(mod m) 设 m=k∗a+b(b<a,1<a<m) , 即 k∗a+b≡0(mod m)
两边同时乘以a^(−1)∗b^(−1),得到:
k∗b(−1)+a(−1)≡0(modm)
a(−1)≡−k∗b(−1)(modm)
a(−1)≡−m/a∗(mmoda)(−1)(modm)
从头开始扫一遍即可,时间复杂度O(n) (适用条件:m为素数)
逆元的一个经典应用:我们知道除法不符合模性质,那么在解决(a/b)mod m 的问题时该怎么办呢?
推导一下:设a/b=k*m+x,那么x就是所求答案。
a=k∗m∗b+x∗b
amod(m∗b)=x∗b
x=(amod(m∗b))/b
但是如果b很大,则会出现爆精度问题,所以我们避免使用除法直接计算。
可以使用逆元将除法转换为乘法:
假设b存在乘法逆元,即与m互质(充要条件)。设c是b的逆元,即b∗c≡1(modm),那么有 a/b=(a/b)∗1=((a/b)∗b∗c)modm=(a∗c)modm
即,除以一个数取模等于乘以这个数的逆元取模。
同余原理求gcd
欧几里得算法:
gcd(a,b)=gcd(a,a-b)
我们根据同余原理可以进行优化
gcd(a,b)=gcd(a,a%b)
效率更高,算法更优秀
那么gcd的时间复杂度为多少???
让我们来想一想:b每次取模,至少减少到自己的一半,那么在最坏情况下,时间复杂度就是O(logb)
那么什么是最坏情况呢??
大家可以自己想一下…………..
斐波那契数列!!!!!
惊不惊喜 意不意外
大家来想一下
gcd(fn,fn-1)=??
gcd(fn,fn-1)=gcd(fn-1,fn-2)
显然时间复杂度就是O(logn)
扩展欧几里得算法
设xa+yb=d=gcd(a,b),其中x和y可能有很多对,我们的任务就是求出至少一对x和y。
根据欧几里得算法,xa+yb=d=x’(b)+y’(a % b )
最后一定有x’=1,y’=0,那么我们只需要在递归返回的时候通过x’和y’计算出x和y就行了。
a%b=a-a/b*b,那么d=y’a-(x’-a/b*y’)*b(/为整除)
待定系数就能求出x=y’,y=x’-a/b*y’。
大功告成,递归求gcd返回的同时递推一下就行
然后求出来这个x之后你把它fix一下就可以辣。
欧拉定理
不要以为扩展欧几里得很简单,还要更简单的!!!
若x和p互质,则x^euler(p) ≡1(mod p),其中euler(p)是比p小且与p互质的数的个数,称为欧拉函数。
于是乎x^(euler(p)-1)就是x的逆元了。
于是我们可以用倍增快速幂来求。
时间复杂度为O(logp),但是logp同时也是下界,所以可能会比扩欧慢一些,但是写起来方便。
为什么模数一般都是质数
一般来说题目中的模数P都以两种形式出现:1.给定的2.作为输入文件中的一个数出现。
第一种情况模数一般都是有特殊性质的,大部分情况下P是质数。
第二种情况一般都不保证是质数。
如果模数不是质数,意味着我们我们失去了除法这一强有力的运算,此时我们只有加减乘三种运算,所以要么抛弃除法,要么另寻他法。
Lucas定理
例题:给q个询问,每个询问求C(n,m)%p,n,m≤1e18,q≤1e5,p=2333。
不能用递推,不能用除法,但是模数很小诶。
C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)(p为质数)
于是我们只需要预处理出来n,m<2333的组合数然后递归求就可以了,O(p^2+qlogn)
关于这个定理,有一道很好的例题:BZOJ4591
中国剩余定理
若我们已知m个互不相同的模数pi(i=1…m)那么一个数模这几个数的余数(a1,a2,…,am)与这个数模这m个数P的乘积r存在一一对应关系。
设Mi=P/pi(整除),ti=Mi^-1(mod pi),那么
r=sum{ai*ti*Mi}%P
有了这个式子,我们就可以分别求出来答案模P的质因子的结果然后用这个式子将最终答案还原即可。
线性筛
不重不漏的意思是每个合数都被筛且仅筛了一遍。
首先用显然法证明每个合数一定都会被筛掉一次。
考虑每个合数会被哪些数通过乘上一个素数筛去。
x=p1^e1*p2^e2*…*pk^ek
假设它被素数pj筛去,那么我们可以发现,如果j不为1的话,那么筛掉它的那个数y在筛其他数的过程中会因为是p1的倍数而停止筛数,所以x不可能通过y*pj被筛掉,只能被某个z*p1筛掉,这样也就是只会被筛一次。
BSGS
问题:求满足a^x≡y(mod p)的最小的x,ap互质。
设x=im+j(0≤j<m)
那么a^(im)≡y*a^(-j)(mod p)
枚举j,将所有的y*a^(-j)放入哈希表中。
然后枚举i,在哈希表中查找a^(-im)是否存在。
第一个匹配的im+j是最小解(因为从小到大枚举i)。
BSGS是一个叫做meet-in-the-middle算法的实例。