python_numpy_方波的傅立叶分解

使用最小二乘法可以解决的问题之
将一个方波分解为
asin(x)+bsin(2x)+...+csin(nx)+dcos(x)+ecos(2x)+...+fcos(nx)

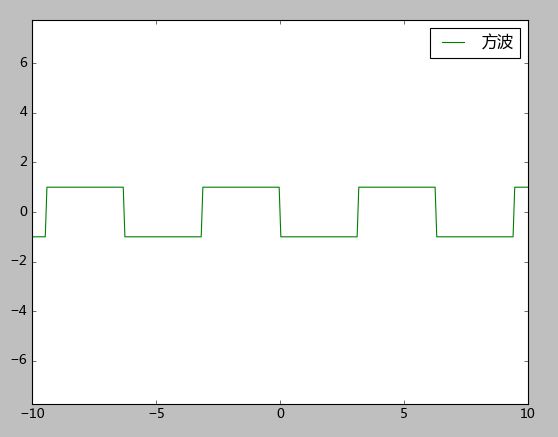
产生一个方波：
使用周期函数sin产生方波，sinx>0,y=-1,sinx<0,y=1

x = np.linspace(-10,10,300)
y=[]
for i in x:
    if np.sin(i)>0:#调用sin，cos要使用np.sin，np.cos
        y.append(-1)
    else:
        y.append(1)
y=np.array(y)#需要把list转化成array，方便进行矩阵的运算

方波

将一个方波分解为
asin(nx),bcon(nx)的线性组合，
如：
asin(x)+bsin(2x)+...+csin(nx)+dcos(x)+ecos(2x)+...+fcos(nx)
要求的是系数a，b...c,d...e,f组成的矩阵，输入量是方波（x，y）与n的值。
所以定义函数：

def fourier(x,y,n):
    return ym
#返回值为asin(nx),bcon(nx)的线性组合，
#即，系数a，b...c,d...e,f组成的矩阵与x1（sin(nx),con(nx)）的乘积

函数fourier

def fourier(x,y,n):
    x1=[]#（sin(nx),con(nx)）
    for i in xrange(n):
        x1.append(np.sin(x*i+x))
        x1.append(np.cos(x*i+x))
    m=np.mat(x1).T#使用np.mat方便矩阵的连乘
    y.shape=(y.shape[0],1)
    p=m*np.linalg.inv(m.T*m)*m.T*y
    ym=np.array(p)#将矩阵转换成array，与前面统一
    ym.shape=(ym.shape[0],)
    return ym

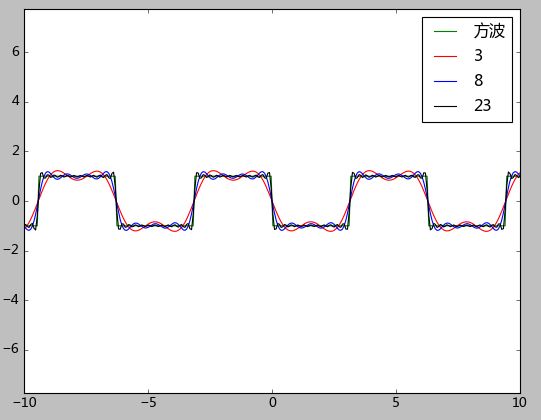
对比选择不同n值得分解结果：

plt.plot(x,y,color="g",label=u'方波')
plt.plot(x,fourier(x,y,3),color='r',label='3')
plt.plot(x,fourier(x,y,8),color='b',label='8')
plt.plot(x,fourier(x,y,23),color='k',label='23')
plt.legend()
plt.axis('equal')
plt.show()

Paste_Image.png

可以看出n值越大，分解后的函数越接近方波函数
完整程序：
http://pan.baidu.com/s/1ckHTYu
提取密码：kwrv