Kaggle案例泰坦尼克号问题

泰坦里克号预测生还人口问题

泰坦尼克号问题背景

- 就是那个大家都熟悉的『Jack and Rose』的故事，豪华游艇倒了，大家都惊恐逃生，可是救生艇#### 的数量有限，无法人人都有，副船长发话了lady and kid first!，所以是否获救其实并非随机，而是基#### 于一些背景有rank先后的。

- 训练和测试数据是一些乘客的个人信息以及存活状况，要尝试根据它生成合适的模型并预测其他人的存活状况。

一.数据预处理

import pandas as pd #数据分析
import numpy as np #科学计算
from pandas import Series,DataFrame
data_train = pd.read_csv("Train.csv")
data_train

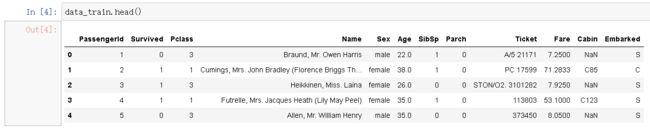
训练集

测试集

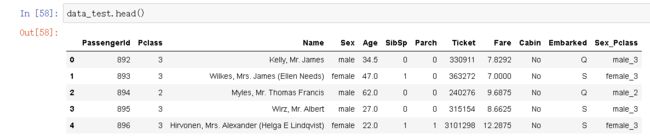
我们看到，总共有12列，其中Survived字段表示的是该乘客是否获救，其余都是乘客的个人信息，包括：

• PassengerId => 乘客ID
• Pclass => 乘客等级(1/2/3等舱位)
• Name => 乘客姓名
• Sex => 性别
• Age => 年龄
• SibSp => 堂兄弟/妹个数
• Parch => 父母与小孩个数
• Ticket => 船票信息
• Fare => 票价
• Cabin => 客舱
• Embarked => 登船港口

弄清楚数据集的数据条数和各列信息的完整性：

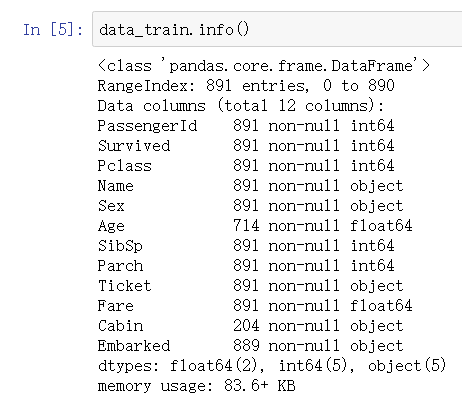
上面的数据告诉我们，训练数据中总共有891名乘客，但是很不幸，我们有些属性的数据不全，比如#### 说：Age（年龄）属性只有714名乘客有记录Cabin（客舱）更是只有204名乘客是已知的

了解数据集各列的统计信息（针对数值型数据）：

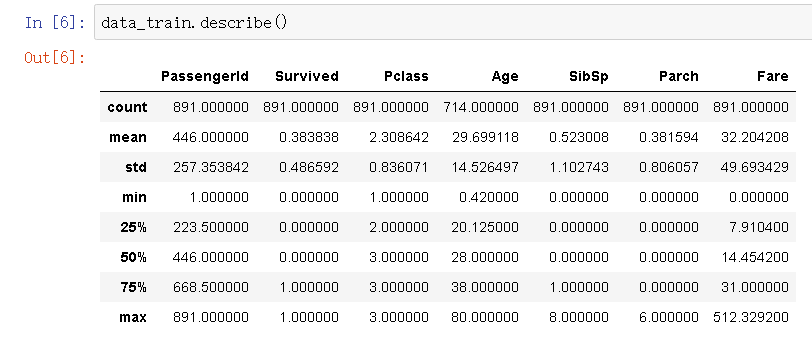
mean字段告诉我们，大概0.383838的人最后获救了，2/3等舱的人数比1等舱要多，平均乘客年龄大#### 概是29.7岁(计算这个时候会略掉无记录的)等等…

import matplotlib.pyplot as plt
fig = plt.figure()

from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']   # 雅黑字体
mpl.rcParams['axes.unicode_minus'] = False
fig.set(alpha=0.5)  # 设定图表颜色alpha参数
plt.subplot2grid((2,3),(0,0))             # 在一张大图里分列几个小图
data_train.Survived.value_counts().plot(kind='bar')# plots a bar graph of those who surived vs those who did not. 
plt.title(u"获救情况 (1为获救)") # puts a title on our graph
plt.ylabel(u"人数")  

plt.subplot2grid((2,3),(0,1))
data_train.Pclass.value_counts().plot(kind="bar")
plt.ylabel(u"人数")
plt.title(u"乘客等级分布")

plt.subplot2grid((2,3),(0,2))
plt.scatter(data_train.Survived, data_train.Age)
plt.ylabel(u"年龄")                         # sets the y axis lable
plt.grid(b=True, which='major', axis='y') # formats the grid line style of our graphs
plt.title(u"按年龄看获救分布 (1为获救)")

plt.subplot2grid((2,3),(1,0), colspan=2)
data_train.Age[data_train.Pclass == 1].plot(kind='kde')   # plots a kernel desnsity estimate of the subset of the 1st class passanges's age
data_train.Age[data_train.Pclass == 2].plot(kind='kde')#（核密度估计）
data_train.Age[data_train.Pclass == 3].plot(kind='kde')
plt.xlabel(u"年龄")# plots an axis lable
plt.ylabel(u"密度") 
plt.title(u"各等级的乘客年龄分布")
plt.legend((u'头等舱', u'2等舱',u'3等舱'),loc='best') # sets our legend for our graph.

plt.subplot2grid((2,3),(1,2))
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u"各登船口岸上船人数")
plt.ylabel(u"人数")  
plt.show()

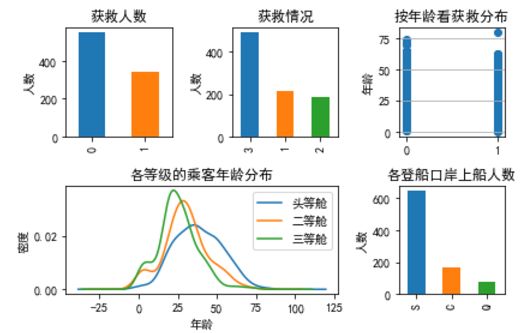
我们在图上可以看出来:被救的人300多点，不到半数；

3等舱乘客灰常多；遇难和获救的人年龄似乎跨度都很广；

3个不同的舱年龄总体趋势似乎也一致，2/3等舱乘客20岁多点的人最多，1等舱40岁左右的最多 (→_→似乎符合财富和年龄的分配哈，咳咳，别理我，我瞎扯的)；

登船港口人数按照S、C、Q递减，而且S远多于另外俩港口。

这个时候我们可能会有一些想法了：

不同舱位/乘客等级可能和财富/地位有关系，最后获救概率可能会不一样

年龄对获救概率也一定是有影响的，毕竟前面说了，副船长还说『小孩和女士先走』呢

和登船港口是不是有关系呢？也许登船港口不同，人的出身地位不同？

口说无凭，空想无益。老老实实再来统计统计，看看这些属性值的统计分布吧。

#看看各乘客等级的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  #设定图表颜色alpha参数

Survived_0 = data_train.Pclass[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Pclass[data_train.Survived == 1].value_counts()
df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)#多分类累积柱状图 Stacked Bar
plt.title(u"各乘客等级的获救情况")
plt.xlabel(u"乘客等级") 
plt.ylabel(u"人数") 

plt.show()

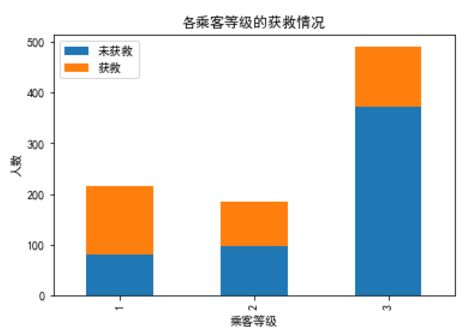
fig = plt.figure()
fig.set(alpha=0.5)

un_survived = data_train.Pclass[data_train.Survived == 0].value_counts()#未获救人的等级分布
# print(type(un_survived))#
survived = data_train.Pclass[data_train.Survived == 1].value_counts()#获救人的等级分布
df = pd.DataFrame({'未获救':un_survived,'获救':survived})
df.plot(kind = 'bar',stacked = True)
plt.show()

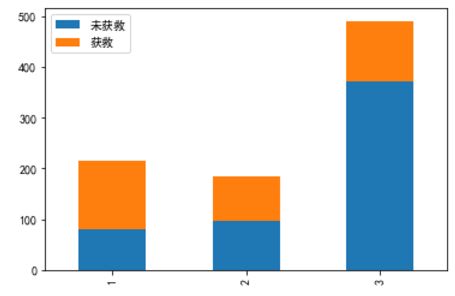
明显等级为1的乘客，获救的概率高很多。恩，这个一定是影响最后获救结果的一个特征。

#看看各登录港口的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  #设定图表颜色alpha参数

Survived_0 = data_train.Embarked[data_train.Survived == 0].value_counts()
Survived_1 = data_train.Embarked[data_train.Survived == 1].value_counts()
df=pd.DataFrame({u'获救':Survived_1, u'未获救':Survived_0})
df.plot(kind='bar', stacked=True)
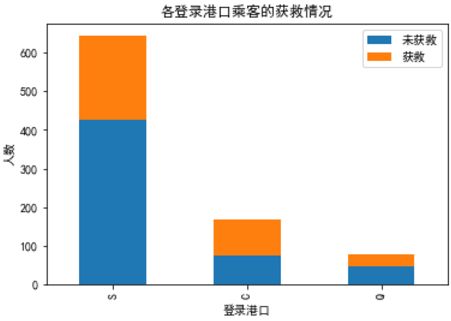
plt.title(u"各登录港口乘客的获救情况")
plt.xlabel(u"登录港口") 
plt.ylabel(u"人数") 
plt.show()

# 看看各性别的获救情况
fig = plt.figure()
fig.set(alpha=0.2)  #设定图表颜色alpha参数

Survived_m = data_train.Survived[data_train.Sex == 'male'].value_counts()
Survived_f = data_train.Survived[data_train.Sex == 'female'].value_counts()
df=pd.DataFrame({u'男性':Survived_m, u'女性':Survived_f})
df.plot(kind='bar', stacked=True)
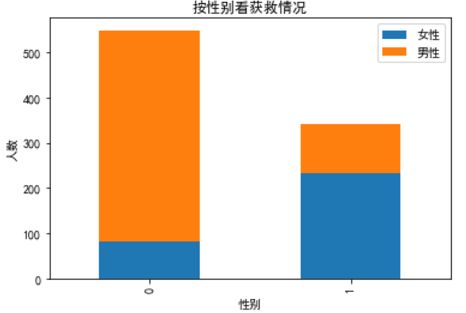
plt.title(u"按性别看获救情况")
plt.xlabel(u"性别") 
plt.ylabel(u"人数")
plt.show()

#然后我们再来看看各种舱级别情况下各性别的获救情况
fig=plt.figure()
fig.set(alpha=0.65) # 设置图像透明度，无所谓
plt.title(u"根据舱等级和性别的获救情况")

ax1=fig.add_subplot(141)
data_train.Survived[data_train.Sex == 'female'][data_train.Pclass != 3].value_counts().plot(kind='bar', label="female highclass", color='#FA2479')
ax1.set_xticklabels([u"获救", u"未获救"], rotation=0)
ax1.legend([u"女性/高级舱"], loc='best')

ax2=fig.add_subplot(142, sharey=ax1)
data_train.Survived[data_train.Sex == 'female'][data_train.Pclass == 3].value_counts().plot(kind='bar', label='female, low class', color='pink')
ax2.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"女性/低级舱"], loc='best')

ax3=fig.add_subplot(143, sharey=ax1)
data_train.Survived[data_train.Sex == 'male'][data_train.Pclass != 3].value_counts().plot(kind='bar', label='male, high class',color='lightblue')
ax3.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"男性/高级舱"], loc='best')

ax4=fig.add_subplot(144, sharey=ax1)
data_train.Survived[data_train.Sex == 'male'][data_train.Pclass == 3].value_counts().plot(kind='bar', label='male low class', color='steelblue')
ax4.set_xticklabels([u"未获救", u"获救"], rotation=0)
plt.legend([u"男性/低级舱"], loc='best')

plt.show()

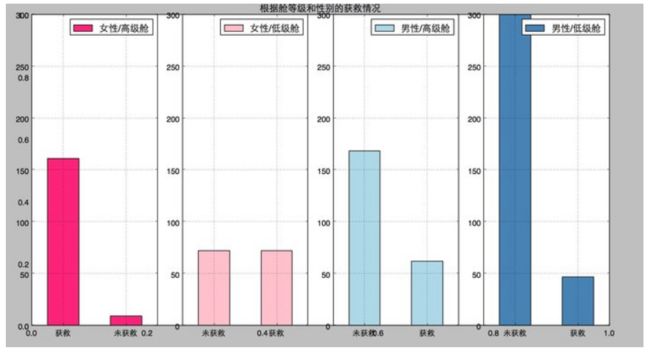
那堂兄弟和父母呢？大家族会有优势么？

g = data_train.groupby(['SibSp','Survived'])
df = pd.DataFrame(g.count()['PassengerId'])
df

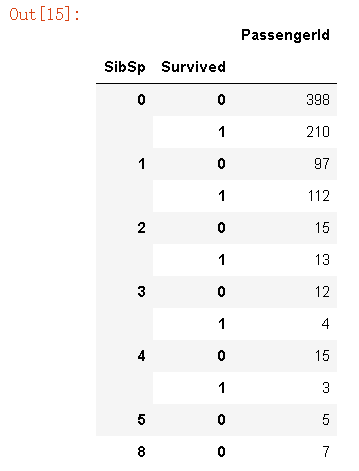
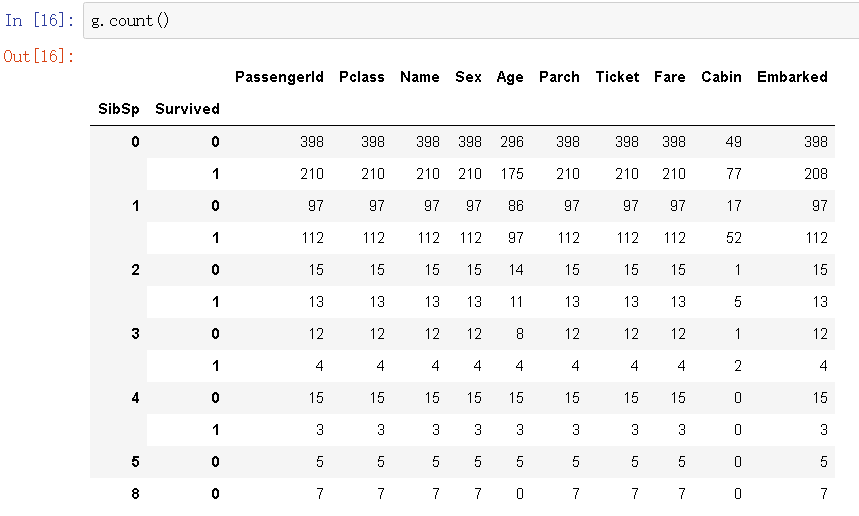
好吧，没看出特别特别明显的规律(为自己的智商感到捉急…)，先作为备选特征，放一放。

看看船票好了

ticket是船票编号，应该是unique的，和最后的结果没有太大的关系，不纳入考虑的特征范畴

cabin只有204个乘客有值，我们先看看它的一个分布

这三三两两的…如此不集中…我们猜一下，也许，前面的ABCDE是指的甲板位置、然后编号是房间号？…

关键是Cabin这鬼属性，应该算作类目型的，本来缺失值就多，还如此不集中，注定是个棘手货…第一感觉，这玩意儿如果直接按照类目特征处理的话，太散了，估计每个因子化后的特征都拿不到什么权重。

加上有那么多缺失值，要不我们先把Cabin缺失与否作为条件(虽然这部分信息缺失可能并非未登记，maybe只是丢失了而已，所以这样做未必妥当)，先在有无Cabin信息这个粗粒度上看看Survived的情况好了。

#cabin的值计数太分散了，绝大多数Cabin值只出现一次。感觉上作为类目，加入特征未必会有效
#那我们一起看看这个值的有无，对于survival的分布状况，影响如何吧
fig = plt.figure()
fig.set(alpha=0.2)  # 设定图表颜色alpha参数

Survived_cabin = data_train.Survived[pd.notnull(data_train.Cabin)].value_counts()
Survived_nocabin = data_train.Survived[pd.isnull(data_train.Cabin)].value_counts()
df=pd.DataFrame({u'有':Survived_cabin, u'无':Survived_nocabin}).transpose()
df.plot(kind='bar', stacked=True)
plt.title(u"按Cabin有无看获救情况")
plt.xlabel(u"Cabin有无") 
plt.ylabel(u"人数")
plt.show()

### 似乎有cabin记录的乘客survival比例稍高，那先试试把这个值分为两类，有cabin值/无cabin值，一会儿加到类别特征好了

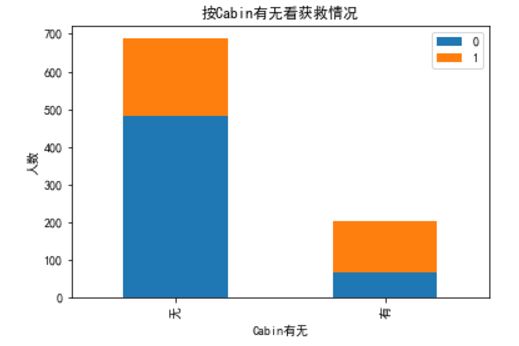
有Cabin记录的似乎获救概率稍高一些，先这么着放一放吧。

先从最突出的数据属性开始吧，对，Cabin和Age，有丢失数据实在是对下一步工作影响太大。

先说Cabin，暂时我们就按照刚才说的，按Cabin有无数据，将这个属性处理成Yes和No两种类型吧。

再说Age：

通常遇到缺值的情况，我们会有几种常见的处理方式

如果缺值的样本占总数比例极高，我们可能就直接舍弃了，作为特征加入的话，可能反倒带入noise，影响最后的结果了

如果缺值的样本适中，而该属性非连续值特征属性(比如说类目属性)，那就把NaN作为一个新类别，加到类别特征中

如果缺值的样本适中，而该属性为连续值特征属性，有时候我们会考虑给定一个step(比如这里的age，我们可以考虑每隔2/3岁为一个步长)，然后把它离散化，之后把NaN作为一个type加到属性类目中。

有些情况下，缺失的值个数并不是特别多，那我们也可以试着根据已有的值，拟合一下数据，补充上。

本例中，后两种处理方式应该都是可行的，我们先试试拟合补全吧(虽然说没有特别多的背景可供我们拟合，这不一定是一个多么好的选择)

我们这里用scikit-learn中的RandomForest来拟合一下缺失的年龄数据

### 使用 RandomForestClassifier 填补缺失的年龄属性
def set_missing_ages(df):
    
    # 把已有的数值型特征取出来丢进Random Forest Regressor中
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]

    # 乘客分成已知年龄和未知年龄两部分
    known_age = age_df[age_df.Age.notnull()].as_matrix()
    unknown_age = age_df[age_df.Age.isnull()].as_matrix()
#     print(unknown_age)
    # y即目标年龄
    y = known_age[:, 0]

    # X即特征属性值
    X = known_age[:, 1:]

    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    rfr.fit(X, y)
    
    # 用得到的模型进行未知年龄结果预测
    predictedAges = rfr.predict(unknown_age[:, 1:])#一个或是2个冒号都一样的
    
    # 用得到的预测结果填补原缺失数据
    df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges
    
    return df, rfr

def set_Cabin_type(df):
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    return df

# data_train, rfr = set_missing_ages(data_train)
# data_train = set_Cabin_type(data_train)
# data_train
# data_train.shape#(891, 12)

因为逻辑回归建模时，需要输入的特征都是数值型特征，我们通常会先对类目型的特征因子化/one-hot编码。

什么叫做因子化/one-hot编码？举个例子：

以Embarked为例，原本一个属性维度，因为其取值可以是[‘S’,’C’,’Q‘]，而将其平展开为’Embarked_C’,’Embarked_S’, ‘Embarked_Q’三个属性

原本Embarked取值为S的，在此处的”Embarked_S”下取值为1，在’Embarked_C’, ‘Embarked_Q’下取值为0

原本Embarked取值为C的，在此处的”Embarked_C”下取值为1，在’Embarked_S’, ‘Embarked_Q’下取值为0

原本Embarked取值为Q的，在此处的”Embarked_Q”下取值为1，在’Embarked_C’, ‘Embarked_S’下取值为0

我们使用pandas的”get_dummies”来完成这个工作，并拼接在原来的”data_train”之上，如下所示。

因为逻辑回归建模时，需要输入的特征都是数值型特征

我们先对类目型的特征离散/因子化

以Cabin为例，原本一个属性维度，因为其取值可以是['yes','no']，而将其平展开为'Cabin_yes','Cabin_no'两个属性

原本Cabin取值为yes的，在此处的'Cabin_yes'下取值为1，在'Cabin_no'下取值为0

原本Cabin取值为no的，在此处的'Cabin_yes'下取值为0，在'Cabin_no'下取值为1

我们使用pandas的get_dummies来完成这个工作，并拼接在原来的data_train之上，如下所示

dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')
df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)#axis为列

import seaborn as sns
#作小提琴图
sns.violinplot(x='Survived',y='Age',data=df)

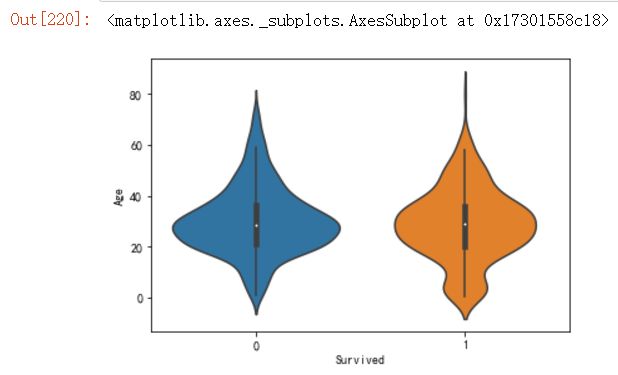
我们还得做一些处理，仔细看看Age和Fare两个属性，乘客的数值幅度变化，也忒大了吧！！如果大### 家了解逻辑回归与梯度下降的话，会知道，各属性值之间scale差距太大，将对收敛速度造成几万点伤### 害值！甚至不收敛！

(╬▔皿▔)…所以我们先用scikit-learn里面的preprocessing模块对这俩货做一个scaling，所谓scaling，### 其实就是将一些变化幅度较大的特征化到[-1,1]之内。

### 接下来我们要接着做一些数据预处理的工作，比如scaling，将一些变化幅度较大的特征化到[-1,1]之内
### 这样可以加速logistic regression的收敛
import sklearn.preprocessing as preprocessing
scaler = preprocessing.StandardScaler()
age_scale_param = scaler.fit(df['Age'])
df['Age_scaled'] = scaler.fit_transform(df['Age'], age_scale_param)#
fare_scale_param = scaler.fit(df['Fare'])
df['Fare_scaled'] = scaler.fit_transform(df['Fare'],fare_scale_param)#
df

我们把需要的feature字段取出来，转成numpy格式，使用scikit-learn中的LogisticRegression建模。

我们把需要的feature字段取出来，转成numpy格式，使用scikit-learn中的LogisticRegression建模

from sklearn import linear_model

train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')#只# #留下满足条件的
train_np = train_df.as_matrix()

# y即Survival结果
y = train_np[:, 0]

# X即特征属性值
X = train_np[:, 1:]

# fit到RandomForestRegressor之中
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
clf.fit(X, y)
    
clf

接下来咱们对训练集和测试集做一样的操作

import sklearn.preprocessing as preprocessing
data_test = pd.read_csv("test.csv")
data_test.loc[(data_test.Fare.isnull()),'Fare'] = 0
# 接着我们对test_data做和train_data中一致的特征变换
# 首先用同样的RandomForestRegressor模型填上丢失的年龄
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].as_matrix()
# 根据特征属性X预测年龄并补上
X_ = null_age[:, 1:]
predictedAges = rfr.predict(X_)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')

df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df_test['Age_scaled'] = preprocessing.scale(df_test['Age'])#, age_scale_param
df_test['Fare_scaled'] = preprocessing.scale(df_test['Fare'])#, fare_scale_param

# df['Fare_scaled'] = preprocessing.scale(df['Fare'])

df_test = df_test.drop(columns='Age')
df_test = df_test.drop(columns='Fare')
df_test = df_test.drop(columns='PassengerId')
df_test.head()

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
# print(test.shape)#(418, 14)
predictions = clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].as_matrix(), 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_predictions.csv", index=False)
test.head()

要判定一下当前模型所处状态(欠拟合or过拟合)

有一个很可能发生的问题是，我们不断地做feature engineering，产生的特征越来越多，用这些特征去训练模型，会对我们的训练集拟合得越来越好，同时也可能在逐步丧失泛化能力，从而在待预测的数据上，表现不佳，也就是发生过拟合问题。

从另一个角度上说，如果模型在待预测的数据上表现不佳，除掉上面说的过拟合问题，也有可能是欠拟合问题，也就是说在训练集上，其实拟合的也不是那么好。

额，这个欠拟合和过拟合怎么解释呢。这么说吧：

过拟合就像是你班那个学数学比较刻板的同学，老师讲过的题目，一字不漏全记下来了，于是老师再出一样的题目，分分钟精确出结果。but数学考试，因为总是碰到新题目，所以成绩不咋地。

欠拟合就像是，咳咳，和博主level差不多的差生。连老师讲的练习题也记不住，于是连老师出一样题目复习的周测都做不好，考试更是可想而知了。

而在机器学习的问题上，对于过拟合和欠拟合两种情形。我们优化的方式是不同的。

对过拟合而言，通常以下策略对结果优化是有用的：

做一下feature selection，挑出较好的feature的subset来做training

提供更多的数据，从而弥补原始数据的bias问题，学习到的model也会更准确

而对于欠拟合而言，我们通常需要更多的feature，更复杂的模型来提高准确度。

著名的learning curve可以帮我们判定我们的模型现在所处的状态。我们以样本数为横坐标，训练和交叉验证集上的错误率作为纵坐标，两种状态分别如下两张图所示：过拟合(overfitting/high variace)，欠拟合(underfitting/high bias)

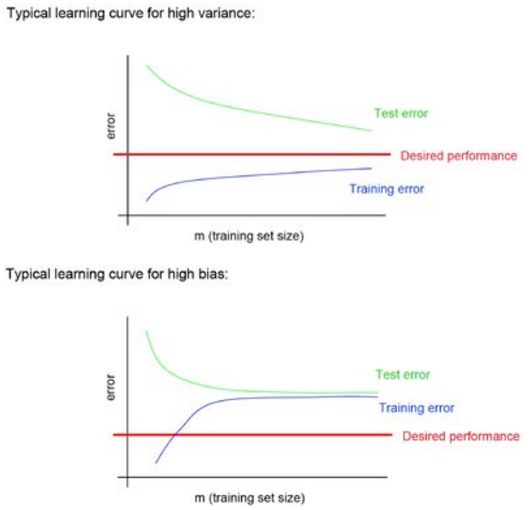
著名的learning curve可以帮我们判定我们的模型现在所处的状态。我们以样本数为横坐标，训练和交叉验证集上的错误率作为纵坐标，两种状态分别如下两张图所示：过拟合(overfitting/high variace)，欠拟合(underfitting/high bias)

我们也可以把错误率替换成准确率(得分)，得到另一种形式的learning curve(sklearn 里面是这么做的)。

回到我们的问题，我们用scikit-learn里面的learning_curve来帮我们分辨我们模型的状态。举个例子，这里我们一起画一下我们最先得到的baseline model的learning curve。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.learning_curve import learning_curve

# 用sklearn的learning_curve得到training_score和cv_score，使用matplotlib画出learning curve
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, 
                        train_sizes=np.linspace(.05, 1., 20), verbose=0, plot=True):
    """
    画出data在某模型上的learning curve.
    参数解释
    ----------
    estimator : 你用的分类器。
    title : 表格的标题。
    X : 输入的feature，numpy类型
    y : 输入的target vector
    ylim : tuple格式的(ymin, ymax), 设定图像中纵坐标的最低点和最高点
    cv : 做cross-validation的时候，数据分成的份数，其中一份作为cv集，其余n-1份作为training(默认为3份)
    n_jobs : 并行的的任务数(默认1)
    """
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes, verbose=verbose)
    
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    if plot:
        plt.figure()
        plt.title(title)
        if ylim is not None:
            plt.ylim(*ylim)
        plt.xlabel(u"训练样本数")
        plt.ylabel(u"得分")
        plt.gca().invert_yaxis()# 翻转坐标轴
        plt.grid()
    
        plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, 
                         alpha=0.1, color="b")
        plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, 
                         alpha=0.1, color="r")
        plt.plot(train_sizes, train_scores_mean, 'o-', color="b", label=u"训练集上得分")
        plt.plot(train_sizes, test_scores_mean, 'o-', color="r", label=u"交叉验证集上得分")
    
        plt.legend(loc="best")
        
        plt.draw()
        plt.gca().invert_yaxis()
        plt.show()
    
    midpoint = ((train_scores_mean[-1] + train_scores_std[-1]) + (test_scores_mean[-1] - test_scores_std[-1])) / 2
    diff = (train_scores_mean[-1] + train_scores_std[-1]) - (test_scores_mean[-1] - test_scores_std[-1])
    return midpoint, diff

plot_learning_curve(clf, u"学习曲线", X, y)

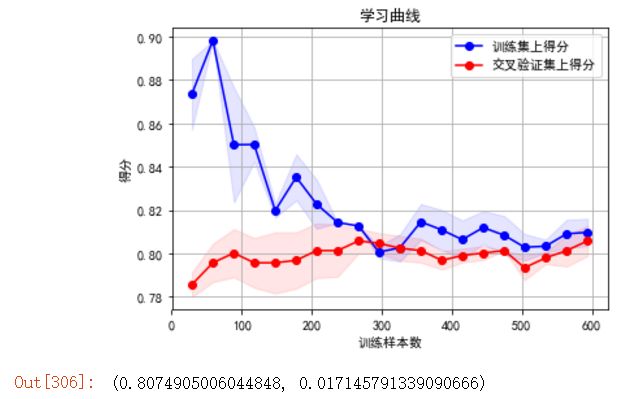
在实际数据上看，我们得到的learning curve没有理论推导的那么光滑哈，但是可以大致看出来，训练集和交叉验证集上的得分曲线走势还是符合预期的。

目前的曲线看来，我们的model并不处于overfitting的状态(overfitting的表现一般是训练集上得分高，而交叉验证集上要低很多，中间的gap比较大)。因此我们可以再做些feature engineering的工作，添加一些新产出的特征或者组合特征到模型中。

接下来，我们就该看看如何优化baseline系统了

我们还有些特征可以再挖掘挖掘

1. 比如说Name和Ticket两个属性被我们完整舍弃了(好吧，其实是一开始我们对于这种，每一条记录都是一个完全不同的值的属性，并没有很直接的处理方式)

2. 比如说，我们想想，年龄的拟合本身也未必是一件非常靠谱的事情

3. 另外，以我们的日常经验，小盆友和老人可能得到的照顾会多一些，这样看的话，年龄作为一个连续值，给一个固定的系数，似乎体现不出两头受照顾的实际情况，所以，说不定我们把年龄离散化，按区段分作类别属性会更合适一些

那怎么样才知道，哪些地方可以优化，哪些优化的方法是promising的呢？

是的

要做交叉验证(cross validation)!

要做交叉验证(cross validation)!

要做交叉验证(cross validation)!

重要的事情说3编！！！

因为test.csv里面并没有Survived这个字段(好吧，这是废话，这明明就是我们要预测的结果)，我们无法在这份数据上评定我们算法在该场景下的效果。。。

我们通常情况下，这么做cross validation：把train.csv分成两部分，一部分用于训练我们需要的模型，另外一部分数据上看我们预测算法的效果。

我们可以用scikit-learn的cross_validation来完成这个工作

我们先看看那些权重绝对值非常大的feature，在我们的模型上：

Sex属性，如果是female会极大提高最后获救的概率，而male会很大程度拉低这个概率。

Pclass属性，1等舱乘客最后获救的概率会上升，而乘客等级为3会极大地拉低这个概率。

有Cabin值会很大程度拉升最后获救概率(这里似乎能看到了一点端倪，事实上从最上面的有无Cabin记录的Survived分布图上看出，即使有Cabin记录的乘客也有一部分遇难了，估计这个属性上我们挖掘还不够)

Age是一个负相关，意味着在我们的模型里，年龄越小，越有获救的优先权(还得回原数据看看这个是否合理）

有一个登船港口S会很大程度拉低获救的概率，另外俩港口压根就没啥作用(这个实际上非常奇怪，因为我们从之前的统计图上并没有看到S港口的获救率非常低，所以也许可以考虑把登船港口这个feature去掉试试)。

船票Fare有小幅度的正相关(并不意味着这个feature作用不大，有可能是我们细化的程度还不够，举个例子，说不定我们得对它离散化，再分至各个乘客等级上？)

噢啦，观察完了，我们现在有一些想法了，但是怎么样才知道，哪些优化的方法是promising的呢？

恩，要靠交叉验证

from sklearn import cross_validation

# 简单看看打分情况
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
all_data = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
X = all_data.as_matrix()[:,1:]
y = all_data.as_matrix()[:,0]
print(cross_validation.cross_val_score(clf, X, y, cv=5))

# 分割数据
split_train, split_cv = cross_validation.train_test_split(df, test_size=0.3, random_state=0)
train_df = split_train.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
# 生成模型
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
clf.fit(train_df.as_matrix()[:,1:], train_df.as_matrix()[:,0])

# 对cross validation数据进行预测
cv_df = split_cv.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions = clf.predict(cv_df.as_matrix()[:,1:])
# split_cv[ predictions != cv_df.as_matrix()[:,0] ].drop()
split_cv[ predictions != cv_df.as_matrix()[:,0] ].shape

[0.57541899 0.70391061 0.64044944 0.66853933 0.65536723]

(87, 18)

# 去除预测错误的case看原始dataframe数据
#split_cv['PredictResult'] = predictions
origin_data_train = pd.read_csv("Train.csv")
origin_data_train.head()
# bad_cases = origin_data_train.loc[origin_data_train['PassengerId'].isin(split_cv[predictions != cv_df.as_matrix()[:,0]]['PassengerId'].values)]
# bad_cases

对比bad case，我们仔细看看我们预测错的样本，到底是哪些特征有问题，咱们处理得还不够细？

我们随便列一些可能可以做的优化操作：

Age属性不使用现在的拟合方式，而是根据名称中的『Mr』『Mrs』『Miss』等的平均值进行填充。

Age不做成一个连续值属性，而是使用一个步长进行离散化，变成离散的类目feature。

Cabin再细化一些，对于有记录的Cabin属性，我们将其分为前面的字母部分(我猜是位置和船层之类的信息) 和 后面的数字部分(应该是房间号，有意思的事情是，如果你仔细看看原始数据，你会发现，这个值大的情况下，似乎获救的可能性高一些)。

Pclass和Sex俩太重要了，我们试着用它们去组出一个组合属性来试试，这也是另外一种程度的细化。

单加一个Child字段，Age<=12的，设为1，其余为0(你去看看数据，确实小盆友优先程度很高啊)

如果名字里面有『Mrs』，而Parch>1的，我们猜测她可能是一个母亲，应该获救的概率也会提高，因此可以多加一个Mother字段，此种情况下设为1，其余情况下设为0

登船港口可以考虑先去掉试试(Q和C本来就没权重，S有点诡异)

把堂兄弟/兄妹 和 Parch 还有自己 个数加在一起组一个Family_size字段(考虑到大家族可能对最后的结果有影响)

Name是一个我们一直没有触碰的属性，我们可以做一些简单的处理，比如说男性中带某些字眼的(‘Capt’, ‘Don’, ‘Major’, ‘Sir’)可以统一到一个Title，女性也一样。

大家接着往下挖掘，可能还可以想到更多可以细挖的部分。我这里先列这些了，然后我们可以使用手头上的”train_df”和”cv_df”开始试验这些feature engineering的tricks是否有效了。

data_train[data_train['Name'].str.contains("Major")]

完整代码

data_train = pd.read_csv("Train.csv")
data_train['Sex_Pclass'] = data_train.Sex + "_" + data_train.Pclass.map(str)

from sklearn.ensemble import RandomForestRegressor
 
### 使用 RandomForestClassifier 填补缺失的年龄属性
def set_missing_ages(df):
    
    # 把已有的数值型特征取出来丢进Random Forest Regressor中
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]

    # 乘客分成已知年龄和未知年龄两部分
    known_age = age_df[age_df.Age.notnull()].as_matrix()
    unknown_age = age_df[age_df.Age.isnull()].as_matrix()

    # y即目标年龄
    y = known_age[:, 0]

    # X即特征属性值
    X = known_age[:, 1:]

    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, n_estimators=200, n_jobs=-1)
    rfr.fit(X, y)
    
    # 用得到的模型进行未知年龄结果预测
    predictedAges = rfr.predict(unknown_age[:, 1::])
    
    # 用得到的预测结果填补原缺失数据
    df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges 
    
    return df, rfr

def set_Cabin_type(df):
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    return df

data_train, rfr = set_missing_ages(data_train)
data_train = set_Cabin_type(data_train)

dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_train['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix= 'Pclass')
dummies_Sex_Pclass = pd.get_dummies(data_train['Sex_Pclass'], prefix= 'Sex_Pclass')


df = pd.concat([data_train, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass, dummies_Sex_Pclass], axis=1)
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked', 'Sex_Pclass'], axis=1, inplace=True)
import sklearn.preprocessing as preprocessing
# scaler = preprocessing.StandardScaler()
# age_scale_param = scaler.fit(df['Age'])
# df['Age_scaled'] = scaler.fit_transform(df['Age'],age_scale_param)
# fare_scale_param = scaler.fit(df['Fare'])
# df['Fare_scaled'] = scaler.fit_transform(df['Fare'], fare_scale_param)
df['Age_scaled'] = preprocessing.scale(df['Age'])
df['Fare_scaled'] = preprocessing.scale(df['Fare'])

from sklearn import linear_model

train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*')
train_np = train_df.as_matrix()

# y即Survival结果
y = train_np[:,0]

# X即特征属性值
X = train_np[:,1:]

# fit到RandomForestRegressor之中
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
clf.fit(X, y)
clf


data_test = pd.read_csv("test.csv")
data_test.loc[ (data_test.Fare.isnull()), 'Fare' ] = 0
data_test['Sex_Pclass'] = data_test.Sex + "_" + data_test.Pclass.map(str)
# 接着我们对test_data做和train_data中一致的特征变换
# 首先用同样的RandomForestRegressor模型填上丢失的年龄
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].as_matrix()
# 根据特征属性X预测年龄并补上
X = null_age[:, 1:]
predictedAges = rfr.predict(X)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')
dummies_Sex_Pclass = pd.get_dummies(data_test['Sex_Pclass'], prefix= 'Sex_Pclass')


df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass, dummies_Sex_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked', 'Sex_Pclass'], axis=1, inplace=True)
# df_test['Age_scaled'] = scaler.fit_transform(df_test['Age'], age_scale_param)#标准化数据
# df_test['Fare_scaled'] = scaler.fit_transform(df_test['Fare'], fare_scale_param)

df_test['Age_scaled'] = preprocessing.scale(df_test['Age'])
df_test['Fare_scaled'] = preprocessing.scale(df_test['Fare'])

df_test.head()

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*')
predictions = clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].as_matrix(), 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_predictions2.csv", index=False)

一般做到后期，咱们要进行模型优化的方法就是模型融合啦

先解释解释啥叫模型融合哈，我们还是举几个例子直观理解一下好了。

大家都看过知识问答的综艺节目中，求助现场观众时候，让观众投票，最高的答案作为自己的答案的形式吧，每个人都有一个判定结果，最后我们相信答案在大多数人手里。

再通俗一点举个例子。你和你班某数学大神关系好，每次作业都『模仿』他的，于是绝大多数情况下，他做对了，你也对了。突然某一天大神脑子犯糊涂，手一抖，写错了一个数，于是…恩，你也只能跟着错了。

我们再来看看另外一个场景，你和你班5个数学大神关系都很好，每次都把他们作业拿过来，对比一下，再『自己做』，那你想想，如果哪天某大神犯糊涂了，写错了，but另外四个写对了啊，那你肯定相信另外4人的是正确答案吧？

最简单的模型融合大概就是这么个意思，比如分类问题，当我们手头上有一堆在同一份数据集上训练得到的分类器(比如logistic regression，SVM，KNN，random forest，神经网络)，那我们让他们都分别去做判定，然后对结果做投票统计，取票#### 数最多的结果为最后结果。

bingo，问题就这么完美的解决了。

模型融合可以比较好地缓解，训练过程中产生的过拟合问题，从而对于结果的准确度提升有一定的帮助。

话说回来，回到我们现在的问题。你看，我们现在只讲了logistic regression，如果我们还想用这个融合思想去提高我们的结果，我们该怎么做呢？

既然这个时候模型没得选，那咱们就在数据上动动手脚咯。大家想想，如果模型出现过拟合现在，一定是在我们的训练上出现拟合过度造成的对吧。

那我们干脆就不要用全部的训练集，每次取训练集的一个subset，做训练，这样，我们虽然用的是同一个机器学习算法，但是得到的模型却是不一样的；同时，因为我们没有任何一份子数据集是全的，因此即使出现过拟合，也是在子训练集上出#### 现过拟合，而不是全体数据上，这样做一个融合，可能对最后的结果有一定的帮助。对，这就是常用的Bagging。

我们用scikit-learn里面的Bagging来完成上面的思路，过程非常简单。代码如下：

from sklearn.ensemble import BaggingRegressor

train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
train_np = train_df.as_matrix()

# y即Survival结果
y = train_np[:, 0]

# X即特征属性值
X = train_np[:, 1:]

# fit到BaggingRegressor之中
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)
bagging_clf = BaggingRegressor(clf, n_estimators=10, max_samples=0.8, max_features=1.0, bootstrap=True, bootstrap_features=False, n_jobs=-1)
bagging_clf.fit(X, y)

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass.*|Mother|Child|Family|Title')
predictions = bagging_clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].as_matrix(), 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_predictions2.csv", index=False)

下面是咱们用别的分类器解决这个问题的代码：

import numpy as np
import pandas as pd
from pandas import  DataFrame
from patsy import dmatrices
import string
from operator import itemgetter
import json
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.grid_search import GridSearchCV
from sklearn.cross_validation import train_test_split,StratifiedShuffleSplit,StratifiedKFold
from sklearn import preprocessing
from sklearn.metrics import classification_report
from sklearn.externals import joblib

##Read configuration parameters

train_file="train.csv"
MODEL_PATH="./"
test_file="test.csv"
SUBMISSION_PATH="./"
seed= 0

print(train_file,seed)

# 输出得分
def report(grid_scores, n_top=3):
    top_scores = sorted(grid_scores, key=itemgetter(1), reverse=True)[:n_top]
    for i, score in enumerate(top_scores):
        print("Model with rank: {0}".format(i + 1))
        print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
              score.mean_validation_score,
              np.std(score.cv_validation_scores)))
        print("Parameters: {0}".format(score.parameters))
        print("")

#清理和处理数据
def substrings_in_string(big_string, substrings):
    for substring in substrings:
        if big_string.find(substring) != -1:
            return substring
    print (big_string)
    return np.nan

le = preprocessing.LabelEncoder()
enc=preprocessing.OneHotEncoder()

def clean_and_munge_data(df):
    #处理缺省值
    df.Fare = df.Fare.map(lambda x: np.nan if x==0 else x)
    #处理一下名字，生成Title字段
    title_list=['Mrs', 'Mr', 'Master', 'Miss', 'Major', 'Rev',
                'Dr', 'Ms', 'Mlle','Col', 'Capt', 'Mme', 'Countess',
                'Don', 'Jonkheer']
    df['Title']=df['Name'].map(lambda x: substrings_in_string(x, title_list))

    #处理特殊的称呼，全处理成mr, mrs, miss, master
    def replace_titles(x):
        title=x['Title']
        if title in ['Mr','Don', 'Major', 'Capt', 'Jonkheer', 'Rev', 'Col']:
            return 'Mr'
        elif title in ['Master']:
            return 'Master'
        elif title in ['Countess', 'Mme','Mrs']:
            return 'Mrs'
        elif title in ['Mlle', 'Ms','Miss']:
            return 'Miss'
        elif title =='Dr':
            if x['Sex']=='Male':
                return 'Mr'
            else:
                return 'Mrs'
        elif title =='':
            if x['Sex']=='Male':
                return 'Master'
            else:
                return 'Miss'
        else:
            return title

    df['Title']=df.apply(replace_titles, axis=1)

    #看看家族是否够大，咳咳
    df['Family_Size']=df['SibSp']+df['Parch']
    df['Family']=df['SibSp']*df['Parch']


    df.loc[ (df.Fare.isnull())&(df.Pclass==1),'Fare'] =np.median(df[df['Pclass'] == 1]['Fare'].dropna())
    df.loc[ (df.Fare.isnull())&(df.Pclass==2),'Fare'] =np.median( df[df['Pclass'] == 2]['Fare'].dropna())
    df.loc[ (df.Fare.isnull())&(df.Pclass==3),'Fare'] = np.median(df[df['Pclass'] == 3]['Fare'].dropna())

    df['Gender'] = df['Sex'].map( {'female': 0, 'male': 1} ).astype(int)

    df['AgeFill']=df['Age']
    mean_ages = np.zeros(4)
    mean_ages[0]=np.average(df[df['Title'] == 'Miss']['Age'].dropna())
    mean_ages[1]=np.average(df[df['Title'] == 'Mrs']['Age'].dropna())
    mean_ages[2]=np.average(df[df['Title'] == 'Mr']['Age'].dropna())
    mean_ages[3]=np.average(df[df['Title'] == 'Master']['Age'].dropna())
    df.loc[ (df.Age.isnull()) & (df.Title == 'Miss') ,'AgeFill'] = mean_ages[0]
    df.loc[ (df.Age.isnull()) & (df.Title == 'Mrs') ,'AgeFill'] = mean_ages[1]
    df.loc[ (df.Age.isnull()) & (df.Title == 'Mr') ,'AgeFill'] = mean_ages[2]
    df.loc[ (df.Age.isnull()) & (df.Title == 'Master') ,'AgeFill'] = mean_ages[3]

    df['AgeCat']=df['AgeFill']
    df.loc[ (df.AgeFill<=10) ,'AgeCat'] = 'child'
    df.loc[ (df.AgeFill>60),'AgeCat'] = 'aged'
    df.loc[ (df.AgeFill>10) & (df.AgeFill <=30) ,'AgeCat'] = 'adult'
    df.loc[ (df.AgeFill>30) & (df.AgeFill <=60) ,'AgeCat'] = 'senior'

    df.Embarked = df.Embarked.fillna('S')


    df.loc[ df.Cabin.isnull()==True,'Cabin'] = 0.5
    df.loc[ df.Cabin.isnull()==False,'Cabin'] = 1.5

    df['Fare_Per_Person']=df['Fare']/(df['Family_Size']+1)

    #Age times class

    df['AgeClass']=df['AgeFill']*df['Pclass']
    df['ClassFare']=df['Pclass']*df['Fare_Per_Person']


    df['HighLow']=df['Pclass']
    df.loc[ (df.Fare_Per_Person<8) ,'HighLow'] = 'Low'
    df.loc[ (df.Fare_Per_Person>=8) ,'HighLow'] = 'High'



    le.fit(df['Sex'] )
    x_sex=le.transform(df['Sex'])
    df['Sex']=x_sex.astype(np.float)

    le.fit( df['Ticket'])
    x_Ticket=le.transform( df['Ticket'])
    df['Ticket']=x_Ticket.astype(np.float)

    le.fit(df['Title'])
    x_title=le.transform(df['Title'])
    df['Title'] =x_title.astype(np.float)

    le.fit(df['HighLow'])
    x_hl=le.transform(df['HighLow'])
    df['HighLow']=x_hl.astype(np.float)


    le.fit(df['AgeCat'])
    x_age=le.transform(df['AgeCat'])
    df['AgeCat'] =x_age.astype(np.float)

    le.fit(df['Embarked'])
    x_emb=le.transform(df['Embarked'])
    df['Embarked']=x_emb.astype(np.float)

    df = df.drop(['PassengerId','Name','Age','Cabin'], axis=1) #remove Name,Age and PassengerId


    return df

#读取数据
traindf=pd.read_csv(train_file)
##清洗数据
df=clean_and_munge_data(traindf)
########################################formula################################
 
formula_ml='Survived~Pclass+C(Title)+Sex+C(AgeCat)+Fare_Per_Person+Fare+Family_Size' 

y_train, x_train = dmatrices(formula_ml, data=df, return_type='dataframe')
y_train = np.asarray(y_train).ravel()
print(y_train.shape,x_train.shape)

##选择训练和测试集
X_train, X_test, Y_train, Y_test = train_test_split(x_train, y_train, test_size=0.2,random_state=seed)
#初始化分类器
clf=RandomForestClassifier(n_estimators=500, criterion='entropy', max_depth=5, min_samples_split=1,
  min_samples_leaf=1, max_features='auto',    bootstrap=False, oob_score=False, n_jobs=1, random_state=seed,
  verbose=0)

###grid search找到最好的参数
param_grid = dict( )
##创建分类pipeline
pipeline=Pipeline([ ('clf',clf) ])
cv = StratifiedShuffleSplit(Y_train, n_iter=10, test_size=0.2, train_size=None, indices=None,random_state=seed, n_iterations=None)
grid_search = GridSearchCV(pipeline, param_grid=param_grid, verbose=3,scoring='accuracy',cv=cv).fit(X_train, Y_train)
# 对结果打分
print("Best score: %0.3f" % grid_search.best_score_)
print(grid_search.best_estimator_)
report(grid_search.grid_scores_)
 
print('-----grid search end------------')
print ('on all train set')
scores = cross_val_score(grid_search.best_estimator_, x_train, y_train,cv=3,scoring='accuracy')
print (scores.mean(),scores)
print ('on test set')
scores = cross_val_score(grid_search.best_estimator_, X_test, Y_test,cv=3,scoring='accuracy')
print (scores.mean(),scores)

# 对结果打分

print(classification_report(Y_train, grid_search.best_estimator_.predict(X_train) ))
print('test data')
print(classification_report(Y_test, grid_search.best_estimator_.predict(X_test) ))

model_file=MODEL_PATH+'model-rf.pkl'
joblib.dump(grid_search.best_estimator_, model_file)

转载于:https://www.cnblogs.com/nxf-rabbit75/p/9680878.html