Leetcode题解-算法-贪心算法
文章目录
- 1、数对可以组成的最长链
- 2、分配饼干
- 3、不重叠的区间个数
- 4、最少需要多少飞镖刺破气球
- 5、根据身高序号重排序
- 6、买卖股票最大的收益
- 7、买卖股票最大的收益Ⅱ
- 8、种植花朵
- 9、判断是否是字串
- 10、修改一个数成为非递减数组
- 11、连续子数组的最大和
- 12、分隔字符串使同种字符出现在一起
1、数对可以组成的最长链
646. Maximum Length of Pair Chain(Medium)
You are given n pairs of numbers. In every pair, the first number is always smaller than the second number.
Now, we define a pair (c, d) can follow another pair (a, b) if and only if b < c. Chain of pairs can be formed in this fashion.
Given a set of pairs, find the length longest chain which can be formed. You needn’t use up all the given pairs. You can select pairs in any order.
Example 1:
Input: [[1,2], [2,3], [3,4]]
Output: 2
Explanation: The longest chain is [1,2] -> [3,4]
Note:
The number of given pairs will be in the range [1, 1000].
问题分析:
方法一:贪心
对所有的数对按照第二个数的大小进行排序。第一步选结束数字最小的那个数对。 然后,每步都选和上一个选中的数对不冲突且结束数字最小的那个数。
class Solution {
public:
int findLongestChain(vector<vector<int>>& pairs) {
//按数对中第二个数的大小进行排序
sort(pairs.begin(), pairs.end(), [](const vector<int>& a, const vector<int>& b){ return a[1] < b[1]; });
int len=pairs.size();
int count=1;
int end=pairs[0][1];
for(int i=1;i<len;i++)
{
if(pairs[i][0]>end)
{
end=pairs[i][1];
count++;
}
}
return count;
}
};
方法二:动态规划
对所有的数对按照第一个数的大小进行排序。子问题为数对 pairs[i](i=1, 2, 3…N)为终点的最长链。a[i] 表示已数对 pairs[i]为终点的链长度。
- 初始状态:a[i] = 1
- a[i] = max { a[i], a[j]+1} 0<= j< i 且 pairs[i][0]>pairs[j][1]
再寻找 a[i] 的最大值。
class Solution {
public:
int findLongestChain(vector<vector<int>>& pairs) {
sort(pairs.begin(),pairs.end(),[](vector<int>a,vector<int>b){return a[0]<b[0];});
int len=pairs.size();
vector<int>a(len,1);
for(int i=1;i<len;i++)
{
for(int j=0;j<i;j++)
if(pairs[i][0]>pairs[j][1])
a[i]=max(a[i],a[j]+1);
}
int ans=0;
for(int i=0;i<len;i++)
if(a[i]>ans)
ans=a[i];
return ans;
}
};
2、分配饼干
455. Assign Cookies(Easy)
Assume you are an awesome parent and want to give your children some cookies. But, you should give each child at most one cookie. Each child i has a greed factor gi, which is the minimum size of a cookie that the child will be content with; and each cookie j has a size sj. If sj >= gi, we can assign the cookie j to the child i, and the child i will be content. Your goal is to maximize the number of your content children and output the maximum number.
Note:
You may assume the greed factor is always positive.
You cannot assign more than one cookie to one child.
Example 1:
Input: [1,2,3], [1,1]
Output: 1
Explanation: You have 3 children and 2 cookies. The greed factors of 3 children are 1, 2, 3.
And even though you have 2 cookies, since their size is both 1, you could only make the child whose greed factor is 1 content.
You need to output 1.
Example 2:
Input: [1,2], [1,2,3]
Output: 2
Explanation: You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.
问题分析:
有一些饼干,一些孩子,每个孩子都有一个满足度,每个饼干都有一个大小,饼干大小大于等于孩子满足度时,孩子才会获得满足,每个孩子分配一个饼干。问最多有多少孩子满足。
为了不浪费饼干,应该给每个孩子分配可以使该孩子满足,且大小最小的饼干。
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(),g.end());
sort(s.begin(),s.end());
int i=0,j=0;
int count=0;
while(i<g.size()&&j<s.size())
{
if(g[i]<=s[j])
{
i++;
count++;
}
j++;
}
return count;
}
};
3、不重叠的区间个数
435. Non-overlapping Intervals(Medium)
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note:
- You may assume the interval’s end point is always bigger than its start point.
- Intervals like [1,2] and [2,3] have borders “touching” but they don’t overlap each other.
Example 1:
Input: [ [1,2], [2,3], [3,4], [1,3] ]
Output: 1
Explanation: [1,3] can be removed and the rest of intervals are non-overlapping.
Example 2:
Input: [ [1,2], [1,2], [1,2] ]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.
Example 3:
Input: [ [1,2], [2,3] ]
Output: 0
Explanation: You don’t need to remove any of the intervals since they’re already non-overlapping.
为了让区间不重复,最少需要移除多少个区间。
贪心思想,计算不重复的区间最多多少个,然后用区间总个数减去不重叠区间的个数。将区间排序按照结尾数字排序,这次选的结尾越小,留给后面的区间的空间越大。每次选结尾最小且与前面不重叠的那个区间。
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
int n=intervals.size();
if(n==0)
return 0;
sort(intervals.begin(),intervals.end(),[](vector<int>a,vector<int>b){return a[1]<b[1];});
int end=intervals[0][1];
int count=1;
for(auto c:intervals)
{
if(c[0]>=end)
{
end=c[1];
count++;
}
}
return n-count;
}
};
4、最少需要多少飞镖刺破气球
452. Minimum Number of Arrows to Burst Balloons(Medium)
问题描述:
气球在水平轴上摆放,可以重叠,每个气球有起始位置和结束位置,飞镖垂直射向坐标轴,最少需要多少个飞镖。
这里是计算不重叠的区间个数一共有多少个,按照每个区间的结束坐标排序,选取第一个区间,以后每次选取与当前区间不重叠且结束坐标最小的区间。
pair
Example:
Input:
[[10,16], [2,8], [1,6], [7,12]]
Output:
2
Explanation:
One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).
class Solution {
public:
int findMinArrowShots(vector<pair<int, int>>& points) {
if(points.size()==0)
return 0;
sort(points.begin(),points.end(),[](pair<int,int>a,pair<int,int>b){return a.second<b.second;});
int count=1;
int end=points[0].second;
for(auto c:points)
{
if(c.first>end)
{
count++;
end=c.second;
}
}
return count;
}
};
5、根据身高序号重排序
406. Queue Reconstruction by Height(Medium)
问题描述:每个人用两个数(h,k)描述,h 表示身高,k 表示排在前面的比自己高或者等高的人一共有 k 个,现在需要将每个人放到对应的位置上。
Example:
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
问题分析:
按照身高降序排序,身高相等的按序号升序排序,遍历所有的人,将每个人插到对应位置上。
举例说明:[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
排序:
[7, 0] [7, 1] [6, 1] [5, 0] [5, 2] [4, 4]
插入:
[7, 0]
[7, 0] [7, 1]
[7, 0] [6, 1] [7, 1]
[5, 0] [7, 0] [6, 1] [7, 1]
[5, 0] [7, 0] 5, 2] [6, 1] [7, 1]
[5, 0] [7, 0] 5, 2] [6, 1] [4, 4] [7, 1]
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
auto cmp = [](const vector<int> &a, const vector<int> &b) {
return a[0] > b[0] || (a[0] == b[0] && a[1] < b[1]);
};
sort(people.begin(), people.end(), cmp);
vector<vector<int>>res;
for(auto c:people)
res.insert(res.begin()+c[1],c);//必须插入到有效的迭代器范围中,包括尾迭代器
return res;
}
};
6、买卖股票最大的收益
121. Best Time to Buy and Sell Stock(Easy)
Say you have an array for which the ith element is the price of a given stock on day i.If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example 1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
记录前面的最小价格,将这个价格作为买入价格,当前价格作为卖出价格,当前利润大于前面的利润,更新利润。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res=0;
int len=prices.size();
if(len==0) return res;
int sma=prices[0];
for(int i=1;i<len;i++){
if(prices[i]<sma)
sma=prices[i];
res=max(res,prices[i]-sma);
}
return res;
}
};
7、买卖股票最大的收益Ⅱ
122. Best Time to Buy and Sell Stock II(Easy)
Say you have an array for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).
Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Example 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
Example 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
股票每天有一个价格,不限制买卖的次数,股票卖出后才能再买,问可以得到饿最大利润是多少。
问题分析:
只要价格在增加,就有收益。
对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,因此当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res=0;
for(int i=1;i<prices.size();i++)
if(prices[i]>prices[i-1])
res+=prices[i]-prices[i-1];
return res;
}
};
8、种植花朵
605. Can Place Flowers(Easy)
Suppose you have a long flowerbed in which some of the plots are planted and some are not. However, flowers cannot be planted in adjacent plots - they would compete for water and both would die.
Given a flowerbed (represented as an array containing 0 and 1, where 0 means empty and 1 means not empty), and a number n, return if n new flowers can be planted in it without violating the no-adjacent-flowers rule.
Example 1:
Input: flowerbed = [1,0,0,0,1], n = 1
Output: True
Example 2:
Input: flowerbed = [1,0,0,0,1], n = 2
Output: False
Note:
The input array won’t violate no-adjacent-flowers rule.
The input array size is in the range of [1, 20000].
n is a non-negative integer which won’t exceed the input array size.
一个数组中只有 0 和 1,要求 1 的左右两侧不能为 0,想在现在的数组中将一部分 0 换成 1,问能不能放下给定数量的 1。
问题分析:
该位置上的 0 可以被换成 1 要满足如下条件:该位置为 0,并且该位置左侧为 0 或者在最左端,并且该位置右侧为 0,或者在最右端。
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
int i=0,count=0;
int len=flowerbed.size();
while(i<len){
if(flowerbed[i]==0 && (i==0||flowerbed[i-1]==0) && (i==len-1||flowerbed[i+1]==0)){
count++;
flowerbed[i]=1;
}
i++;
}
return n<=count;
}
};
9、判断是否是字串
392. Is Subsequence(Medium)
Given a string s and a string t, check if s is subsequence of t.You may assume that there is only lower case English letters in both s and t. t is potentially a very long (length ~= 500,000) string, and s is a short string (<=100).
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ace” is a subsequence of “abcde” while “aec” is not).
Example 1:
s = “abc”, t = “ahbgdc”
Return true.
Example 2:
s = “axc”, t = “ahbgdc”
Return false.
问题分析:
从前向后匹配字符,若匹配成功,字串下标加1,继续匹配。
class Solution {
public:
bool isSubsequence(string s, string t) {
int i=0,j=0;
while(i<s.size()&&j<t.size()){
if(s[i]==t[j])
i++;
j++;
}
if(i==s.size())
return true;
return false;
}
};
10、修改一个数成为非递减数组
665. Non-decreasing Array(Easy)
Given an array with n integers, your task is to check if it could become non-decreasing by modifying at most 1 element.
Example 1:
Input: [4,2,3]
Output: True
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.
Example 2:
Input: [4,2,1]
Output: False
Explanation: You can’t get a non-decreasing array by modify at most one element.
方法一:修改数组
在出现 nums[i] < nums[i - 1] 时,需要考虑的是应该修改数组的哪个数,为了不影响后续的操作,应优先将较大的数改小,即优先考虑 nums[i - 1] = nums[i],如果令 nums[i] = nums[i - 1],就使得 nums[i] 变大,不利于后续操作。还要考虑数组要非递减,如果 nums[i] < nums[i - 2],修改 nums[i - 1] = nums[i] 不能使数组成为非递减数组,这时只能修改 nums[i] = nums[i - 1]。
class Solution {
public:
bool checkPossibility(vector<int>& nums) {
int cnt = 0;
int n = nums.size();
for (int i = 1; i < n; i++){
if (nums[i - 1] > nums[i]){
cnt++;
if (i >= 2 && nums[i] < nums[i - 2])
nums[i] = nums[i - 1];
else
nums[i - 1] = nums[i];
}
}
return cnt < 2;
}
};
方法二:理论分析
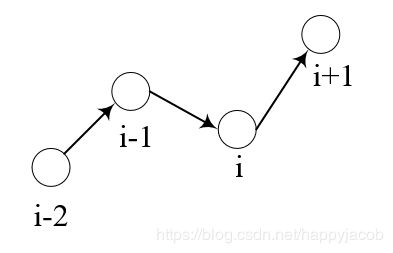
当出现 nums[i] < nums[i - 1] 时,有两种方案可以选择来修改数组,第一种,将 i - 1 节点变小,第二种,将 i 节点变大。
如果 i >= 2 && nums[i] >= nums[i - 2] 表示可以将 i - 1 节点变小,更改次数加 1
如果 i <= n - 2 && nums[i + 1] >= nums[i - 1] 表示可以将 i 节点变大,更改次数加 1
如果 i 为 1 或 n - 1,一定可以修改
上面条件不满足,一定不能修改为非递减数组。
最后判断修改次数。
class Solution {
public:
bool checkPossibility(vector<int>& nums) {
int cnt = 0;
int n = nums.size();
for (int i = 1; i < n; i++){
if (nums[i - 1] > nums[i]){
if (i == 1 || i == n-1)
cnt++;
else if ((i >= 2 && nums[i] >= nums[i-2]) || (i <= n-2 && nums[i+1] >= nums[i-1]))
cnt++;
else
return false;
}
}
if(cnt > 1) return false;
return true;
}
};
11、连续子数组的最大和
53. Maximum Subarray(Easy)
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int sum = 0;
int maxsum = nums[0];
for (int i = 0; i < nums.size(); i++){
sum += nums[i];
maxsum = max(sum, maxsum);
if(sum < 0) sum = 0;
}
return maxsum;
}
};
12、分隔字符串使同种字符出现在一起
763. Partition Labels(Medium)
Example:
Input: S = “ababcbacadefegdehijhklij”
Output: [9,7,8]
Explanation:
The partition is “ababcbaca”, “defegde”, “hijhklij”.
This is a partition so that each letter appears in at most one part.
A partition like “ababcbacadefegde”, “hijhklij” is incorrect, because it splits S into less parts.
解题思路:贪心算法
首先统计字符串中每种字符最后一次出现的位置。从前向后遍历字符串种每一个字符,查看这些字符最后一次出现的位置,当前位置等于前面这些字符最后一次出现的位置时,说明前面查看的这些字符在后面的字符中不会出现,可以在这里将字符串分隔开。
class Solution {
public:
vector<int> partitionLabels(string S) {
vector<int>last(26, 0);
vector<int>res;
for (int i = 0; i < S.size(); i++) //统计每种字符最后一次出现的位置
last[S[i] - 'a'] = i;
int j = 0, pre = 0;
for (int i = 0; i < S.size(); i++){
j = max(j, last[S[i] - 'a']); //前面这些字符最后一次出现的位置
if(i == j){ //当前位置等于前面的所有字符最后一次出现的位置,分隔
res.push_back(j - pre + 1);
pre = i + 1;
}
}
return res;
}
};
时间复杂度:O(n)
空间复杂度:O(1)