7.8 最优二叉树与哈夫曼编码

最优二叉树定义

对于一棵树，可以将每一个结点赋一个数值，称之为结点的权重(weight)，简称权。定义一棵树上某个结点 Vi 的带权路径长度(weighted path length)为从根节点到该结点的路径长度 li 与该结点上权重 wi 的乘积。一棵树的带权路径长度是指所有结点的带权路径长度之和，即 L=∑n0i=1wili ，其中 n0 是叶子结点的个数（度为零的顶点）。
对于由 n0 个叶子结点构成的二叉树来说，取带权路径长度 L 最小的称为最优二叉树，也叫哈夫曼树(Huffman Tree)。

哈夫曼编码

哈夫曼编码是一种常见的压缩算法，通常可以节省20%~90%的空间，具体取决于数据的特性。
假设原数据使用ASCII码表示，它本身是一种二进制码，但是ASCII码规定一个字符用8个二进制位表示（7位有效加上1位校验），浪费大量的存储空间。也可以做一个简单映射，比如现在需要表示62个字符（大小写A~Z，0~9）构成的一串文字，那么可以令A用0表示，B用1，C用10表示，…。这样为了能够表示所有的字符，需要 ⌈log262⌉=6 个二进制位，空间开销依然很大。
上面的编码方法为定长编码，而哈夫曼编码是一种变长编码(variable-length code)。
对于任意一个字符，可以把它的二进制表示看作一棵二叉树中某个叶子结点。也就是说，从根结点开始，碰到0则走向左孩子，碰到1则走向右孩子。这样走到叶子结点能够唯一确定这个字符而不至于引发歧义。也就是说，哈夫曼编码需要保证所有字符编码后互不有公共前缀，二叉树恰能保证这一点。
由此可见，对于某个叶子结点 Vi 上的字符，其路径长度就是该叶子的深度 li 。考虑到该结点的权 wi 就是该结点上的字符出现的频率，因此该结点的带权路径长度为 wili 。
因此，哈夫曼编码问题本质上就是构造一棵最优二叉树的过程。

最优二叉树的构造算法

最优二叉树的构造算法本质上是一个贪心算法，这里不给出最优二叉树满足贪心算法最优子结构的证明，只是简要叙述构造哈夫曼树的具体算法。
（1）已知字符集 Σ 和 Σ 中每个字符出现的频度。构造 |Σ| 个结点构成的集合 Q ，结点分别包含字符和该字符出现的频度。
（2）每次从 Q 中取出两个频度最小的结点 x 和 y ，将其分别作为左右子树构造出一棵新的二叉树，其根结点为 z ，并将 z 放进 Q 中。
（3）如此循环，直到 |Q|=1 。
按照上述算法构造出的最优二叉树，非叶子结点度均为 2 （因为每次取两个，只可能构造出度为2的子树），度为 0 的结点只可能是叶子结点。因此 n1=0 。又 E=V−1 ， E=n1+2n2 ， V=n0+n1+n2 ，则可得 n0 个叶子结点构成的最优二叉树，共有 2n0−1 个结点。

下面是使用C++的一个实现。基本上说明都在注释里，唯一需要说的就是比较两个指针直接重载operator<是不行的（因为指针都是系统类型），必须要使用仿函数（对struct重载operator()）。这样就可以使用STL的优先队列了。还有就是位操作，我是参考http://blog.csdn.net/morewindows/article/details/7354571 这篇文章的，讲的很详细。

template<int _DictSize>
class HuffmanCode
{
private:
    struct HuffmanTreeNode
    {
        HuffmanTreeNode * _left;
        HuffmanTreeNode * _right;
        unsigned char _val;    //unsigned char表示二进制字节（8bit）
        int _freq;    //权重域
        HuffmanTreeNode(char val, int freq) :_val(val), _freq(freq){
            _left = _right = nullptr;
        }
    };
    /**
    * 哈夫曼树结点比较器。
    */
    struct HuffmanTreeNodeComparer
    {
        /**
        * 比较函数，用来比较两个哈夫曼树结点的权。
        * @param HuffmanTreeNode * n1 需要比较的哈夫曼树结点1
        * @param HuffmanTreeNode * n2 需要比较的哈夫曼树结点2
        * @return 若n1的权比n2大，返回true，反之false.
        */
        bool operator()(HuffmanTreeNode * n1, HuffmanTreeNode * n2){
            return n1->_freq > n2->_freq;
        }
    };

    HuffmanTreeNode * _root;    //哈夫曼树的根节点。
    vector<int> _dict[_DictSize];    //保存字典。
    /**
    * 构造字典的递归辅助函数。
    * @param HuffmanTreeNode * node 当前遍历的结点指针。
    * @param vector & trace 表示从根节点到当前结点的路径。
    */
    void build_dict(HuffmanTreeNode * node, vector<int> & trace){
        if (!node->_left && !node->_right){
            //下面是利用了std::vector “=”重载的复制功能。
            _dict[node->_val] = trace;
            return;
        }
        if (node->_left){
            trace.push_back(0);
            build_dict(node->_left, trace);
            trace.pop_back();    //因为是引用类型，递归后需要恢复状态，即最后将末尾元素弹出。下同。
        }
        if (node->_right){
            trace.push_back(1);
            build_dict(node->_right, trace);
            trace.pop_back();
        }
    }
    void build_dict(){
        vector<int> trace;
        build_dict(_root, trace);
    }
public:
    /**
    * 一个Buffer结构体，用来存放缓冲。
    */
    struct Buffer
    {
        size_t length;    //缓冲内容的真实长度（字节）
        size_t capacity;  //缓冲区容量
        unsigned char * data;  //缓冲区的内容
        /**
        * 构造函数.
        * @param size_t init_size 设置容量大小。
        */
        Buffer(size_t init_size){
            capacity = init_size;
            data = new unsigned char[init_size];
            for (size_t i = 0; i < init_size; i++)
                data[i] = 0;
            length = 0;
        }
        /**
        * 析构函数
        */
        ~Buffer(){
            delete[] data;
        }
    };
    /**
    * 构造函数，用来创建哈夫曼树。
    * @param std::map inputs 字母表以及出现的频度
    */
    HuffmanCode(std::map<char, int> inputs){
        std::priority_queuevector, HuffmanTreeNodeComparer> pq;  //使用优先队列来完成每次提取两个最小权重结点的操作。
        //先将字典中的所有的单词都添加到森林（优先队列表示）。
        for (auto it = inputs.begin(); it != inputs.end(); ++it)
            pq.push(new HuffmanTreeNode(it->first, it->second));
        //因为要输出最后的根节点，因此循环边界条件并不是优先队列为空。
        while (pq.size() != 1){
            HuffmanTreeNode * x = pq.top();
            pq.pop();
            HuffmanTreeNode * y = pq.top();
            pq.pop();
            HuffmanTreeNode * z = new HuffmanTreeNode(0, x->_freq + y->_freq);
            z->_left = x;
            z->_right = y;
            pq.push(z);
        }
        _root = pq.top();
        pq.pop();
        //建立字典。
        build_dict();
    }
    /**
    * 进行哈夫曼编码。
    * @param Buffer * src 需要编码的二进制数据
    * @param Buffer * dest 存放编码后的二进制数据的缓冲区
    * @return Buffer * 返回编码后的二进制缓冲区
    */
    Buffer * encode(Buffer * src, Buffer * dest){
        size_t i;
        size_t encoded_sz = 0;    //最终编码后的二进制串长度
        for (i = 0; i < src->length; i++){
            //取已经编好的码。
            unsigned char srcbyte = src->data[i];
            vector<int> * code = _dict + srcbyte;
            //这个循环处理每个字符。
            for (int j = 0; j < code->size(); j++){
                //如果往1的方向走，就将该位设置为1。
                if (code->at(j))
                    dest->data[(encoded_sz + j) / 8] |= (1 << ((encoded_sz + j) % 8));
            }
            encoded_sz += code->size();
        }
        dest->length = encoded_sz / 8 + 1;    //处理实际字节长度
        return dest;
    }
    /**
    * 对以有的编码进行解码。
    * @param Buffer * src 需要解码的二进制数据
    * @param Buffer * dest 存放解码后的二进制数据的缓冲区
    * @return Buffer * 返回解码后的二进制缓冲区
    */
    Buffer * decode(Buffer * src, Buffer * dest){
        size_t i, j = 0;
        HuffmanTreeNode * hnode = _root;
        //逐位读取数据，然后在哈夫曼树中进行查找。因此需要乘8。
        for (i = 0; i < src->length * 8; i++){
            if ((src->data[i / 8] >> (i % 8)) & 1)
                hnode = hnode->_right;
            else
                hnode = hnode->_left;
            //不是叶子结点，不包含编码，需要继续寻找
            if (hnode->_left || hnode->_right)
                continue;
            //找到叶子结点，将叶子结点的编码（1字节）写入缓冲区
            dest->data[j++] = hnode->_val;
            //找到了值以后，重置为根节点，为下一次寻找做准备。
            hnode = _root;
        }
        dest->length = j;//设置解码后数据的实际长度
        return dest;
    }
};

一个简单的压缩程序

利用上面的HuffmanCode类，可以简单实现一个压缩程序。把需要压缩的二进制数据看作只包含字符集合 Σ={0,1} 的字符串。将文件中的每一个字节看作一个字符，统计每个字符出现的频率，就可以利用哈夫曼编码进行压缩了。
下面给出主程序。需要说明的地方不多，之一就是fread的返回值问题。关于fread的四个参数，fread(buf,item,count,fp) 表示，每次读item大小的数据块，分count次来读。返回读取成功的次数。另外就是filelength(fileno(fp))的方法获取文件大小。

int main(){


#define BLK_SZ 65536        //64KB 块空间（每次处理64KB）
#define EXT_BLK_SZ 16384    //16KB 额外块空间（防止溢出）
#define DICT_SZ 256         //字典大小

#define INPUT "F:/sq_ratotal1.sql"
#define OUTPUT "F:/sq_ratotal1.archive"

    FILE * fp_read = fopen(INPUT, "rb");
    long input_size = filelength(fileno(fp_read));
    FILE * fp_write = fopen(OUTPUT, "wb");
    HuffmanCode::Buffer * src = new HuffmanCode::Buffer(BLK_SZ + EXT_BLK_SZ);
    int blkid = 0;
    std::map<char, int> inputs;
    clock_t start, end;
    clock_t tstart = clock();
    while (!feof(fp_read))
    {
        start = clock();
        inputs.clear();
        int fresult = fread(src->data, BLK_SZ, 1, fp_read);
        src->length = fresult;
        size_t count[DICT_SZ] = { 0 };
        size_t i;
        for (i = 0; i < BLK_SZ; i++)
        {
            count[src->data[i]]++;
        }
        src->length = BLK_SZ;
        for (i = 0; i < DICT_SZ; i++){
            inputs.insert(make_pair(i, count[i]));
        }
        HuffmanCode<256> hc(inputs);
        HuffmanCode::Buffer compressed(BLK_SZ + EXT_BLK_SZ);
        hc.encode(src, &compressed);
        fwrite(compressed.data, compressed.length, 1, fp_write);
        end = clock();
        //printf("%d KB processed in %d ms\n", (++blkid) * BLK_SZ / 1024, end - start);
    }
    long output_size = filelength(fileno(fp_write));
    printf("Input %ld KB, Output %ld KB, Compress rate %.2f %%\n. Total uses %d sec.", 
           input_size / 1024, output_size / 1024, (float)output_size / input_size, clock() - tstart);
    printf("Compress Finished!");
    fclose(fp_read);
    fclose(fp_write);
    getchar();
    delete src;
    return 0;
}

输入文件是一个网站MySQL导出的数据库文件，纯文本格式，共12MB左右。

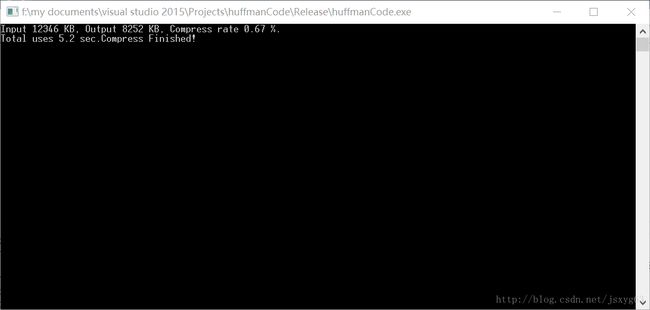
下面是程序的运行情况。压缩率为0.67，在Release X86编译下运行时间5.2s。

实际上，由于使用了分块压缩，并没有对每一块存储哈夫曼树，导致构造多个哈夫曼树压缩比反而更高一点。但是为了解压，必须存储哈夫曼树，这样每一个哈夫曼树占用的开销就不能忽视了，就必须只能存储一个哈夫曼树。存储了哈夫曼树，整个压缩效率会进一步下降。
当然这只是一个简单的玩具，不管是压缩率还是时间都是不理想的。可以在第一张图看见WinRAR普通模式压缩只有2MB不到。哈夫曼树对于每个字符均匀分布的效果并不理想，因为这种情况下，树中不同叶子结点所在的高度会相差无几，也就是所需的编码长度并不会很小。
实际上，可以改进的地方很多，比如利用OpenMP或者其他库对多核机器进行并行化加速，或者调节算法运行时间的常数提高效率，或者进一步学习利用其他更高效率的压缩算法，都是具有很大可玩性的。