【TF2.0】【笔记】神经网络小结

神经网络

感知机

感知机 Perceptron

感知机的偏置 bias

感知机的权重 weight

感知机的净活性值 z Net Activation

净活性值带入激活函数后得到活性值 Activation

激活函数可以是阶跃函数（Step function），也可以是符号函数(Sign function)

感知机存在的问题

激活函数是阶跃函数，倒数不可分

不能解决线性不可分的问题

全连接层

现代深度学习在感知机的基础上，将不连续的阶跃激活函数换成了其他平滑连续激活函数

网络层除了保存了待优化张量 trainable_variables，还有部分层包含了不参与梯度优化的张量，如后续介绍的 BatchNormalization 层，可以通过 non_trainable_variables 成员返回所有不需要优化的参数列表。如果希望获得所有参数列表，可以通过类的 variables 返 回所有内部张量列表

对于全连接层，内部张量都参与梯度优化，故 variables 返回列表与 trainable_variables 一样。

x = tf.random.normal([2, 784])
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
o1 = x @ w1 + b1
o1 = tf.nn.relu(o1)
print(o1)

fc = tf.keras.layers.Dense(256, activation=tf.nn.relu)
h1 = fc(x)
print(h1)
print(fc.bias)
print(fc.kernel)
print(fc.variables)
print(fc.trainable_variables)
print(fc.trainable_weights)

神经网络

在使用 TensorFlow 自动求导功能计算梯度时，需要将前向计算过程放置在tf.GradientTape()环境中，从而利用 GradientTape 对象的 gradient()方法自动求解参数的梯度，并利用optimizers对象更新参数

优化目标

优化的目标就是，将输入通过一个模型计算出的输出与实际值偏差，或者叫误差，这个误差一般为标量，利用数值优化方法最小化这个误差的过程

一般采用误差反向传播求解梯度信息，利用梯度下降方法迭代更新

利用误差反向传播进行反向计算的过程也叫作反向传播（BP，Backward propagation）

激活函数

Sigmoid

Sigmoid函数又叫做Logistic 函数
$$Sigmoid=\frac{1}{1+e^{-x}}$$

该函数应用可以非常广泛

可以将输出转换为概率分布

信号强度 一般可以将 0~1 理解为某种信号的强度，如像素的颜色强度，1 代表当前通道颜色最强，0 代表当前通道无颜色；抑或代表门控值(Gate)的强度，1 代表当前门控全部开放

tf.nn.sigmoid
tf.nn.relu
tf.nn.leak_relu
tf.nn.tanh

ReLU

ReLU (Rectified Linear Unit) 修正线性单元
$$ReLU(x)=max(0,x)$$

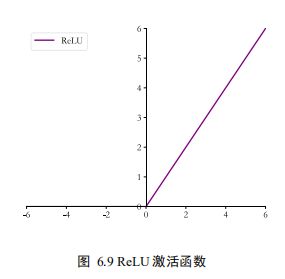
ReLU 函数的设计源自神经科学，计算十分简单，同时有着优良的梯度特性，在大量的深度学习应用中被验证非常有效，是应用最广泛的激活函数之一

LeakyReLU

为了克服ReLU梯度弥散现象提出
$$LeakyReLU=\{\begin{array}{ll}x& x\ge 0\\ p\ast x& x<0\end{array}$$

中为用户自行设置的某较小数值的超参数，如0.02 等。当 = 0时，LeayReLU 函数退化为ReLU 函数；当 ≠ 0时， < 0能够获得较小的梯度值，从而避免出现梯度弥散现象，注意这个值是要大于0的。

Tanh

ReLU的变种
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2\ast sigmoid(2x)-1$$

可以看出tanh就是sigmoid函数的放缩平移

输出层的设计

根据输出值的区间范围讨论

实数范围，比如股票预测，年龄预测

[0, 1]，像素，二分类问题

[0, 1]且和为1，分类转换为概率的问题

[-1, 1]

普通实数空间

输出可以不加激活函数，

[0, 1]

输出值[0,1]区间也比较常见，比如图片的生成，二分类问题等。在机器学习中， 一般会将图片的像素值归一化到[0,1]区间，如果直接使用输出层的值，像素的值范围会分 布在整个实数空间。为了让像素的值范围映射到[0,1]的有效实数空间，需要在输出层后添 加某个合适的激活函数，其中 Sigmoid 函数刚好具有此功能

概率问题一般结合和为1，即下面的情况

[0, 1]和为1

实现和为1的逻辑约束，可使用tf.nn.softmax
$$SoftMax=\frac{e^{z_i}}{{\sum }_{j=1}^{d_{out}}{e}^{z_j}}$$
与 Dense 层类似，Softmax 函数也可以作为网络层类使用，通过类 layers.Softmax(axis=-1)可以方便添加 Softmax 层，其中 axis 参数指定需要进行计算的维度。

在 Softmax 函数的数值计算过程中，容易因输入值偏大发生数值溢出现象；在计算交叉熵时，也会出现数值溢出的问题。为了数值计算的稳定性，TensorFlow 中提供了一个统一的接口，将 Softmax 与交叉熵损失函数同时实现，同时也处理了数值不稳定的异常，一般推荐使用，避免单独使用 Softmax 函数与交叉熵损失函数。

tf.keras.losses.categorical_crossentropy

其中 y_true 代表了one-hot 编码后的真实标签，y_pred 表示网络的预测值，当 from_logits 设置为 True 时，y_pred 表示须为未经过 Softmax 函数的变量 z；当 from_logits 设置为 False 时，y_pred 表示为经过 Softmax 函数的输出。

z = tf.random.normal([2, 10])
y_onehot = tf.constant([1,3])
y_onehot = tf.one_hot(y_onehot, depth=10)
loss = tf.keras.losses.categorical_crossentropy(y_onehot, z, from_logits=True)
loss = tf.reduce_mean(loss)
criteon = tf.keras.losses.CategoricalCrossentropy(from_logits=True)
loss1 = criteon(y_onehot, z)

[-1, 1]

简单点就是tanh函数

误差计算

均方差、交叉熵、KL 散度、Hinge Loss

均方差主要在回归问题中，也可以用于分类任务

交叉熵主要在分类问题

均方差

在TensorFlow里面可以通过函数方式和层方式实现

out = tf.random.normal([2, 10])
y = tf.constant([1, 3])
y = tf.one_hot(y, 10)
loss = tf.keras.losses.MSE(y, out)
loss = tf.reduce_mean(loss)

criteon = tf.keras.losses.MeanSquaredError()
loss2 = criteon(y, out)

交叉熵

信息学中的熵：

将热力学中的熵引入信息论，用来衡量信息的不确定度

熵在信息学科中叫信息熵，香农熵

熵越大，代表不确定性越大，信息量也就越大

某个分布P(i)的熵定义为
$$H(P)=-\sum _{i}P(i)lo{g}_{2}P(i)$$

举例：

对于四分类问题，某个样本的真实标签是第四类，one-hot编码为[0,0,0,1]，P(4)=1，不确定性为0，则熵可以计算为：
$$-0\ast lo{g}_{2}0-0\ast lo{g}_{2}0-0\ast lo{g}_{2}0-1\ast lo{g}_{2}1=0$$
如果预测的概率分布为[0.1,0.1,0.1,0.7]，熵为
$$-0.1\ast lo{g}_{2}0.1-0.1\ast lo{g}_{2}0.1-0.1\ast lo{g}_{2}0.1-0.7\ast lo{g}_{2}0.7\approx 1.7$$

交叉熵

介绍之前需要先介绍KL散度，定义为：
$$D_{KL}(p|q)=\sum _{x\in X}p(x)log(\frac{p(x)}{q(x)})$$
用于衡量两个分布的距离指标，p=q时，散度值取得最小值0，需要注意的是，交叉熵和KL散度都不是对称的，即：
$$H(p,q)\ne H(q,p)$$
交叉熵定义：
$$H(p,q)=-\sum _{i=0}p(i)lo{g}_{2}q(i)$$
可以化简为，（非常简单的化简）：
$$H(p,q)=H(p)+D_{KL}(p|q)$$
注意：

p表示的是真实标签，也就是一般用one hot编码，one hot编码的熵值为零，那么交叉熵即为真实标签y与输出之间的KL散度

接着上面的简化：
$$\begin{gathered} H(p,q)=H(y,o)=D_{KL}(y|o)=\sum _j{y}_{j}log(\frac{y_j}{o_j})=1\ast log\frac{1}{o_i}+\sum _{j\ne i}0\ast log(\frac{0}{o_j}) \\ =-lo{g}_{o_i} \end{gathered}$$
其中 i 为 onehot编码中值为1的索引号，即真实类别，可以看出，对应网络输出的预测值概率越大，交叉熵值越小，特别的，当网络输出与真实标签一致时，达到最佳状态。

故最小化交叉熵的过程也是最大化正确类别的预测概率的过程

神经网络的类型

卷积神经网络

CNN (convolutional Neural Network)

图片分类

AlexNet

VGG

GoogleNet

ResNet

DenseNet

…

目标识别

RCNN

Fast RCNN

Faster RCNN

Mask RCNN

…

循环神经网络

RNN (Recurrent Neural Network)

LSTM RNN的变种

Seq2Seq

GNMT

GRU

双向RNN

…

注意力（机制）网络

Transformer

GPT

BERT

GPT-2

图神经网络

GCN (Graph Convolution Network) 2016

GAT

EdgeConv

DeepGCN

油耗预测实战

# coding :utf-8
from __future__ import absolute_import, division, unicode_literals, print_function
import tensorflow as tf
import pandas as pd

dataset_path = tf.keras.utils.get_file("auto-mpg.data",
                                       "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")

column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight','Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,na_values = "?", comment='\t',sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
sum1 = dataset.isna().sum()
dataset = dataset.dropna()
sum2 = dataset.isna().sum()

origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1) * 1.0
dataset['Europe'] = (origin == 2) * 1.0
dataset['Japan'] = (origin == 3) * 1.0
dataset.tail()

train_dataset = dataset.sample(frac=0.8, random_state=0)
test_dataset = dataset.drop(train_dataset.index)

train_label = train_dataset.pop('MPG')
test_label = test_dataset.pop('MPG')
train_stats = train_dataset.describe()
train_stats = train_stats.transpose()

def norm(x):
    return (x - train_stats['mean']) / train_stats['std']

normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)

train_db = tf.data.Dataset.from_tensor_slices((normed_train_data.values, train_label.values))
train_db = train_db.shuffle(100).batch(32)

class Network(tf.keras.Model):
    def __init__(self):
        super(Network, self).__init__()
        self.fc1 = tf.keras.layers.Dense(64, activation=tf.nn.relu)
        self.fc2 = tf.keras.layers.Dense(64, activation=tf.nn.relu)
        self.fc3 = tf.keras.layers.Dense(1)
    def call(self, inputs, training=None, mask=None):
        x = self.fc1(inputs)
        x = self.fc2(x)
        x = self.fc3(x)
        return x

model = Network()
model.build(input_shape=(4, 9))
model.summary()
optimizer = tf.keras.optimizers.Adam(0.001)

for epoch in range(200):
    for step, (x, y) in enumerate(train_db):
        with tf.GradientTape() as tape:
            out = model(x)
            loss = tf.reduce_mean(tf.keras.losses.MSE(y, out))
            mae_loss = tf.reduce_mean(tf.keras.losses.MAE(y, out))
        if step % 10 == 0 :
            print(epoch, step, float(loss), mae_loss)
        grads = tape.gradient(loss, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

print('end')