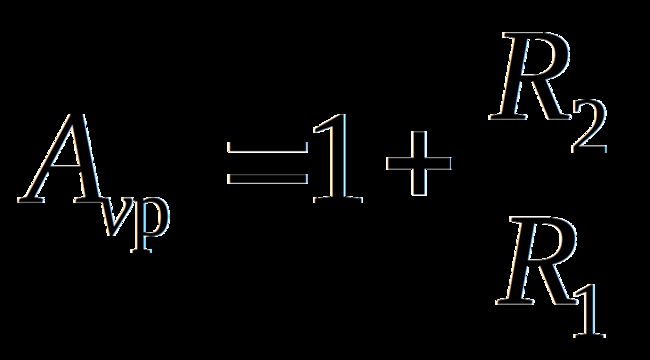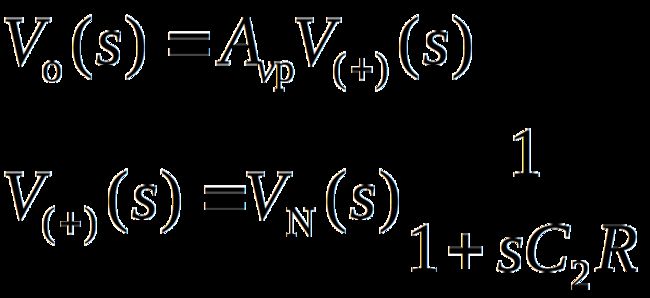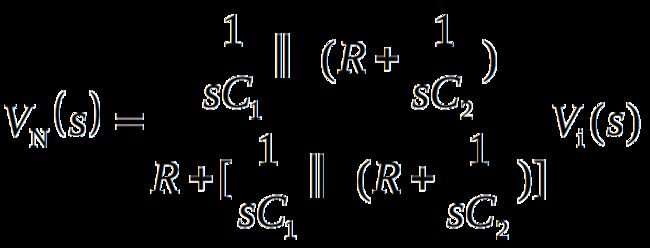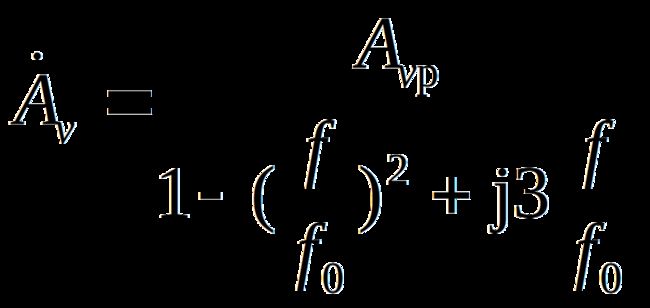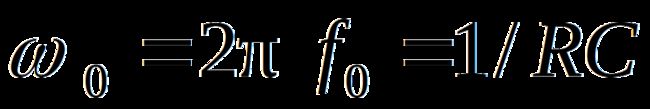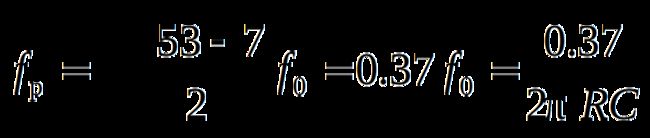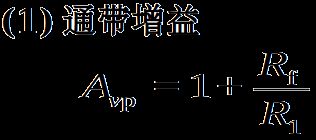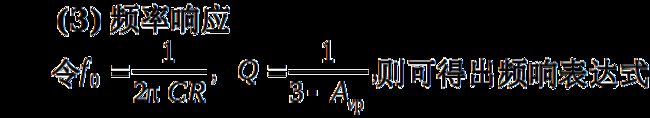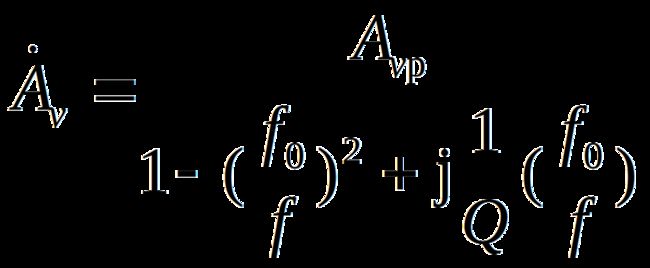滤波电路

滤波电路基本概念

  滤波的概念就是根据傅里叶分析和变换提出的一个工程概念。电信号是不同频率的正弦波线性叠加而成的，组成信号的不同频率的正弦波叫做信号的频率成分或叫做谐波成分。只允许一定频率范围内的信号成分正常通过，而阻止另一部分频率成分通过的电路，叫做滤波电路。根据高等数学理论，任何一个满足一定条件的信号，都可以被看成是由无限个正弦波叠加而成。滤波电路常用于滤去整流输出电压中的纹波，一般由电抗元件组成，如在负载电阻两端并联电容器C，或与负载串联电感器L，以及由电容，电感组成而成的各种复式滤波电路。

滤波器的分类

  有源滤波器实际上是一种具有特定频率响应的放大器。它是在运算放大器的基础上增加一些R、C等无源元件而构成的。
  通常有源滤波器分为：
    低通滤波器（LPF）
    高通滤波器（HPF）
    带通滤波器（BPF）
    带阻滤波器（BEF）

  滤波器也可以由无源的电抗性元件或晶体构成，称为无源滤波器或晶体滤波器。

滤波电路作用

滤波电路的基本作用是让某种频率的电流通过或阻止某种频率的电流通过。

滤波电路作用是尽可能减小脉动的直流电压中的交流成分，保留其直流成分，使输出电压纹波系数降低，波形变得比较平滑。
      

有源低通滤波器(LPF)

一、低通滤波器的主要技术指标

1. 通带增益Avp

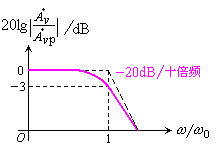
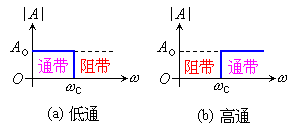
  通带增益是指滤波器在通频带内的电压放大倍数，如图所示。性能良好的LPF通带内的幅频特性曲线是平坦的，阻带内的电压放大倍数基本为零。

2.通带截止频率fp

  其定义与放大电路的上限截止频率相同。见图自明。通带与阻带之间称为过渡带，过渡带越窄，说明滤波器的选择性越好。
         

二、一阶低通有源滤波器

  一阶低通滤波器的电路如左图所示，其幅频特性见右图，图中虚线为理想的情况，实线为实际的情况。特点是电路简单，阻带衰减太慢，选择性较差。

        
当 f = 0时，各电容器可视为开路，通带内的增益为：
                

一阶低通滤波器的传递函数如下
           
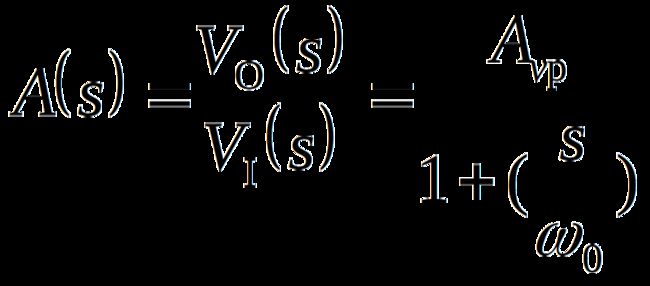
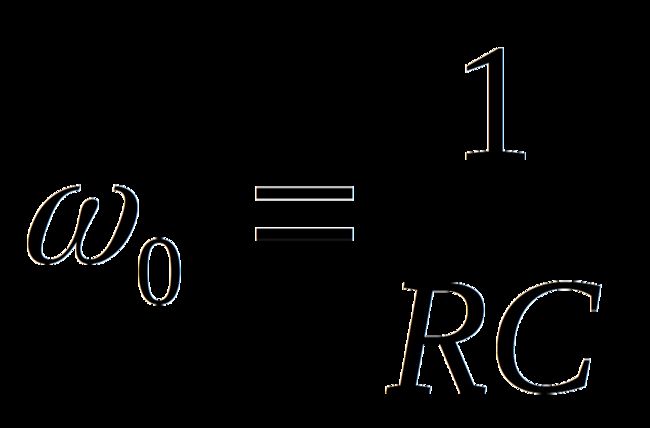
该传递函数式的样子与一节RC低通环节的频响表达式差不多，只是后者缺少通带增益Avp这一项。

三、二阶低通有源滤波器

  为了使输出电压在高频段以更快的速率下降，以改善滤波效果，再加一节RC低通滤波环节，称为二阶有源滤波电路。它比一阶低通滤波器的滤波效果更好。二阶LPF的电路图如左图所示，幅频特性曲线如右图所示。

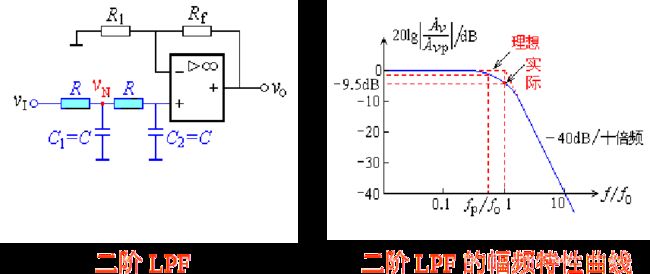
1.通带增益

当 f = 0, 或频率很低时，各电容器可视为开路，通带内的增益为
                

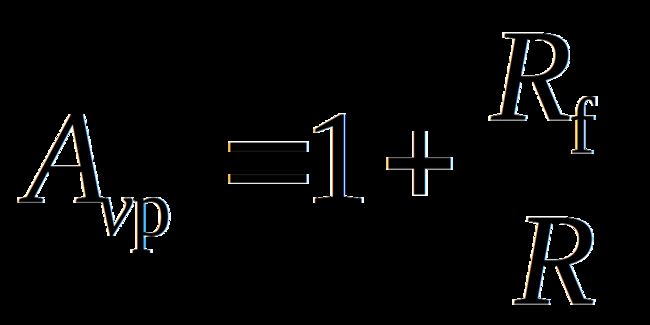
2.二阶低通有源滤波器传递函数

                
              

通常有C1=C2=C，联立求解以上三式，可得滤波器的传递函数
           

3.通带截止频率

将s换成 jω
           
当f=fp 时，上式分母的模
                
解得截止频率
             

与理想的二阶波特图相比，在超过f0以后，幅频特性以-40dB/dec的速率下降，比一阶的下降快。但在通带截止频率fp→f0之间幅频特性下降的还不够快。

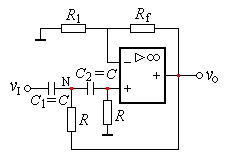
四、二阶压控型低通滤波器

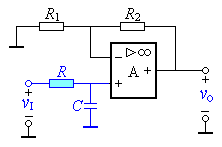
1.二阶压控LPF

  二阶压控型低通有源滤波器如左图所示。其中的一个电容器C1原来是接地的，现在改接到输出端。显然C1的改接不影响通带增益。
      

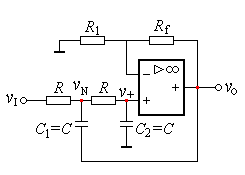
2.二阶压控型LPF的传递函数

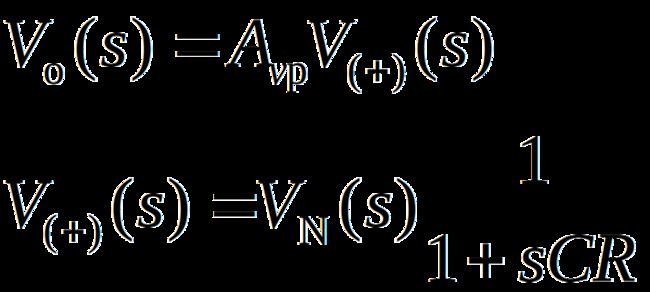
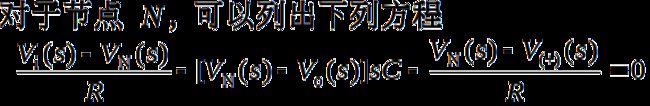
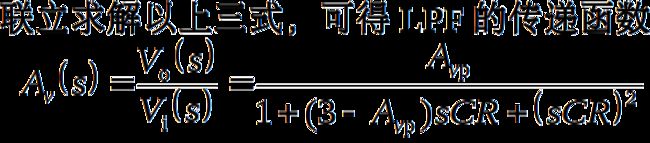
上式表明，该滤波器的通带增益应小于3，才能保障电路稳定工作。

3.频率响应

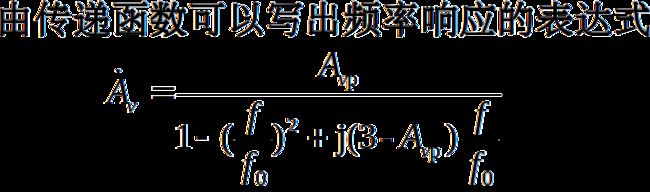
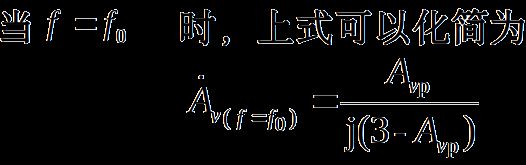
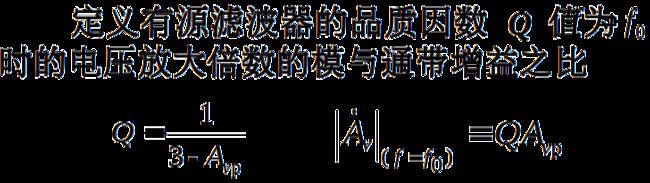
以上两式表明，当2时，Q>1，在f=f0处的电压增益将大于Avp，幅频特性在f=f0处将抬高，具体请参阅下图。当Avp≥3时，Q=∞，有源滤波器自激。由于将C1接到输出端，等于在高频端给LPF加了一点正反馈，所以在高频端的放大倍数有所抬高，甚至可能引起自激。
                

五、二阶反相型低通有源滤波器

  二阶反相型LPF如左图所示，它是在反相比例积分器的输入端再加一节RC低通电路而构成。二阶反相型LPF的改进电路如右图所示。
  




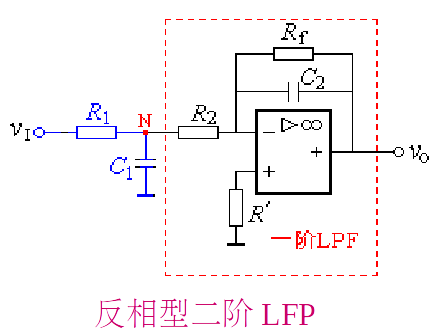
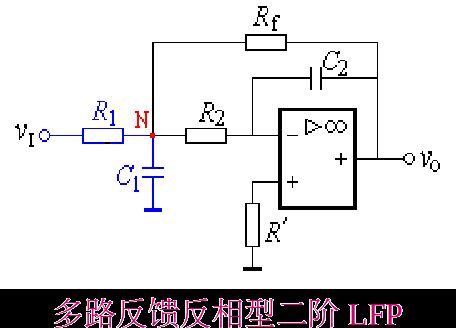
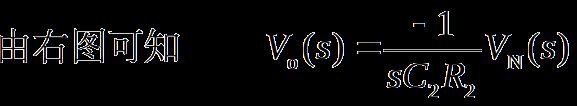
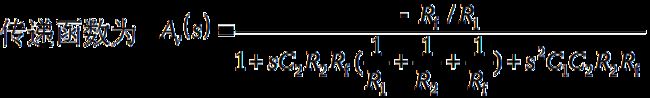
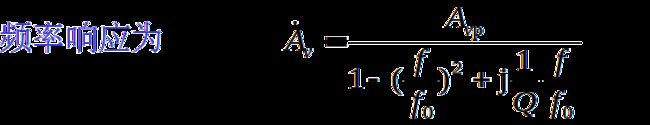
以上各式中
    

有源高通滤波器

                

由此绘出的频率响应特性曲线如下图所示
                
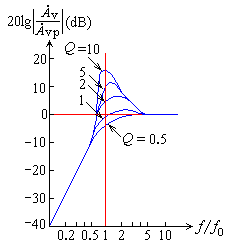
当f时，幅频特性曲线的斜率为+40dB/dec；当Avp≥3时，电路自激。

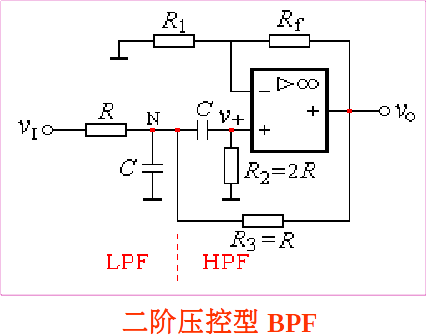
有源带通滤波器(BPF) 和带阻滤波器(BEF)

    

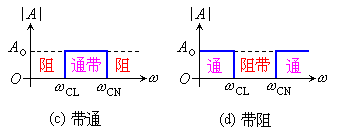
带通滤波器是由低通RC环节和高通RC环节组合而成的。要将高通的下限截止频率设置的小于低通的上限截止频率。反之则为带阻滤波器。
要想获得好的滤波特性，一般需要较高的阶数。滤波器的设计计算十分麻烦，需要时可借助于工程计算曲线和有关计算机辅助设计软件。

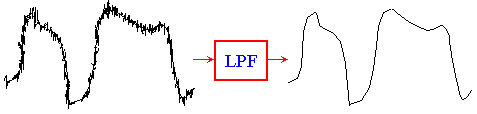
滤波器在图像处理中的应用：

理想低通滤波器、Butterworth滤波器和高斯滤波器(matlab)

参考：
http://m.elecfans.com/article/640169.html
http://m.elecfans.com/article/646402.html