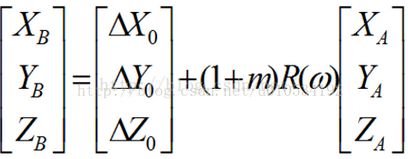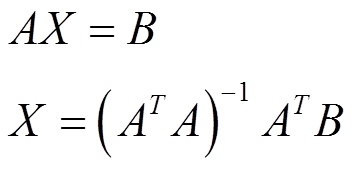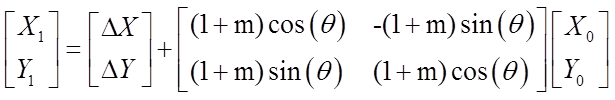空间参考(Spatial Reference)是 GIS 数据的骨骼框架,能够将我们的数据定位到相应的位置,为地图中的每一点提供准确的坐标。 在同一个地图上显示的地图数据的空间参考必须是一致的,如果两个图层的空间参考不一致,往往会导致两幅地图无法正确拼合,因此开发一个 GIS 系统时,为数据选择正确的空间参考非常重要。
1 相关知识
1.1大地水准面
大地水准面是由静止海水面并向大陆延伸所形成的不规则的封闭曲面。
1.2地球椭球体
由定义可以知大地水准面的形状也是不规则的,仍不能用简单的数学公式表示,为了测量成果的 计算和制图的需要,人们选用一个同大地水准面相近的可以用数学方法来表达的椭球体来代替, 简称地球椭球体,它是一个规则的曲面,是测量和制图的基础,因地球椭球体是人们选定的跟大 地水准面很接近的规则的曲面,所以地球椭球体就可以有多个,地球椭球体是用长半轴、短半轴 和扁率来表示的。
| 椭球名称 | 长半轴(m) | 短半轴(m) | 扁率的倒数,1/f |
| 克拉克 (Clarke 1866) | 6378 206.4 | 6356 583.8 | 294.978 8 2 |
| 贝塞尔 (Bessel 1841) | 6 377 397.155 | 6 356 078.965 | 299.152 843 4 |
| International 1924 | 6 378 388 | 6 356 911.9 | 296.999 362 1 |
| 克拉索夫斯基 (1940) | 6 378 245 | 6 356 863 | 298.299 738 1 |
| GRS 1980 | 6 378 137 | 6 356 752.3141 | 298.257 222 101 |
| WGS 1984 | 6 378 137 | 6 356 752.3142 | 298.257 223 563 |
1.3基准面
基准面是在特定区域内与地球表面极为吻合的椭球体。椭球体表面上的点与地球表面上的特定位 置相匹配,也就是对椭球体进行定位,该点也被称作基准面的原点。原点的坐标是固定的,所有其他点由其计算获得
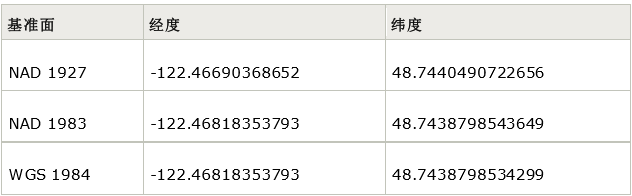
基准面的坐标系原点往往距地心有一定偏移(有的也在地心,如 WGS1984), 如西安 80 的基准面和北京 54的基准面。因为椭球体通过定位以便能更好的拟合不同的地区,所以同一个椭球体可以拟合好几个基准面.因为原点不同,所以不同的基准面上,同一个点的坐标是不相同的,这点我们应该清楚.下面以华盛顿州贝灵厄姆市为例来说明。使用 NAD27、NAD83 和 WGS84 以十进制为单位比较贝灵厄姆的坐标。显而易见,NAD83 和 WGS84 表示的坐标几乎相同,但 NAD27 表示的坐标则大不相同,这是因为所使用的基准面和旋转椭球体对地球基本形状的表示方式不同。
1.4 地图投影
简单的说地图投影就是把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法.2.
2. 两种坐标系
2.1 地理坐标系
地理坐标系也可称为真实世界的坐标系,是用于确定地物在地球上位置的坐标系,它用经纬度来表示地物的位置,经度和纬度是从地心到地球表面上某点的测量角,通常以度或百分度为单位来测量该角度。
2.2 投影坐标系
投影坐标系是基于地理坐标系的,它使用基于 X,Y 值的坐标系统来描述地球上某个点所处的位置,可以这样认为投影坐标系=地理坐标系(如:北京 54、西安 80、WGS84)+投影方法(如:高斯-克吕格、Lambert 影、Mercator 投影)+线性单位。
2.3 ArcGIS Engine 对空间参考的支持
ArcGIS Engine 提供了一系列对象供开发者管理 GIS 系统的坐标系统。对大部分开发者而言了解ProjectedCoordinateSystem, GeographicCoordinateSystem, SpatialReference Environment 这三个组件类是非常有必要的,对于高级开发者而言,可能需要自定义坐标系统可以使用这些对象Projection,Datum,AngularUnit,Spheriod,PrimeMeridian 和 GeoTransformation 等。在 ArcGIS 中除了我们上面介绍的两种坐标系,还有一种称之为 Unknown 的坐标系,这种坐标系是当我们的数据没有坐标(jpg等文件)或者坐标文件丢失的时候 ArcMap 不能识别数据的投影信息而赋予的,在 ArcGIS Engine 中下面三个类分别对应了三个坐标系:
利用 ArcGIS Engine 创 建 一 个 坐 标 系 或 者 基准面用的是SpatialReferenceEnvironmentClass 类,该类实现了 ISpatialReferenceFactory 接口,该接口 定义了创建坐标系,基准面等方法和属性。
在利用 ISpatialReferenceFactory 创建坐标系的时候往往需要一个 int 类型的参数,这个int 其实就是这些坐标系的代号,如我们熟悉的 4326 就是 WGS1984。
2.4 同一基准面的坐标转换
对于同一基准面,我们可以肯定一点就是同一位置经纬度坐标是一样的,而不同的就是计算成平面坐标的时候可能有所不同,因为算法不一样,在这里我只是将经纬度坐标转成平面的坐标。
// 同一椭球下经纬度坐标、平面的坐标互转
private IPoint GetpProjectPoint(IPoint pPoint, bool pBool) { ISpatialReferenceFactory pSpatialReferenceEnvironemnt = new SpatialReferenceEnvironment(); ISpatialReference pFromSpatialReference = pSpatialReferenceEnvironemnt.CreateGeographicCoordinateSystem((int)esriSRGeoCS3Type.esriSRGeoCS_Xian1980);//西安80 ISpatialReference pToSpatialReference = pSpatialReferenceEnvironemnt.CreateProjectedCoordinateSystem((int)esriSRProjCS4Type.esriSRProjCS_Xian1980_3_Degree_GK_Zone_34);//西安80 if (pBool == true)//球面转平面 { Geometry pGeo = (IGeometry)pPoint; pGeo.SpatialReference = pFromSpatialReference; pGeo.Project(pToSpatialReference); return pPoint; } else //平面转球面 { IGeometry pGeo = (IGeometry)pPoint; pGeo.SpatialReference = pToSpatialReference; pGeo.Project(pFromSpatialReference); return pPoint; } }
2.5 不同基准面的坐标转换
2.5.1 三参数与七参数
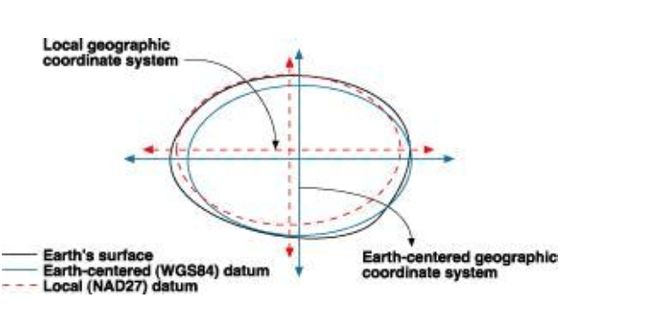
通过前面的介绍,我们知道地球上同一位置的坐标在不同的基准面上是不一样的,而基准面是构成坐标系的一个部分,因为基准面在定位的时候牵扯到了相对地心的平移或旋转等,所以对于这样的转换我们无法直接进行,需要一个转换参数,而这些参数也是基于不同的模型的,常用的有三参数和 7 参数,三参数是比较简单的也是比较容易理解的,三参数是在两个基准面之间进行了 X, Y, Z 轴的平移,通过下面的图我们很清楚的看到三参数之间两个基准面的关系:
如果知道了这三个平移的参数(dx, dy, dz),外加1个基准面上的点,那么:
而 7 参数的模型比较复杂,这种复杂的同时让精度大为提高,7参数不仅仅考虑了两个基准面之间的平移,还考虑了旋转外加一个比例因子(椭球体的大小可能不一样).
空间直角坐标系(XYZ) 转换(To) 空间直角坐标系(XYZ):(布尔沙模型,此步重要,将一个椭球基准转换到另一个椭球基准)
7参数转换整体流程(不同椭球之间):
举个栗子,比如从BJ1954平面直角坐标系 转到WGS84平面直角坐标系那么需要5步:
①BJ1954平面直角坐标系 至 BJ1954大地坐标系
②BJ1954大地坐标系 至BJ1954空间直角坐标系
③BJ1954空间直角坐标系 至WGS84空间直角坐标系
④WGS84空间直角坐标系 至WGS84大地坐标系
⑤WGS84大地坐标系 至WGS84平面直角坐标系
如果从BJ1954空间直角坐标系转到WGS84平面直角坐标系只需一步:
①BJ1954空间直角坐标系 至 WGS84空间直角坐标系
2.5.2 最小二乘法求解七、四参数
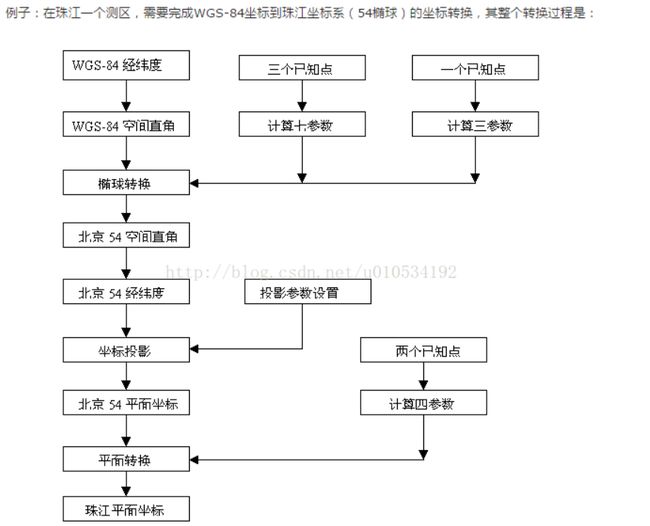
2.5.3 DEMO坐标转换的整体流程
2.5.4 七参数的ArcGIS编程实现
对于不同基准面之间的转换,ArcGIS Engine 提供了一个用来控制转换参数的接口 IGeoTransformation,该接口被被较多的其它类实现着。
每一个接口对应了一种转换方法,比如 GeocentricTranslationClass类就实现了三参数,而CoordinateFrameTransformationClass 类实现了7 参数,要实现 3 参数或者 7 参数需要 IGeometry2 或更新接口的ProjectEx 方法,下面我们用代码实现一个不同基准面之间的坐标转换。
// 不同基准面之间的坐标转换 WGS1984 GaussKruger -- > esriSRProjCS_Xian1980_GK_Zone_19
public void ProjectExExample() { ISpatialReferenceFactory pSpatialReferenceFactory = new SpatialReferenceEnvironmentClass(); // ISpatialReference pFromCustom = pSpatialReferenceFactory.CreateESRISpatialReferenceFromPRJFile(@"E:\arcgis\Engine\z idingyi.prj");
IPoint pFromPoint = new PointClass(); pFromPoint.X = 518950.788; pFromPoint.Y = 4335923.97; IZAware pZAware = pFromPoint as IZAware; pZAware.ZAware = true; pFromPoint.Z = 958.4791; // 自定义投影WGS84下的北京6度 19带。 ((IGeometry)pFromPoint).SpatialReference = CreateCustomProjectedCoordinateSystem(); // ((IGeometry)pFromPoint).SpatialReference = pFromCustom;
//目标投影 IProjectedCoordinateSystem projectedCoordinateSystem = pSpatialReferenceFactory.CreateProjectedCoordinateSystem((int)esriSRProjCS4Type.esriSRProjCS_Xian1980_GK_Zone_19); //因为目标基准面和原始基准面不在同一个上,所以牵扯到参数转换,我用7参数 转换 ICoordinateFrameTransformation pCoordinateFrameTransformation = new CoordinateFrameTransformationClass(); pCoordinateFrameTransformation.PutParameters(-112.117, 4.530, 21.89, -0.00058702, -0.00476421, 0.00009358, 0.99998006411); pCoordinateFrameTransformation.PutSpatialReferences(CreateCustomProjectedCoordinateSystem(), projectedCoordinateSystem as ISpatialReference);
//投影转换 IGeometry2 pGeometry = pFromPoint as IGeometry2; pGeometry.ProjectEx(projectedCoordinateSystem as ISpatialReference, esriTransformDirection.esriTransformForward, pCoordinateFrameTransformation, false, 0, 0); } private IProjectedCoordinateSystem CreateCustomProjectedCoordinateSystem() { ISpatialReferenceFactory2 pSpatialReferenceFactory = new SpatialReferenceEnvironmentClass(); IProjectionGEN pProjection = pSpatialReferenceFactory.CreateProjection((int)esriSRProjectionType.esriSRProjection_GaussKruger) as IProjectionGEN;
IGeographicCoordinateSystem pGeographicCoordinateSystem = pSpatialReferenceFactory.CreateGeographicCoordinateSystem((int)esriSRGeoCSType.esriSRGeoCS_WGS1984); ILinearUnit pUnit = pSpatialReferenceFactory.CreateUnit((int)esriSRUnitType.esriSRUnit_Meter) as ILinearUnit; IParameter[] pParameters = pProjection.GetDefaultParameters();
IProjectedCoordinateSystemEdit pProjectedCoordinateSystemEdit = new ProjectedCoordinateSystemClass(); object pName = "WGS-BeiJing1954"; object pAlias = "WGS-BeiJing1954"; object pAbbreviation = "WGS-BeiJing1954"; object pRemarks = "WGS-BeiJing1954"; object pUsage = "Calculate Meter From lat and lon"; object pGeographicCoordinateSystemObject = pGeographicCoordinateSystem as object; object pUnitObject = pUnit as object; object pProjectionObject = pProjection as object; object pParametersObject = pParameters as object; pProjectedCoordinateSystemEdit.Define(ref pName, ref pAlias, ref pAbbreviation, ref pRemarks, ref pUsage, ref pGeographicCoordinateSystemObject,
ref pUnitObject, ref pProjectionObject, ref pParametersObject); IProjectedCoordinateSystem5 pProjectedCoordinateSystem = pProjectedCoordinateSystemEdit as IProjectedCoordinateSystem5; pProjectedCoordinateSystem.FalseEasting = 500000; pProjectedCoordinateSystem.LatitudeOfOrigin = 0; pProjectedCoordinateSystem.set_CentralMeridian(true, 111); pProjectedCoordinateSystem.ScaleFactor = 1; pProjectedCoordinateSystem.FalseNorthing = 0;
return pProjectedCoordinateSystem; }
参考文章
坐标转换流程与公式 七参数 四参数,2017.8.15.
ArcGIS E0ngine开发之旅10--空间参考及坐标转换,2016.8.4
在ArcGIS Desktop中进行三参数或七参数精确投影转换
墨卡托投影、高斯-克吕格投影、UTM投影及我国分带方法
地图投影与ArcGIS坐标系转换
地理坐标系、大地坐标系与地图投影与重投影详解
安卫. 一种平面四参数法坐标转换方法的实现, 2012.