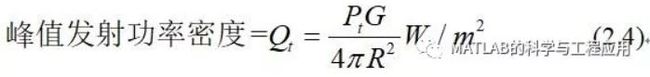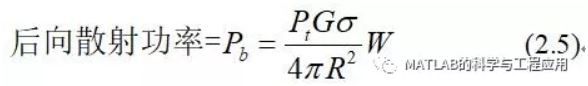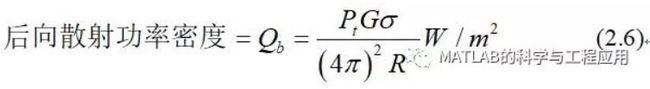【读书2】【2014】基于MATLAB的雷达信号处理基础（第二版）——简单点目标的雷达距离方程(1)

2.2. 幅度

2.2. Amplitude

2.2.1. 简单点目标的雷达距离方程

2.2.1. Simple Point Target Radar RangeEquation

雷达距离方程(Richards等人，2010；Skolnik，2001)是一个确定性模型，它根据各种系统设计参数将接收的回波功率与发射功率联系起来。

The radar range equation (Richards et al.,2010; Skolnik, 2001) is a deterministicmodel that relates received echo power to transmitted power in terms of avariety of system design parameters.

它是用于基本系统设计和分析的基础关系表达式。

It is a fundamental relation used for basicsystem design and analysis.

由于接收回波信号是式(2.2)形式的窄带脉冲，所以由距离方程估计的接收功率Pr可以直接与接收的脉冲幅度相关。

Since the received signals are narrowbandpulses of the form of Eq. (2.2), the received power Pr estimated bythe range equation can be directly related to the received pulse amplitude.

为了推导距离方程，假设各向同性辐射单元将功率Pt瓦的波形辐射到无损介质中。

To derive the range equation, assume thatan isotropic radiating element transmits a waveform of power Ptwatts into a lossless medium.

因为传输是各向同性的，并且在介质中没有功率损失，所以R距离处的功率密度为总功率Pt除以半径为R的球体表面积，即

Because the transmission is isotropic andno power is lost in the medium, the power density at a range R is the totalpower Pt divided by the surface area of a sphere of radius R, whichis

实际的雷达系统使用定向天线来聚焦输出的能量，而不是采用各向同性的辐射器。

Instead of isotropic radiators, real radarsuse directive antennas to focus the outgoing energy.

如第一章所述，天线增益G是最大功率密度与各向同性功率密度之比。

As described in Chap. 1, the antenna gain Gis the ratio of maximum power density to isotropic density.

因此，在最大辐射强度的方向上，距离R处的功率密度为

Thus, in the direction of maximum radiationintensity, the power density at range R becomes

这是入射到目标上的功率密度，前提是目标与天线的最大增益方向是对准的。

This is the power density incident upon thetarget if it is aligned with the antenna’s axis of maximum gain.

当式(2.4)给出的具有功率密度的电磁波在距离R处入射到单个离散散射物体或点目标上时，入射能量在各个方向上产生散射，其中一些能量也可能被散射体本身吸收。

When the electromagnetic wave with powerdensity given by Eq. (2.4) is incident upon a single discrete scatteringobject, or point target, at range R the incident energy is scattered in variousdirections; some of it may also be absorbed by the scatterer itself.

特别地，一些入射功率被重新反射回雷达，或者产生后向散射。

In particular, some of the incident poweris reradiated toward the radar, or backscattered.

假设目标收集所有入射到面积σ平方米上的电磁波能量，然后再各向同性地重新辐射出去。

Imagine that the target collects all of theenergy incident upon a collector of area σ square meters and reradiates itisotropically.

再次辐射的能量为

The reradiated power is then

σ被称为目标的雷达散射截面（RCS）。

The quantity σ is called the radar crosssection (RCS) of the target.

关于RCS的一个重要事实是，σ不等于目标的物理截面积；它是一个等效的面积，可以用来将目标处的入射功率密度与在接收机处产生的反射功率密度相关联。

One important fact about RCS is that σ isnot equal to the physical cross-sectional area of the target; it is anequivalent area that can be used to relate incident power density at the targetto the reflected power density that results at the receiver.

将在第2.2.3节中进一步讨论RCS的概念。

RCS will be discussed further in Sec. 2.2.3.

因为RCS是在假设后向散射功率各向同性地再次辐射下定义的，所以通过将式(2.5)的功率除以半径为R的球体表面积，求得在R距离处的后向散射功率密度，如式(2.3)中所做的那样，给出雷达接收机处的后向散射功率密度为

Because RCS is defined under the assumptionthat the backscattered power is reradiated isotropically, the density of thebackscattered power at a range R is found by dividing the power of Eq. (2.5) bythe surface area of a sphere of radius R as was done in Eq. (2.3), giving thebackscattered power density at the radar receiver as

——本文译自Mark A. Richards所著的《Fundamentals of Radar Signal Processing（Second edition）》

更多精彩文章请关注微信号：