牛客寒假算法基础集训营6学习笔记

出题

题目描述
小B准备出模拟赛。 她把题目按难度分为四等，分值分别为6,7,8,9。 已知小B共出了m道题，共n分。
求小B最少出了多少道6分题。

输入描述:
两个正整数n,m

输出描述:
一个数，表示答案。 若无解，输出"jgzjgzjgz"。

一道数学题；
首先可以判断出一种显然无解的情况，即总分大于全为9分或总分小于全为6分。
由此可以得到启发，我们可以枚举全取某一道题的情况，得出该情况的总分，与实际总分对比。比如按照样例，我们全取7分的话，是35分，而实际是34分，很明显的必须出现一道6分题，才能取到34分。

由此，做法就明确了，当总分大于等于全取7分时就为0道，小于时做差即可，无解的情况早已给出（上方）

代码如下（注意数据范围。。。）

#include 
using namespace std;
int main()
{
    long long n,m;
    cin >> n >> m;
    if((n9*m))cout << "jgzjgzjgz" << endl;
    else if(n>=7*m)cout << 0 << endl;
    else cout << (m*7)-n << endl;
    return 0;
}

煤气灶

题目描述
小j开始打工，准备赚钱买煤气灶。 第一天，小j的工资为n元，之后每天他的工资都比前一天多d元。
已知煤气灶需要m元，求小j最少工作几天才能买到煤气灶。

输入描述:
四个整数 n,m,d,x 分别表示小j第一天的工资，煤气灶的价格，工资每天的增长量，答案不超过x

输出描述:
一个数表示答案

又是一道数学题 解二元一次不等式，用二分法确定（暴力好像不行。。。）

代码如下：

#include 
using namespace std;
long long n,d,x,m;
long long fun(long long g)
{
    return d*g*g+(2*n-d)*g-2*m;
}
int main()
{
    int h,r,l;
    cin >> n >> m >> d >> x;
    r=1,l=x;
    h=(r+l)/2;
    while(1)
    {
        h=(r+l)/2;
        if(fun(h)<0)r=h;
        else l=h;
        if(fun(h-1)<0&&fun(h)>=0)break;
    }
    //cout << fun(h) << ' ' << fun(h-1) << endl;
    cout << h << endl;
    return 0;
}

项链

题目描述
小B想给她的新项链染色。 现在有m种颜色，对于第i种颜色，小B有a_i单位的颜料，每单位颜料可以染项链的一个珠子；
同时，小B对于第i种颜色的喜爱度为b_i。 已知项链有n个珠子，求染色后每个珠子的颜色的喜爱度之和的最大值。
(每个珠子只能至多被染一次，不被染色则喜爱度为0)

输入描述:
第一行两个数n,m 第二行m个数a_i 第三行m个数b_i

输出描述:
一个数表示答案

个人觉得是最简单的一道了，贪心；
优先染喜爱度高的即可，唯一的知识点是结构体的排序，自己写一个cmp函数即可；

代码如下：

#include 
using namespace std;
struct zhuzi
{
    int a,b;
}z[100001];
bool cmp(zhuzi x,zhuzi y)
{
    return x.b>y.b;
}
int main()
{
    int n,m;
    long long ans=0;
    cin >> n >> m;
    for(int i=0;i> z[i].a;
    }
    for(int i=0;i> z[i].b;
    }
    sort(z,z+m,cmp);
    for(int i=0;i=z[i].a)n-=z[i].a,ans+=z[i].a*z[i].b;
        else {ans+=n*z[i].b;break;}
    }
    cout  << ans << endl;
    return 0;
}

美食

题目描述
小B喜欢美食。 现在有n个美食排成一排摆在小B的面前，依次编号为1…n，编号为i的食物大小为 a[i] ，即足够小B吃
a[i] 口。 小B每次会吃两口，这两口要么是编号相同的美食，要么是编号之差的绝对值为1的美食。 小B想知道，她最多能吃几次？

输入描述:

第1行一个正整数n，表示美食个数 接下来n行，第i行一个整数a[i]，表示编号为i的美食的大小

输出描述:

一个数表示小B最多吃几次。

应该来说是一道思维题；
最优的情况是全部不浪费，则此时可以吃的次数一定是最多的，因为你都吃下去了（或者剩一个）

那么就是一个凑偶数的问题，想法是遍历整个数组，如果当前遍历到的数字不为偶数，那么我们可以把后面的一个数字（如果有的且不为0话）分一个1给该数凑成偶数，最后再遍历一遍数组每次除以2然后将总数加起来即可；

代码如下：

#include 
using namespace std;
const int mx=100001;
int fo[mx];
int main()
{
    int n,flag=0;
    long long ans=0,zans=0;
    cin >> n;
    for(int i=0;i> fo[i];
        if(fo[i-1]%2==1&&i>0&&fo[i]!=0)fo[i-1]++,fo[i]--;
    }
    for(int i=0;i

海啸

考点：二维前缀和，动态分配内存，输入输出的问题；

1：n次询问一个区间内的和，很容易想到前缀和；那么这就是一个二维前缀和的问题；
盗的别人的一个图。。。
很明显的是N（x1,y1）到N(x2,y2)的一个范围等于N(x2,y2)-N(x2,y1-1)-N(x1-1,y2)+N(x1-1,y1-1);

至于二维前缀和如何生成，方法多多，你可以二重循环加一次或者读入的时候直接预处理一下。

2：另外一个问题该题保证n*m<=1e6，但是为了保证可以包含所有情况理论上是应该建立一个1e6*1e6的数组的，然而这会爆掉；所以，我们要用到动态内存分配；

3：这题输入输出用cout/cin会超时，必须用printf/scanf，或者ios::sync_with_stdio(false/0)；

代码如下：

#include 
using namespace std;
const int mx = 1e6 + 1;
int *nu[mx];
int main()
{
    ios::sync_with_stdio(false);
	int n, m, d, q;
	long long ans = 0;
    //scanf("%d%d%d",&n,&m,&d);
	cin >> n >> m >> d;
	for (int i = 0; i <= n; i++) { nu[i] = new int[m + 1];for (int j = 0; j < m + 1; j++)nu[i][j] = 0;};
    //动态内存分配+初始化
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			int x;
			//scanf("%d",&x);
			cin >> x;
            nu[i][j] = nu[i][j - 1] + nu[i - 1][j] - nu[i - 1][j - 1] + (x >= d);//生成二维前缀和
		}
	}
	cin >> q;
	while(q--)
	{
		int x1, y1, x2, y2;
		//scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        cin >> x1 >> y1 >> x2 >> y2;
		//printf("%d\n",nu[x2][y2] + nu[x1 - 1][y1 - 1] - nu[x2][y1 - 1] - nu[x1 - 1][y2]);//求区间值
	    cout << nu[x2][y2] + nu[x1 - 1][y1 - 1] - nu[x2][y1 - 1] - nu[x1 - 1][y2] << endl;
    }
	for (int i = 0; i <= n; i++)delete nu[i];//好习惯。。。。
	//system("pause");
	return 0;
}

石头剪刀布

递归+思维；
这题的思路实际上是一个倒推的思想，即如果我知道了获胜者，那么比赛的两个人也就知道了。

所以，我们可以通过枚举获胜者的偏好根据R、P、S的数量和（用来确定递归层数）来最终确定整个序列；

大概是这样一个倒推过程。。。

然后字典序的问题具体看代码：

#include 
#include 
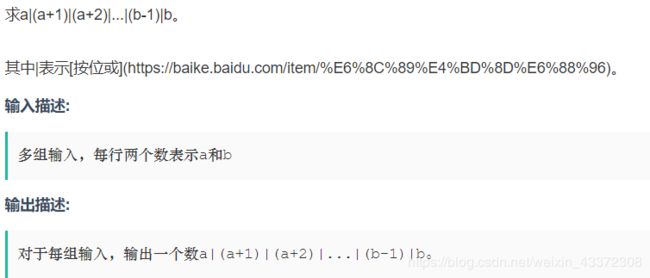
#include 

区间或和

该题考的是位运算，如果比较熟位运算的话也是一道简单题；
那么有b大于a，那么a在向b趋近的过程会把b的后几位全部变成1（或运算）
例： b=1101001(105)与a=1100000(96)；那么很明显最后结果是1101111(111)，后面的几位全部变成1；

于是题目就转化为在a~b之间会新出现多少个1；

做法就是枚举1出现的位数，看它与a的和的大小是否小于b之间，如果在就 或一下 最后输出最终值

代码如下：

#include 
using namespace std;
int main()
{
    long long x,y,m,n;
    while(~scanf("%lld%lld",&x,&y))
    {
        m=x|y;
        long long t=1;
        while(t<=y)//不停枚举1的位数
        {
            if(x+t<=y)m|=t;//符合条件就 或运算
            t<<=1;//1左移一位
        }
        cout << m << endl;
 
    }
    return 0;
}

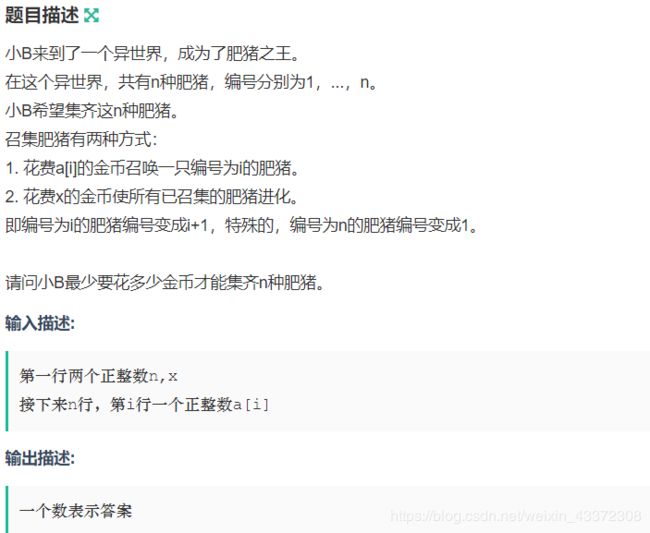
肥猪

该题的算是一道隐藏的贪心题，较为复杂。。。
知识点：区间最小值可以由单调队列来实现；
一只序号为i的肥猪，我们可以直接a[i]召唤，也可以通过召唤i-n的肥猪再升格n次来得到；

那么很显然的是，对于一只肥猪在确定了升格次数（n）时的最小召唤代价应为i~i-n的一个区间内的最小值；

为什么不能直接对每个肥猪取整个区间的最小值是因为升格次数是对全体有效的，换句话说对于某个肥猪取到了最小召唤代价不代表全体也能取到最小召唤代价；

因此正确的做法是枚举升格次数，对每个肥猪取确定升格次数内的最小值，然后求和来比较；

区间最小值由（单调）队列来实现；

代码如下：

#include 
#include 
#include 
#include 
using namespace std;
const int mx = 4010;
int a[mx];
dequeq;
void push(int j)
{
	while (!q.empty() && a[q.back()] >= a[j])q.pop_back();//保证队列处于一种从小到大的顺序
	q.push_back(j);
}
int main()
{
	int n, x;
	cin >> n >> x;
	for (int i = 1; i <= n; i++)cin >> a[i];
	for (int i = n + 1; i <= 2 * n; i++)a[i] = a[i - n];//多复制一组a，做越界处理；
	long long ans = 1e16;
	for (int i = 0; i < n; i++)
	{
		long long now = 0;
		q.clear();
		for (int k = n + i; k >= n + 1; k--)push(k);//提前将可能多出来的部分压到队列里
		for (int j =n ; j >=1 ; j--)
		{
			push(j);//将当前序列对应的价值压入队列
			while (!q.empty() && q.front() > j + i)q.pop_front();//保证队列的最小值可以被取到；
			now += a[q.front()];
		}
		ans = min(ans, now + i * (long long)x);
	}
	cout << ans << endl;
	//system("pause");
	return 0;
}

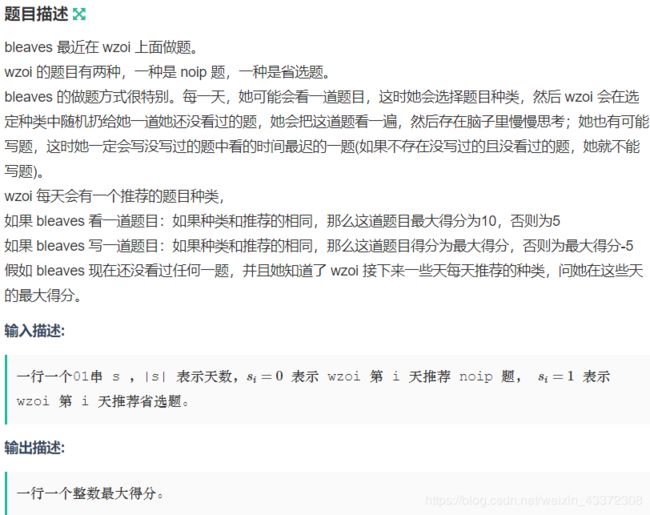
wzoi

贪心
题意比较复杂，如果我们认为00/11是一个完美二元组的话，那么当完美二元组直接出现，或两个完美二元组的组成元素中间只有若干个类似的完美二元组的时候
（例：1001属于完美二元组，10100101也是完美二元组）
可以取到10，否则都是取到5；

所以做法就是把完美二元组删去，留下的就全是只能取到5的部分，直接/2*5即可

代码如下：

#include 
using namespace std;
string x,y;
int main()
{
    cin >> x;
    for(auto c : x)//遍历字符串
    {
        if(y.empty()||y.back()!=c)y.push_back(c);//不出现完美二元组就让它入队
        else y.pop_back();//出现完美二元组就删去
        //最后y就是全部不含完美二元组的情况
    }
    printf("%d\n",(x.size()-y.size()/2)*5);
    return 0;
}

迷宫

bfs（广度优先搜索）
一看就是bfs，dfs（深度优先搜索）估计也能做不过太麻烦而且不保险；
我的做法是优先队列，不过好像不用优先队列也可以做出来；

引用官方题解的话（针对一个格子你可以直接判断它能否被到达）

代码如下:

#include 
#include 
using namespace std;
int n,m;
const int mx=1001;
int mo[4][2]={{-1,0},{0,1},{1,0},{0,-1}},ans=0;
int vis[mx][mx]={0};
char mg[mx][mx];
struct node
{
    int x,y,l,r;
    bool operator < (const node & a) const//重载小于号，优先队列的关键
	{
		return r+lq;
void bfs()//标准的bfs
{
    while(!q.empty())
    {
        node h=q.top();
        ans++;
        //cout << h.x << h.y << endl;
        for(int i=0;i<4;i++)
        {
            int x1=h.x+mo[i][0]
                ,y1=h.y+mo[i][1];
            if((x1>=0)&&(x1=0)&&(vis[x1][y1]==0)&&(mg[y1][x1]!='*')&&(!((i==0&&h.l==0)||(i==2&&h.r==0))))
            {
                vis[x1][y1]=1;
                if(i==0)q.push(node{x1,y1,h.l-1,h.r});
                else if(i==2)q.push(node{x1,y1,h.l,h.r-1});
                else q.push(node{x1,y1,h.l,h.r});

            }
        }
        q.pop();
    }
}
int main()
{
    cin >> n >> m;
    node o;
    cin >> o.y >> o.x >> o.l >> o.r;
    o.x--,o.y--;
    vis[o.x][o.y]=1;
    q.push(o);
    getchar();
    for(int i=0;i