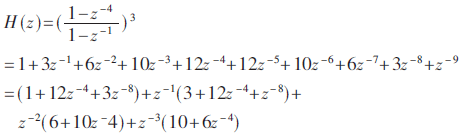如何利用CIC滤波器、CIC补偿滤波器和半带滤波器设计一个高频数字抽取滤波器

设计了采样频率为640 MHz、过采样率为64的 高频 数字抽取 滤波器。该数字抽取滤波器由 CIC（Cascaded Integrator Comb）滤波器（降16倍）、CIC补偿滤波器（降2倍）和半带滤波器（降2倍）组成。为了实现高频工作，CIC滤波器采用两级结构，第一级采用多相分解技术，使大部分结构工作在较低时钟频率下，极大地降低了CIC的功耗，第二级采用传统结构。CIC补偿滤波器使信号通带平坦，半带滤波器满足了阻带的衰减要求。为了验证数字滤波器的性能，搭建了四阶前馈—反馈结构ΣΔ调制器，作为数字抽取滤波器的输入，最终在输入信号频率为0.5 MHz时，数字抽取滤波器输出的信噪比为97.40 dB。

 

0 引言

数字抽取滤波器是ΣΔADC(ΣΔAnolog-to-Digital Converter)的重要组成部为分，旨在从高速、低分辨率的调制信号中重构出高分辨率、奈奎斯特频率的信号。为节约硬件资源，同时满足通带纹波和阻带衰减等要求，数字抽取滤波器一般采用CIC滤波器、CIC补偿滤波器、半带滤波器三级级联方式构成[1]。本文在此结构的基础上，对CIC滤波器部分进行优化，通过级联结构和多相分解技术，最终有效地降低了CIC滤波器的功耗，提升了滤波器的运算速度。

 

为更好地验证数字抽取滤波器的性能，本设计的输入信号由ΣΔ调制器产生。根据640 MHz采样频率和64倍降采样率，计算得到调制器最小阶数为四阶。经过单环、级联结构的对比分析，最终选用四阶单环前馈-反馈ΣΔ调制器。即在单环ΣΔ调制的基础上，将第四级积分器的输入和输出端分别引入前馈和反馈，同时让反馈回路作为第三级积分器的输入[2]。在MATLAB中，使用0.5 MHz信号对该调制器进行验证，调制器的输出信噪比为114.7 dB。

 

本设计的数字抽取滤波器的目标参数为：信号带宽5 MHz，输入信号频率0.5 MHz，采样频率640 MHz，过采样率为64，输出信噪比90 dB以上，通带纹波不大于0.01 dB。

 

1 CIC滤波器的设计

1.1 传统CIC滤波器

CIC抽取滤波器是一种线性相关的FIR(Finite Impulse Response，FIR)滤波器，滤波器系数均为1，结构组成只有积分器、寄存器和加法器，省去了乘法器，有效降低了硬件开销和电路复杂度。

 

降采样率为M，阶数为N的CIC滤波器的z域传输函数为[3]：

 

 

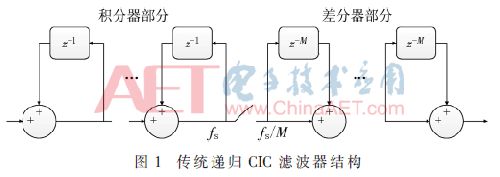
根据传输函数得到图1的滤波器结构图，此为传统递归结构。

 

 

传统结构的CIC滤波器由两部分组成：第一部分为积分器，第二部分为差分器。可以看到，所有积分器都工作在最高采样频率下，导致了传统结构功耗的增加。

 

芯片版图尺寸主要由寄存器个数及位数决定,字长大消耗硬件资源多,所以CIC滤波器的输出数据位数增长也是需要关注的一个方面。降采样率为M，阶数为N的CIC滤波器输出数据位数由Nlog2M+Bin决定，Bin为调制器输入位数。

 

1.2 多相分解CIC滤波器

为有效降低功耗，应使滤波器工作在低采样频率下，即让抽取步骤在整个CIC滤波器的最前端完成，这就需要对CIC滤波器的传输函数进行多相分解[4]。

 

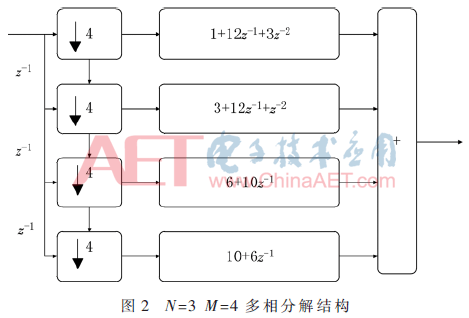
下面以N=3、M=4为例，对分解步骤进行说明，由分解后的图2可得采样频率降低为fs/4。

 

 

该结构中的系数相乘可以通过移位相加实现，因此只需要延时器（寄存器）和加法器，消耗资源少。通过多相分解，在一开始就进行降采样，使后级都工作在较低的时钟频率下，有效降低了功耗。

 

 

1.3 CIC滤波器的结构设计

为使量化噪声在信号带宽内的混叠可以忽略不计，对于L阶的ΣΔ调制器，CIC滤波器至少为L+1阶。由四阶调制器可得，本次设计应至少选用五阶CIC滤波器来实现16倍降采样。

 

将其分为两级4×4级联结构以避免一级结构过于复杂，根据Noble恒等式得：

 

 

由于第一级选择多相结构，p选取2或者3。再参考幅频特性以及占用资源来选出最佳q值。

 

1.3.1 幅频特性分析

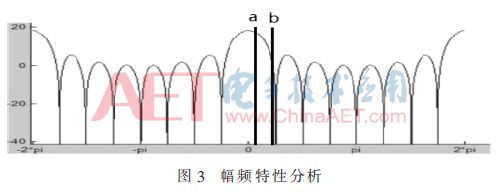
幅频特性主要看混叠带部分的衰减情况，因为这部分决定了总体的噪声情况。如图3，线a处对应通带截止频率，线b处对应混叠发生区域。引入带宽比例因子β=B/Fs×M=5/640×16=1/8，计算得到a处的值为w1=β×2×π/16，b处的值为w2=2×π/16-w1。对w1、w2归一化处理后得w1′=w1/π=0.015 6，w2′=w2/π=0.109 4。

 

 

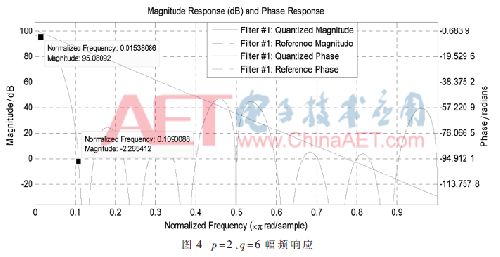
p=2时，q最小取值为6，现选取q=6、7、8进行比较，使用不同的q值进行级联，得到对应幅频响应图，如图4所示。观察位于w1′、w2′处的衰减情况。表1为p=2时的通带和阻带衰减对比。

 

 

由表1可知第二级取值越大，混叠处的衰减越大，但同时基带内信号的衰减也会增加，影响幅频特性。当q=7时，混叠处的衰减已经满足要求，所以p=2时，对应选取q=7。

 

同理p=3，q分别取6、7、8时，对应混叠区域的衰减情况见表2。

 

 

经过比较，选择3-6结构或2-7结构。

 

1.3.2 加法器和寄存器分析

为了进一步确定最终结构，还需要考虑硬件消耗情况，在输出结果符合要求的前提下，消耗较少加法器和寄存器为优。表3为2-7和3-6两种情况下的加法器个数和有效位数。

 

 

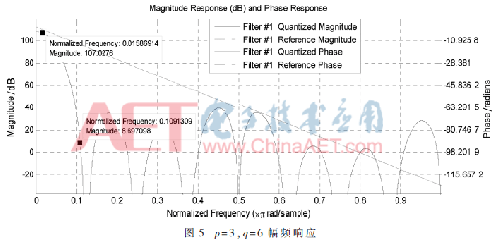
两种结构的衰减特性基本一样，字长也相同，只相差一个加法器。将上述两种结构通过SIMULINK仿真，查看结果发现，p=3，q=6结构与总的传输函数匹配效果更好，输出信噪比更高。所以最终选择p=3，q=6，其幅频响应如图5。

 

 

完成对上述两部分阶数和结构的选择后，将其级联，完成CIC滤波器整体设计。第一部分阶数为3阶，利用多相分解；第二部分阶数为6阶，选取传统递归结构，最终实现高频工作。

 

2 其他滤波器的设计

2.1 CIC补偿滤波器

完成CIC滤波器的设计后，观察其基带内的幅频响应，得到通带边缘处的衰减为0.2 dB。为使通带信号平坦，满足通带纹波小于0.01 dB的设计要求，需在CIC滤波器后加CIC补偿滤波器，对CIC滤波器输出信号的通带衰减进行补偿。同时，CIC补偿滤波器还兼顾2倍降采样的作用。

 

利用MATLAB中SIMULINK模型库中的CIC Compensator  Fliter，对CIC补偿滤波器进行设计。根据输入信号采样频率和降采样率，计算得：通带频率9 MHz，阻带频率11 MHz，滤波器结构选用直接型。

 

设计所得的CIC补偿滤波器阶数为72阶，消耗乘法器73个，加法器72个。

 

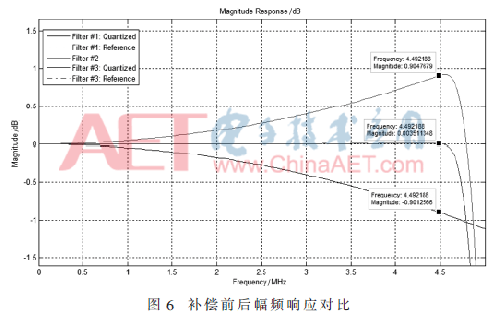
通过MATLAB编程得到补偿前后的滤波器幅频响应曲线如图6。

 

 

经过CIC补偿滤波器后，响应曲线变得非常平，带宽附近的通带衰减为0.003 5 dB，达到小于0.01 dB的设计要求。

 

 

2.2 半带滤波器

为达到阻带衰减要求，最后一级选用半带滤波器[5]。本次设计利用MATLAB中的“filter design”。采用“等纹波”法进行设计，结构上选取直接型结构。根据输入采样频率20 MHz，降采样率2，在滤波器设计界面中设置阻带衰减为105 dB，计算得到过渡带宽度为1 MHz。最终设计得到半带滤波器的幅频响应曲线如图7所示。本次设计消耗乘法器65个，加法器64个。

 

 

由图7可知，滤波器的通带和阻带衰减均满足设计要求。

 

3 仿真结果

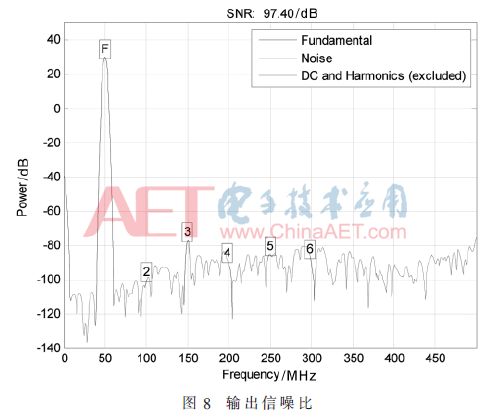
在SIMULINK Module中将上述每一子模块搭建完成后进行级联，输入一个幅度为0.67 V，频率为0.5 MHz的正弦波。将最后的输出数据(设为a)通过To Workspace导入到MATLAB中，在MATLAB命令行中执行snr（a），计算输出信号信噪比，得到整个ΣΔ模数转换器的输出信噪比为97.40 dB，如图8所示，计算得到分辨率为16位。

 

 

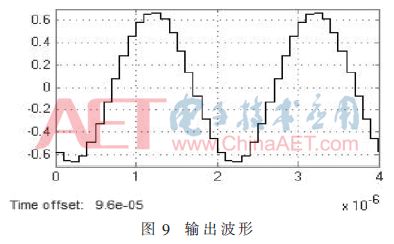
为进一步验证数字抽取滤波器的输出结果，使用示波器观察输出波形。选择SIMULINK中的scope模块，输入相应的时间范围，本次设置选择显示两个时间周期。得到输出波形如图9所示，可以看到输出维持了输入正弦信号的趋势。

 

 

4 结论

本论文以降低功耗为目的，对工作在高频信号下的数字抽取滤波器结构进行设计。利用多项分解优化了CIC滤波器结构，并搭建了四阶调制器，利用MATLAB软件对其进行功能仿真。最终仿真所得各项结果均满足设计要求。