推荐系统 - 1 - 相似度

         本总结是是个人为防止遗忘而作，不得转载和商用。

 

相似度/距离计算方法总结

         既然聚类思路的核心是度量样本间的内在相似性，那相似度/距离的计算方法是什么呢？

         首先先给出个汇总图，然后在解释，汇总图如下：

         解释：

                   闵可夫斯基距离/欧氏距离：

                            对于两个点(x1,y1)，(x2,y2)，他们的距离是((x2-x1)² + (y2-y1)²)^1/2

                            为了拓展为n维，就定义向量x=(x1,y1, z1, ...)，不过为了方便举例就用3维来说明吧：

                                     两个三维的点x=(x1,x2, x3)，y=(y1, y2, y3)

                            于是它们的距离就是((x1-y1)²+ (x2-y2)² + (x3-y3)²)^1/2

                            PS：这就是二范式||x -y||₂ ，即：里面都是平方，外面都是平方根。

                            那如果里面都是3次方，外面是3次方根呢？或者里面都是p次方，外面是p次方根呢？也可以吧，反正就是度量度量两点间的距离。

                            于是把上面的汇总下就是：闵可夫斯基距离/欧氏距离的公式。

                            PS：如果p=2时是欧氏距离，p为某一个值时是闵可夫斯基距离，p为∞时是切比雪夫距离。

                  杰卡德相似系数：

                            有时有这样的情况：A和B是两个集合。

                            比如：A喜欢看某些电影，B喜欢看某些电影。我们想度量A和B之间的相似度。

                            这时就用杰卡德相似系数了。

                            推荐系统可考虑选择这个。

                   余弦相似度：

                            如下图所示：

                           

                            有些时候会用A和B之间张成的的角的大小来度量两者的相似性

                            文本相似度可考虑选择这个。

                  Pearson相似系数：

                            就是求两个随机变量的相关系数，即：协方差除上标准差。

                            因为相关系数的绝对值小于等于1，cov(X, Y)可以认为是标准化的协方差，而协方差又是线性关系的一种度量。所以这个可以度量两者的相似性。

                   相对熵(K||L距离/散度)：

                            这个在最大熵模型中已经解释了，不懂的看我的总结。

                   Hellinger距离：

                            令α= 0的话，就有下面的推导

                           

                            令α= ±1时，这个就是K-L散度。

Jaccard相似度的由来

         记：R(u)是给用户u作出的推荐列表，而T(u)是用户在测试集上真正的行为列表。

         于是有如下准确率和召回率：

         而Jaccard相似度就是把准确率和召回率做了个合并，成为：

                  

         Jaccard系数特点和用途：

                   各个特征间是均一无权重的

                   网页去重/考试防作弊系统/论文抄袭检查

余弦相似度与Pearson相似系数：

                   首先，余弦相似度可以做如下变换：

                           

                   这时，如果令Pearson中的μx和μy都等于0的话，那Pearson相似系数的公式就是余弦相似度的公式。

                   所以Pearson相关系数即将x、y坐标向量各自平移到原点后的夹角余弦！

                   这即解释了为何文档间求距离使用夹角余弦——因为这一物理量表征了文档去均值化后的随机向量间相关系数。

 

         最后：

                   在实际应用中，根据情况选择一种距离求出后，对距离取分之一，就是相似度，即：距离和相似度互为倒数。

代码(源自邹博老师)

例子

         已知：

         某影院收集了N个用户对于M个电影的观影记录。每个用户一行，第i行记录形式为：

                   <用户ID>\t<电影1>;<电影2>;。。。。

                  如：

                            1347842  44

                            1347847  30;44

                            134790     28;30

                            ....

        已知莫愁的观影记录为：84,14, 90,91, 29, 21, 9, 44,24, 89, 8, 42, 41, 40,25, 37, 30, 16, 97, 52, 62,56,80, 83, 36,26, 73, 64, 32, 27, 67, 65, 79, 87, 17。

         求：

         找出与莫愁最匹配的前15名用户。

         解(其实更贴近的说法是思考过程)：

                   令A=莫愁的观影记录集合；B=某影院收集了N个用户对于M个电影的观影记录

                   1，第一步是想办法求出A与B的相似度。

                            而对比下上面那些相似度发现使用杰卡德相似度会十分方便，不过有没有其他相似度可以使用？

                           我们作如下思考：对于每一个用户，我们都可以为其创建一个默认的全为0的向量，向量的长度是电影数量M。然后对该向量做此操作：凡是用户看过的电影，向量中对应该电影的那个元素的值为1，反之为0。为了方便之后的说明，我们假定两个用户“莫愁”和“用户X”的电影向量M1和Mx如下：

                                              M1 =[0010100101101....0101010]_M

                                              Mx = [1001010010110....1011010]_M

                           这样看来，使用余弦相似度好像也不错。

                            而如果把M1和Mx的那些值看做是坐标点的话，就能使用欧氏距离。

                            所以说，在实践层面上面的相似度都是可以使用的。

                   2，在第一步中有：对每一个用户都存一个长度为M的向量。但有必要一定要存一个这么长的向量吗？还是向量M1和Mx：

                                     M1= [0010100101101....0101010]_M

                                     Mx= [1001010010110....1011010]_M

                            对余弦相似度来说M1^T·Mx和||M1||、||Mx||代表什么？

                            M1^T·Mx代表：

                                    

                            ||M1||代表：

                                     ，即莫愁看过的电影的数量。

                            ||Mx||同上。

                            而M1和Mx都是只有0和1两个元素的向量啊，如果M1的第i个元素和Mx的第i个元素不同时为1的话，M1^T·Mx = 0，反之M1^T·Mx = 1。

                            即：M1^T·Mx就是看看“莫愁”和“用户x”看过的电影中有多少个一样的！

                            于是，如果使用余弦相似度的话，我们就没必须把M1和Mx在程序中写出来然后再去做，只需要统计下相同的数目以及每个人看过几个电影就可以了。

                   因为本章仅仅总结相似度，所以这个题就到底为止了。

PS：电影见的相似度可以这么思考：   对于用户1，看过电影1,2,3，....   对于用户2，看过电影1,3,4，....   其他用户....   上面是用户对电影的数据，下面我们改变下统计方式，根据上面的数据统计出电影对用户的数据，即：   看过电影1的用户有：用户1，用户2， 用户5，....   其他电影....   然后把这个数据代入刚才的相似度计算中就可以了。

到底哪个相似度好啊

         看了上面的例子，相信你会想这个问题。

         在回答这个问题之前先看几幅图。

         下面几幅图是刚才例子中采取不同的标准求得的相似度的情况。

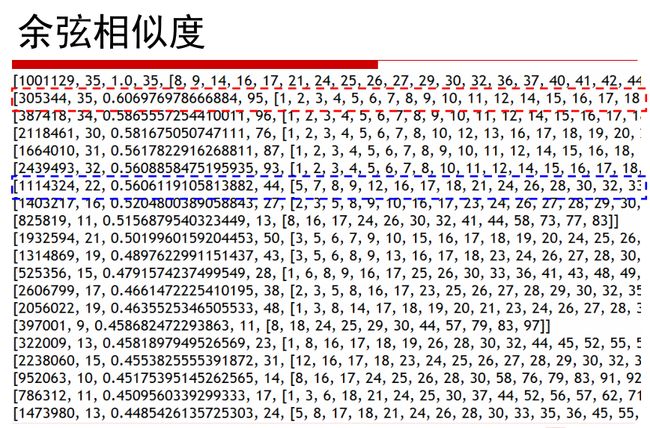
         第一列是用户ID，第二列是某用户看过的电影中与莫愁看过的电影相同的数目，第三列是相似度，越接近行首相似程度越高。

         第一行：“莫愁”和自己的相似度是1，排在行首。

         第二行：用户305344看了95个电影，然后这95个电影中正好包含了莫愁看的那35个。

         篮框行：用户1114324看了44个电影，然后这22个电影中正好包含了莫愁看的那35个。

         这样判断没问题。

         在余弦相似度中排在第七位的篮框行在这里排在了第二位，而刚才排在第二位的却排在了第三位，为什么呢？

         因为Jaccard是这么想：莫愁看了35个，用户1114324看了44个，他们中有22个相同的，这个22在35中占了比例很高，在44中占得比例也高，所以我认为1114324与莫愁最相似。

 

         所以，那种相似度都有它的解释，没有说哪个一定好哪个一定坏，这个最终还要看场合。