SLAM学习笔记2：Kalman Filter(卡尔曼滤波) 与Least Square(最小二乘法) 的比较

对于一个问题的解决，最根本在于怎样对它进行数学建模。对SLAM问题的建模，基本上是基于filter和graph两大类，今天整理了一下，对比两种模型的区别及共性。

主要参考这篇讲解：http://www.insidegnss.com/node/3445
以及《最优估计理论》刘胜，张红梅，科学出版社

---

Kalman filter和Least Square的目标都是误差最小化，Least Square是优化方法中的一种特殊情况，而卡尔曼滤波又是Least Square的一种特殊情况。
优化的目标是一个优化问题的关键，它决定了我们后续的算法选择。

常用的估计准则包括：
1. 无偏估计：即假设状态的估计值与真实值的平均值相等。
2. 最小二乘估计：不考虑数据的统计特性，如期望，方差等，直接用最小二乘法得到最优估计。
3. 误差方差最小：在满足最小二乘估计的同时，使得估计的误差方差最小。这一约束可以通过一系列等价的推导获得，前提是要事先知道测量数据噪声的方差。
简单来说就是，满足误差方差最小必满足误差平方和最小，反之不成立。而无偏估计是最基本假设。

由于最优估计里面变量比较多，自己看的时候基本上是长期保持懵逼态的，花了不少时间才理清楚。讲之前还是先明确几个概念吧，不分清楚后面基本就一锅粥了：
1. vi , 第i次测量时的噪声，测量噪声。
2. ei^ , 第i次测量时，测量值与估计值之差，测量误差。
3. J(X^) , ei^ 的平方和，最小二乘的最小化目标。
4. X~ , 真实值 X 与估计值 X^ 之差, 估计误差。
5. Var(X~) , 估计误差的方差，误差方差最小化的最小化目标。

---

古典最小二乘估计(Ordinary Least Square, OLS)

假如有一个系统状态X，无法直接观测，那么用其它方式获得它的观测值  Z ,  Z=[Z1,Z2,...,Zn] ，若观测值是状态值的线性函数，则有：

 Zi=HiX+Vi,i=1,2,...,n

Zi表示第i次测量得到的观测值， Hi表示第i次测量的观测模型， Vi表示第i次测量的误差。那么第i次测量的估计误差为：

 ei^=Zi−HiX^

于是m次测量的总误差为：

J(X^)=∑i=1m(Zi−HiX^)2=(Z−HX^)T(Z−HX^)

我们的目标是要求总误差的最小值，导数必为0：

∂J(X^)∂X^=0

得到的 X^LS 即是最小二乘估计值：

X^LS=(HTH)−1HTZ

此时估计误差为:

X~LS=X−X^LS=−(HTH)−1HTV

因为测量误差均值为0，所以估计误差的期望值为:

E(X~LS)=E[−(HTH)−1HTV]=−(HTH)−1HTE(V)=0

此时最小二乘估计为无偏估计，估计误差方差阵 Var(X^) 与估计量的均方误差阵 E[X−X^][X−X^]T 相等。

注意 J(X^LS) 与估计误差方差阵 Var(X~LS) 概念不同，最小二乘估计只保证测量值与估计值的平方和最小，不保证估计误差的方差最小。最小二乘估计不需要随机变量V的任何统计信息。

加权最小二乘估计(Weighted Least Square, WLS)
在古典最小二乘中，假设了每一次测量的权重相同，但事实上这样并不合理。假如一个估计值偏离真实值很远，那么它对估计结果的影响就应该被削弱，反之影响应该加强。加权最小二乘就是做这样的事。

加权最小二乘估计的误差平方和为：

JW(X^)=(Z−HX^)TW(Z−HX^)

同样要使这个误差平方和最小化：

∂JW(X^)∂X^=0

求得：

X^LSW=(HTWH)−1HTWZ

注意此时状态估计值 X^LSW 与权重矩阵W相关，不像古典最小二乘的 X^LS 为定值，即相当于W为新增的一个自由度，我们可以根据需要设定一个目标，在这条轴上找到指定的点满足目标。于是我们以估计误差方差最小化为目标。
通过一系列推导可以发现，当 W=R−1 时，最小二乘估计是缺少初值条件下的线性无偏最小方差估计，又称马尔科夫估计。

至此最小二乘估计所做的都是批处理（Batch），这样的方法需要耗费大量内存存储所有历史数据，并且计算量很大。而且这不符合动态系统状态估计的需要，每一次接受到新测量值的时候，需要整个模型重新计算，不能在线估计（Online）。

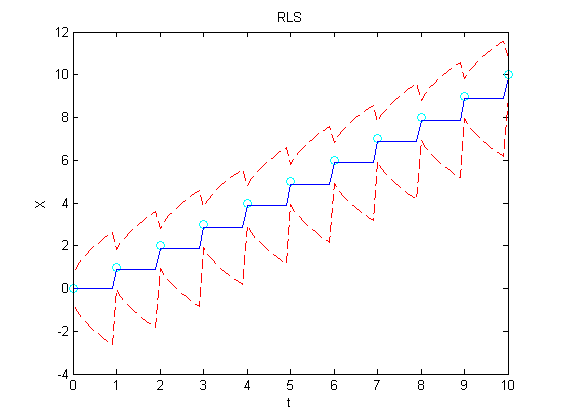
递推最小二乘估计(Recursive Least Square, RLS)
继续考虑n次测量：

 Zn=HnX+Vn

加权最小二乘估计为：

X^LSW(n)=[HTnRnHn]−1HTnR−1nHn

估计误差方差为：

Pk=E[X~LSW(n)X~TLSW(n)]

综合上面两式得：

X^LSW(n)=PnHTnR−1nZn

现在我们得到一个新测量：

zn+1=Hn+1X+vn+1

把新测量加入原来的大矩阵中得到：

Zn+1=Hn+1X+Vn+1

新的加权最小二乘估计为：

X^LSW(n+1)=[HTn+1Rn+1Hn+1]−1HTn+1R−1n+1Hn+1=Pn+1HTn+1R−1n+1Zn+1

要把新的测量噪声加入原本的测量噪声矩阵中，R矩阵应为对角矩阵：

R−1k+1=[R−1n00r−1n+1]

展开式子：

HTn+1R−1n+1Hn+1=[HTn,hTn+1][R−1n00r−1n+1][Hn,hn+1]=HTnR−1nHn+hTn+1r−1n+1hn+1

即：

P−1n+1=P−1n+hTn+1r−1n+1hn+1

最后推得：

Pn+1=Pn+PnhTn+1[hn+1PnhTn+1+rn+1]−1hn+1Pn

Kn+1=Pn+1hTn+1r−1n+1

X^LSW(n+1)=X^LSW(n)+Kn+1[zn+1−hn+1X^LSW(n)]

仔细观察发现，这货跟卡尔曼滤波的update式子就是一个意思啊。Weighted average of prediction and observation.

Graph SLAM
图优化SLAM就是基于权重最小二乘法的优化。所以每接收到一个新的观测值，必须记住还有information matrix需要更新。

Information matrix的更新方法：
首先明确information matrix是协方差矩阵的倒数。
1. 初始化时， I=0 。
2. 对于每一个输入观测值，计算协方差（根据经验）。
3. 求出协方差矩阵的倒数，即为信息 W ,
4. 计算输出误差，把它对输入求偏导，得Jacobian矩阵 J 。
5. 把信息W转换到误差空间 X=JTWJ
6. 设置 I=I+X
来源：http://www.triait.com/question/RGBD-SLAM-Compute-Information-Matrix/

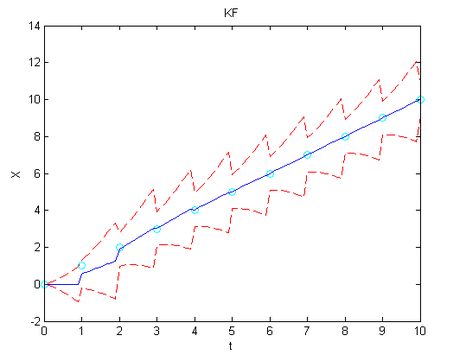
卡尔曼滤波(Kalman Filter)
与递归最小二乘相似，卡尔曼滤波加入了系统内部变化的考虑。即利用process model对系统在下一时刻的状态进行预测。
关于卡尔曼滤波的详细讲解，白巧克力亦唯心 大神已经讲得很详细了，请直接参看原blog:
http://blog.csdn.net/heyijia0327/article/details/17487467

---

总结一下， 它们之间的关系简而言之就是：
1. 古典最小二乘只最小化测量误差平方和 J(X^) 。
2. 权重最小二乘不仅最小化测量误差平方和 J(X^) ，还最小化估计误差方差阵 X~ 。
3. 递归最小二乘考虑动态测量，解决权重最小二乘每一次接收到新测量值时，需要全局更新的问题。
4. 卡尔曼滤波不仅考虑动态测量，还考虑系统内部的动态变化，加入Process model进行系统状态预测，并将预测值与测量值做权重和，使测量误差平方和 J(X^) 最小，估计误差方差阵 X~ 最小。

来源：在Quora上看到的关于kalman与RLS区别的讨论：
https://www.quora.com/How-does-a-Kalman-filter-differ-from-Recursive-Least-Squares

既然二者优化的变量相同，为何图优化结果大大优于滤波？
根据与群中大神@吴博-东北大学 的讨论，虽然卡尔曼滤波与图优化所优化的变量一致，但是二者针对的问题却不一致，模型也不一样。

以下是个人思考，希望各路大神指正：
卡尔曼滤波重视的是预测值与观测值的最优融合问题，即对观测数据的测量误差最小化，此时递推算法即可达到需求。

而图优化要做的事情是从全局上看问题，假如加入图内的nodes和edges未能形成闭环，那图优化的结果应与递归最小二乘结果相同，仅优化测量误差。可是一旦回环检测成功，最小化误差的约束除了 J(X^)，Var(X~) 最小以外，还需要增加 T1T2...Tn=I , 这是一条很强的约束，把之前每一个估计值中包含的误差都尽可能地做了消除。而此时如果还使用递归算法的话，旧的观测值与状态值都被融合进了最近的上一个状态中，误差无法再通过batch方法最小化。所以致力于单步误差最小化的卡尔曼滤波无法解决地图一致性（consistency）的问题。