R语言与回归分析学习笔记（bootstrap method）

           Bootstrap方法在之前的博文《R语言与点估计学习笔记（EM算法与Bootstrap法）》里有提到过，简而言之，bootstrap方法就是重抽样。为什么需要bootstrap方法呢？因为bootstrap方法使得我们无需分布理论的知识也可以进行假设检验，获得置信区间。当数据来自未知分布，或者存在严重异常点，又或者样本量过小，没有参数方法解决问题时，bootstrap方法将是一个很棒的方法。

        对于回归分析而言，bootstrap无疑对回归的正态性假设做了极大地放松，使得回归推断越来越好用，也更具有说服力。

        从博文《R语言与点估计学习笔记（EM算法与Bootstrap法）》里可以看到，对于参数统计，特别是在已知分布的参数估计，bootstrap并没有多大的意义，它的结果和矩估计或者极大似然估计的结果并没有多大的差别（如果有差别会令人觉得很奇怪，不是吗？）

        Boot包中提供了做bootstrap的两个十分好用的函数：boot（），boot.ci（）。两者的调用格式与参数说明如下：

        Boot（）函数：

boot(data, statistic, R, sim ="ordinary", stype = c("i", "f", "w"),

     strata= rep(1,n), L = NULL, m = 0, weights = NULL,

    ran.gen = function(d, p) d, mle = NULL, simple = FALSE, ...,

    parallel = c("no", "multicore", "snow"),

    ncpus = getOption("boot.ncpus", 1L), cl = NULL)

     参数说明：

Data：数据，可以是向量，矩阵，数据框

Statistic：统计量，如均值，中位数，回归参数，回归里的R^2等

R：调用统计量函数次数

         Boot（）的返回值：

T0:从原始数据中得到的k个统计量的观测值

T:一个R*K的矩阵

       Boot.ci（）函数：

boot.ci(boot.out, conf = 0.95, type = "all", 

        index = 1:min(2,length(boot.out$t0)), var.t0 = NULL, 

        var.t = NULL, t0 = NULL, t = NULL, L = NULL,

        h = function(t) t, hdot = function(t) rep(1,length(t)),

        hinv = function(t) t, ...)

        参数说明：

Boot.out（）：boot函数的返回值

Type：返回置信区间的类型，R中提供的有"norm" ,"basic", "stud","perc", "bca"

 

一、    对单个统计量使用bootstrap方法
          我们以R中的数据集women为例说明这个问题。数据集women列出了美国妇女的平均身高和体重。以体重为响应变量，身高为协变量进行回归，获取斜率项的95%置信区间。

     R可以通过以下代码告诉我们答案：

library(boot)
beta<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(fit$coef[2])
}
result<-boot(data=women,statistic=beta,R=500,formula=weight~height)
boot.ci(result)

       输出结果：

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Basedon 500 bootstrap replicates

CALL:

boot.ci(boot.out= result)

Intervals:

Level      Normal              Basic        

95%   ( 3.218, 3.686 )   ( 3.231,  3.704 ) 

Level     Percentile            BCa         

95%   ( 3.196, 3.669 )   ( 3.199,  3.675 ) 

Calculationsand Intervals on Original Scale

        他们与传统的估计差别大吗？我们来看看传统的区间估计：

confint(lm(weight~height,data=women))

       输出结果：

                 2.5 %     97.5 %

(Intercept) -100.342655 -74.690679

height        3.253112   3.646888

       可以看出，差别并不是很大，究其原因，无外乎正态性得到了很好的满足。我们看其qq图：

      很清楚也很显然。Shapiro检验也说明了这样一个事实：

        Shapiro-Wilk normality test

data:  women$weight

W = 0.9604,p-value = 0.6986

       我们在来看一个差别较大的例子：

.     考虑R中的数据集faithful。以waiting为响应变量，eruptions为协变量，建立简单回归模型y=α+βx+e。考虑β的95%置信区间。

      重复上面的步骤，R代码如下：

result<-boot(data=faithful,statistic=beta,R=500,formula=waiting~eruptions)
boot.ci(result)
confint(lm(waiting~eruptions,data=faithful))
qqPlot(lm(waiting~eruptions,data=faithful))

      输出结果：

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Based on 500bootstrap replicates

CALL :

boot.ci(boot.out= result)

Intervals :

Level      Normal              Basic        

95%   (10.08, 11.30 )   (10.06, 11.26 ) 

Level     Percentile            BCa         

95%   (10.20, 11.40 )   (10.13, 11.35 ) 

Calculationsand Intervals on Original Scale

Some BCaintervals may be unstable

      传统估计：

               2.5 %   97.5 %

(Intercept)31.20069 35.74810

eruptions   10.10996 11.34932

      差别有些大，我们来看看qq图：

      正态性不是很好，shapiro检验告诉我们几乎不可能认为是正态的。

        Shapiro-Wilk normality test

data:  faithful$waiting

W = 0.9221,p-value = 1.016e-10

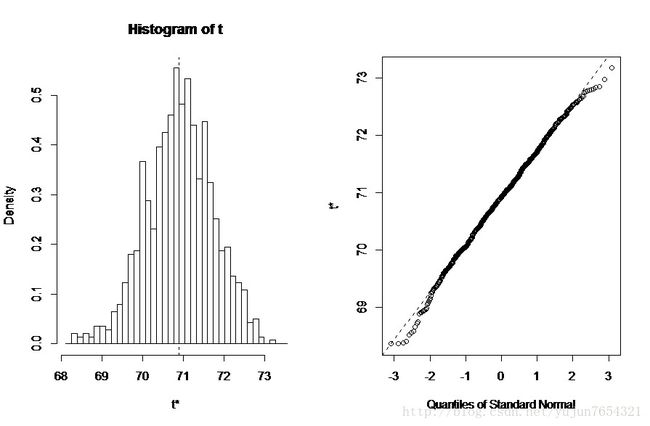
      观察下图，我们也可以看到waiting不服从正态分布，那么他的95%的置信区间可以通过以下代码获得：

mean1<-function(data,indices){
d<-data[indices,]
fit<-mean(d$waiting)
return(fit)
}
results<-boot(data=faithful,statistic=mean1,R=1000)
boot.ci(results)

       输出结果：

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Based on 1000bootstrap replicates

CALL :

boot.ci(boot.out= results)

Intervals :

Level      Normal              Basic        

95%   (69.28, 72.50 )   (69.31, 72.53 ) 

Level     Percentile            BCa         

95%   (69.26, 72.49 )   (69.10, 72.44 ) 

Calculationsand Intervals on Original Scale

        与传统方法比较

t.test(faithful$waiting)$conf.int

[1] 69.2741872.51994

        可见估计的稳健性。

二、   对多个统计量使用bootstrap方法

       我们考虑博文《R语言与回归分析学习笔记（应用回归小结）（1）》二中的例子，获取一个统计向量（四个回归系数）的95%置信区间。

       首先，创建一个返回回归系数向量的函数：

betas<-function(formula,data,indices){
d<-data[indices,]
fit<-lm(formula,data=d)
return(fit$coef)
}

       然后自助抽样500次：

results<-boot(data=states,statistic=betas,R=500,formula=Murder~.)
print(results)

       输出结果：

ORDINARYNONPARAMETRIC BOOTSTRAP

Call:

boot(data= states, statistic = betas, R = 500, formula = Murder ~  .)

BootstrapStatistics :

        original        bias      std. error

t1* 1.2345634112   8.969206e-01  5.305460e+00

t2* 0.0002236754   2.345369e-06 8.884204e-05

t3* 4.1428365903  -1.621533e-01  8.333313e-01

t4* 0.0000644247  -1.131896e-04  9.750587e-04

t5* 0.0005813055  -1.928938e-03  1.055004e-02

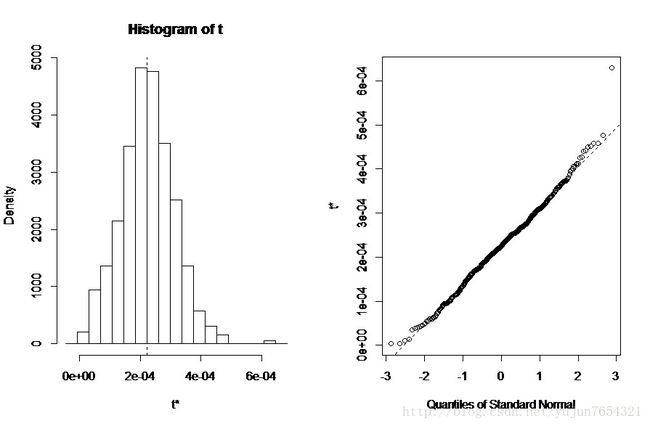
          当对多个统计量自助抽样时，需要添加一个索引参数，指明plot（），boot.ci()函数所分析对象。如下列代码用于绘制人口结果：

plot(results,index=2)

        输出结果：

       95%置信区间：

boot.ci(results,type="bca",index=2)
boot.ci(results,type="bca",index=3)
boot.ci(results,type="bca",index=4)

       输出结果：

>boot.ci(results,type="bca",index=2)

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Basedon 500 bootstrap replicates

CALL:

boot.ci(boot.out= results, type = "bca", index = 2)

Intervals:

Level       BCa         

95%   ( 0.0001, 0.0004 ) 

Calculationsand Intervals on Original Scale

 

>boot.ci(results,type="bca",index=3)

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Basedon 500 bootstrap replicates

CALL:

boot.ci(boot.out= results, type = "bca", index = 3)

Intervals:

Level       BCa         

95%   ( 2.284, 5.587 ) 

Calculationsand Intervals on Original Scale

SomeBCa intervals may be unstable

 

>boot.ci(results,type="bca",index=4)

BOOTSTRAPCONFIDENCE INTERVAL CALCULATIONS

Basedon 500 bootstrap replicates

CALL:

boot.ci(boot.out= results, type = "bca", index = 4)

Intervals:

Level       BCa         

95%   (-0.0022, 0.0016 ) 

Calculationsand Intervals on Original Scale

三、    残差法。

          Boot包中给出的办法都是使用成对的bootstrap。结果较为稳健。但我们也可以使用残差法对有固定水平的预测变量做估计。

          算法如下：

        1、 先由观测数据拟合回归模型

       2、 然后获得响应与残差

       3、 从拟合残差集合中有放回随机抽取得到bootstrap残差集合

       4、 生成一个伪数据集，对x回归伪数据集，获得bootstrap参数估计beta

       5、 重复多次，得到beta的经验分布，做推断或估计

         我以women数据集为例，利用残差法说明回归系数显著不为0.R代码如下：

lm.reg<-lm(weight~height,data=women)
y.fit<-predict(lm.reg)
y.res<-residuals(lm.reg)
y.bootstrap<-rep(1,15)
datap<-rep(0,100)
dataq<-rep(0,100)
for(pin 1:100){
for(iin 1:15){
res<-sample(y.res,1,replace=TRUE)
y.bootstrap[i]<-y.fit[i]+res
}
datap[p]<-lm(y.bootstrap~women$height)$coef[1]
dataq[p]<-lm(y.bootstrap~women$height)$coef[2]
}
ecdf(datap)
ecdf(dataq)

         输出的结果

ecdf(datap)#x[1:100]= -104.56, -99.192, -97.884,  ...,-75.389, -72.604

ecdf(dataq)#x[1:100]= 3.2271, 3.2588, 3.2845,  ...,  3.625, 3.7125

       显然结论是对的，其95%的置信区间使用分位数法有：

A<-ecdf(datap)
B<-ecdf(dataq)
quantile(A,probs=c(0.025,0.975))
quantile(B,probs=c(0.025,0.975))

        输出结果：

> quantile(A,probs=c(0.025,0.975))

    2.5%        97.5%

-96.95054    -75.22924

> quantile(B,probs=c(0.025,0.975))

   2.5%        97.5%

3.264777    3.595554

          这次介绍遗留了两个有价值的问题：1、初始样本多大？2、应该重复多少次？第一个问题，没有简单的答案，但有一点是肯定的，bootstrap不会提供比初始样本更多的信息，初始信息的收集仍旧十分重要。第二个问题在计算机资源普及的今天，多做一些没有太大的坏处，但是monte carlo方法及方差缩减技术将是你需要学习的。