什么是二叉堆/java实现

堆的定义

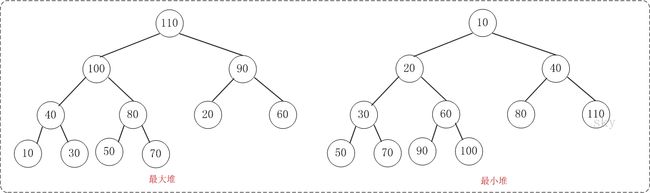
二叉堆是一种特殊的堆，可以看做是完全二叉树，它分为两个类型：

                    1.最大堆

                    2.最小堆

         什么是最大堆呢？就是父结点的键值总是大于或等于任何一个子节点的键值；

         什么是最小堆呢？父结点的键值总是小于或等于任何一个子节点的键值。

        其中二叉堆的根节点叫做堆顶。

        最大堆和最小堆的特点，决定了在最大堆的堆顶是整个堆中的最大元素；最小堆的堆顶是整个堆中的最小元素。

堆的自我调整

堆的构建其实就是依靠堆的自我调整，而堆的自我调整有如下几个操作：

  1.  添加节点

  2. 删除节点

  3. 构建二叉堆

接下来我们以最大堆为例，看看二叉堆是如何自我调整的。

• 添加节点

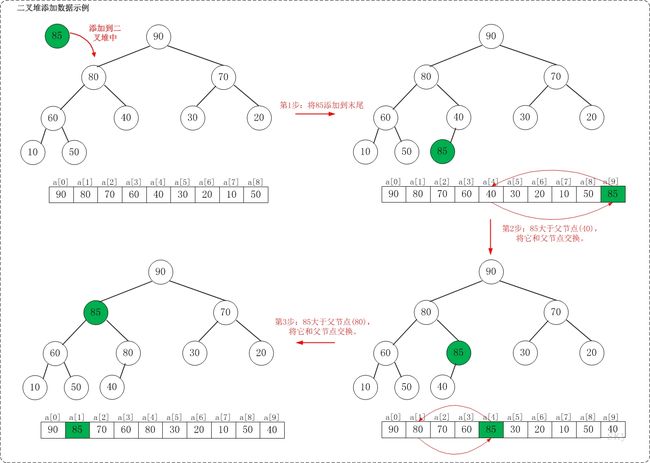
  假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85，需要执行的步骤如下：

如上图所示，当向最大堆中添加数据时：先将数据加入到最大堆的最后，然后将其与父节点做比较，如果大于父节点，就进行“上浮”操作，直到父节点比85大，上浮不动为止。将85添加到[90,80,70,60,40,30,20,10,50]中后，最大堆变成了[90,85,70,60,80,30,20,10,50,40]。

• 删除节点

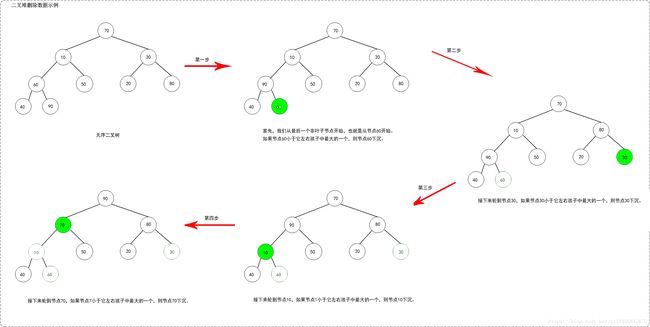
假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90，需要执行的步骤如下：

从[90,85,70,60,80,30,20,10,50,40]删除90之后，最大堆变成了[85,80,70,60,40,30,20,10,50]。如上图所示，当从最大堆中删除数据时：先删除该数据，然后用最大堆中最后一个的元素插入这个空位；接着，跟子节点中最大的数作比较，如果子节点大，则进行“下沉”操作，直到剩余的数据变成一个最大堆。

构建二叉堆

构建二叉堆，也就是把一个无序的完全二叉树调整为二叉堆，本质上就是让所有非叶子节点依次下沉。我们举一个无序完全二叉树的例子：

堆代码的实现

在实现代码之前，我们首先要明白

• 父节点与子节点的关系
  • 假设"第一个元素"在数组中的索引为 0 的话，则父节点和子节点的位置关系如下：
    • (01) 索引为i的左孩子的索引是 (2*i+1);
    • (02) 索引为i的右孩子的索引是 (2*i+2);
    • (03) 索引为i的父结点的索引是 floor((i-1)/2);
• 代码实现

  package Algorithm;
  
  import java.util.Arrays;
  
  /**
   * 二叉堆的代码实现
   */
  public class TwoForkPile {
      public static void main(String[] args) {
          int[] array = new int[] {1,3,2,6,5,7,8,9,10,0};
          upAdjust(array);
          System.out.println(Arrays.toString(array));
          array = new int[] {7,1,3,10,5,2,8,9,6};
          buildHeap(array);
          System.out.println(Arrays.toString(array));
      }
  
      /**
       * 构建二叉堆
       * @param array
       */
      private static void buildHeap(int[] array) {
          // 从最后一个非叶子节点开始，依次下沉调整
          for (int i = (array.length -2 )/ 2; i >= 0; i--) {
              downAdjust(array, i, array.length);
          }
      }
  
      /**
       * 下沉操作
       * @param array
       * @param parentIndex
       * @param length
       */
      private static void downAdjust(int[] array, int parentIndex, int length) {
          // temp保存父节点值，用于最后的赋值
          int temp = array[parentIndex];
          int childIndex = 2 * parentIndex + 1;
          while (childIndex < length) {
              // 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
              if (childIndex + 1 < length && array[childIndex + 1] > array[childIndex]) {
                  childIndex++;
              }
              // 如果父节点大于任何一个孩子的值，直接跳出
              if (temp >= array[childIndex]){
                  break;
              }
              //无需真正交换，单向赋值即可
              array[parentIndex] = array[childIndex];
              parentIndex = childIndex;
              childIndex = 2 * childIndex + 1;
          }
          array[parentIndex] = temp;
      }
  
      /**
       * 上浮操作
       * （增加节点）
       * @param array
       */
      private static void upAdjust(int[] array) {
          int childIndex = array.length-1;            //最后一个叶子元素
          int parentIndex = (childIndex - 1) / 2;     //最后一个非叶子的父节点
  
          int temp = array[childIndex];
          while(childIndex > 0 && temp > array[parentIndex]){
              array[childIndex] = array[parentIndex];
              childIndex = parentIndex;
              parentIndex = (parentIndex-1) / 2;
          }
          array[childIndex] = temp;
      }
  }
  

  参考文献

• 二叉堆（一）之图文解析和C语言的实现（链接地址：https://www.cnblogs.com/skywang12345/p/3610187.html）