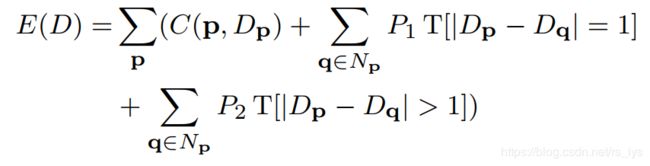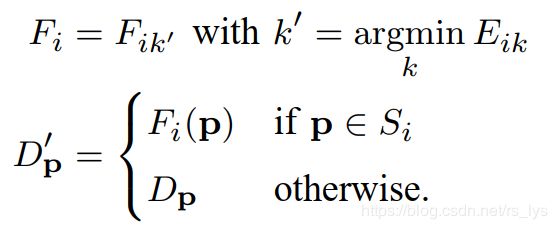【码上实战】【立体匹配系列】经典SGM：（7）弱纹理优化

欢迎收看长篇小说SGM第七章：弱纹理优化

码上教学系列

【码上实战】【立体匹配系列】经典SGM：（1）框架与类设计
【码上实战】【立体匹配系列】经典SGM：（2）代价计算
【码上实战】【立体匹配系列】经典SGM：（3）代价聚合
【码上实战】【立体匹配系列】经典SGM：（4）代价聚合2
【码上实战】【立体匹配系列】经典SGM：（5）视差优化
【码上实战】【立体匹配系列】经典SGM：（6）视差填充
【码上实战】【立体匹配系列】经典SGM：（7）弱纹理优化

代码已同步于Github开源项目：Github/GemiGlobalMatching

如前所述，SGM是一个优化的算法，源自两篇优秀的论文，作者Hirschmüller在2005年于TOP期刊PAMI上第一次发表SGM算法，又在2008年的顶会CVPR上再次发表，而CVPR上发表的和此前PAMI上的区别就在于增加了很多后处理步骤，博主自第五篇开始介绍的内容都来自于2008年的论文。很惭愧，博主自2014年开始接触SGM，开始并没有有完全读懂，后处理部分只是选择性的实现几项并再未静下心来认真阅读原文，直至今日，才对2008年的论文有一个完整的了解，感觉再次收货良多，如重拾旧友，倍感亲切。

本篇所介绍的内容是SGM后处理的其中一步：弱纹理区视差优化。如不出意外的话，本篇是手把手SGM教学的最后一篇，至此，原文中的所有模块都实现完成。当然，博主也不打算立Flag说肯定是最后一篇，万一后面心血来潮做一个额外的补充岂不是打脸。

【博主最近实在太忙，所以没时间写代码，但是手实在痒，所以决定先把理论讲一讲，后面再补代码】

三个假设

在弱纹理优化之前，作者提出三个假设，这三个假设至关重要，它是优化方法的理论依据，我们来看看原文如何描述：

1. Discontinuities in the disparity image do not occur within untextured areas.
2. On the same physical surface as the untextured area is also some texture visible.
3. The surface of the untextured area can be approximated by a plane.

我来翻译一下：

• 1）弱纹理区域不存在视差非连续。
• 2）弱纹理区域内应该存在一些可见的纹理。
• 3）弱纹理区所表示的表面能够用一个平面近似。

我将untextured翻译成弱纹理而非无纹理，我想作者讨论的应该是弱纹理，而无纹理是属于弱纹理的极端情况。

我们来逐个分析这三点假设，

1）弱纹理区域不存在视差非连续。

此假设在多数情况下成立，视差非连续往往会存在图像亮度的变化，比如前景和背景会因为离相机的距离不同而导致辐射强度不同，在图像上表现出亮度的差异，有了亮度的明显差异就不再属于弱纹理的范畴（弱纹理就是因为亮度差异太小而无法区分）。因此弱纹理区域内可以假设视差都是连续的。
【图】
但少数情况此假设会失效，有些情况前背景确实在图像上是同一亮度值，比如前后两块白墙，就可能在图像上都是无法区分的白色，这属于少数情况。
【图】
作者在此建立多数情况成立的假设，显然是无意提出适用于所有情况的完美解决方案，难度确实太大，而适应多数情况的解决方案是更合理且有效的。

2）弱纹理区域内应该存在一些可见的纹理。

此假设是必要假设，原因很简单，弱纹理区内若完全无纹理，则不可能估计正确视差，譬如左右视图上同一块区域都是全黑或者全白，实在想不出有什么办法可以正确估计视差。

这个假设很关键，弱纹理区域内有一些可见纹理所表达的背后含义是：可见纹理像素可以正确的计算出视差，从而为区域内其他像素的视差计算提供重要信息，这也是文章中弱纹理视差优化的前提，后面我们细说。

3）弱纹理区所表示的表面能够用一个平面近似。

此假设是三个中最弱的假设，该假设的理由是：非平面的表面往往会在图像上表现出亮度的变化。这个理由不一定成立，空间中的一个圆柱面也可能在图像上表现成连续的弱纹理块。但该假设也有很多正确的场景，比如多数结构化场景中，墙面、地面等都都是平面，在图像上常常表现成一大块弱纹理区域，符合该假设。

综上所述，三个假设所针对的是：空间中的平面在图像上呈现出一块亮度一致的弱纹理区域的情况。如果符合此种情况，则可基于上述三个假设采用文章中的优化方法来优化。

亮度一致性分割

弱纹理区视差优化的第一步是检测弱纹理区。弱纹理区的一大特征就是在图像上色彩（亮度）及其相近。

SGM作者采用Mean-Shift分割算法对影像进行分割，Mean-Shift是非常出名的图像分割算法，它的原理博主就不细说了，简单的说它把颜色相近的区域划分为同一子块，从而把图像分割成多个子块的算法。博主贴一些Mean-Shift的实验图同学们感受一下（来自opencv的meash-shift算法）：

看到这里，大家可能会心里有点想法了，肯定是利用块内的好结果来修正差结果，就是不知道具体细节，那我们再继续往下分析。

首先，我们把分割结果每一块记为$S_i$($i=0...N$，$N$为分割快数)，把面积小于阈值（论文推荐值：100）的块丢掉，因为小面积的弱纹理区域SGM处理的还不错，不需要做优化。

其次，我们把每一块内的视差连通块，记为$S_{ik}$，表示图像块$S_i$内的第$k$块视差连通块。

不得不说，SGM对这种极弱纹理的数据结果真是太辣了。当然其他算法也不会太好，毕竟是立体匹配的疑难杂症。如果能处理好弱纹理，对室内的图像三维重建是不错的突破。现在室内都是Kinnect等主动式深度采集设备的天下。

有同学就举手问：要是图像块内完全没有视差块呢？这就要回到我们前面的假设2了：弱纹理区域内应该存在一些可见的纹理。有可见纹理SGM便能在纹理位置估计出有效视差。什么？完全没有？对不起，你破坏了我的假设，我不考虑，就是这么傲娇！

好了，标记工作完成，接下来就是对弱纹理区域做视差优化了。

弱纹理区视差优化

图像分成一块块了，每块内的视差也分成块了，接下来该怎么做？

轮到我们的假设3登场：弱纹理区所表示的表面能够用一个平面近似。

所以我们一个图像块就是一个平面对不对，一个平面的视差也是一个平面（这简单的推理留给大家）。所以思路就是：寻找图像块$S_i$内的最优视差平面，然后基于平面方程计算块内无效像素的视差。

而寻找块$S_i$内的最优视差平面的方法就是对块内的所有视差块都分别拟合一个平面$F_{ik}$，然后基于每个$F_{ik}$计算块内所有像素的视差，之后计算块$S_i$的能量值$E_{ik}$，取能量值最小的平面$F_{ik}$为最优视差平面。
【能量值计算公式】

计算出块$S_i$的最优视差平面后，便可通过平面公式计算出块内非遮挡无效像素的视差值。非遮挡像素的判断规则上一篇博客有讲解。最后的优化公式如下：

实验结果

【代码暂缺，实验结果暂缺，后补】

理论恒叨系列

【理论恒叨】【立体匹配系列】经典SGM：（1）匹配代价计算之互信息（MI）
【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换
【理论恒叨】【立体匹配系列】经典SGM：（3）代价聚合（Cost Aggregation）
【理论恒叨】【立体匹配系列】经典SGM：（4）视差计算、视差优化

博主简介：
Ethan Li 李迎松
武汉大学 摄影测量与遥感专业博士

主方向立体匹配、三维重建

2019年获测绘科技进步一等奖（省部级）

爱三维，爱分享，爱开源
GitHub： https://github.com/ethan-li-coding
邮箱：[email protected]

个人微信：

欢迎交流！

喜欢博主的文章不妨关注一下博主的博客，感谢！
博客主页：https://blog.csdn.net/rs_lys